Difference between revisions of "Aufgaben:Exercise 5.5: Multi-User Interference"
m (Text replacement - "rms value" to "standard deviation") |
|||
| (5 intermediate revisions by 2 users not shown) | |||
| Line 10: | Line 10: | ||
* The bit error probability without interfering subscribers in the same frequency band is: | * The bit error probability without interfering subscribers in the same frequency band is: | ||
:$$p_{\rm B} = {\rm Q} \left ( \sqrt{ {2\cdot E_{\rm B}}/{N_{\rm 0}}}\right ) \approx {\rm Q} \left ( \sqrt{2 \cdot 3.162}\right ) = {\rm Q} \left ( 2.515 \right ) \approx 6 \cdot 10^{-3} \hspace{0.05cm}.$$ | :$$p_{\rm B} = {\rm Q} \left ( \sqrt{ {2\cdot E_{\rm B}}/{N_{\rm 0}}}\right ) \approx {\rm Q} \left ( \sqrt{2 \cdot 3.162}\right ) = {\rm Q} \left ( 2.515 \right ) \approx 6 \cdot 10^{-3} \hspace{0.05cm}.$$ | ||
| − | * | + | * The value of the signal at sampling time, without noise or interfering subscribers, is equal to $±s_0$ ("Nyquist system"). As a result, the bit error probability for noise standard deviation $σ_d$ before the decision stage $($ originating from the AWGN noise$)$ can be stated as follows: |
:$$p_{\rm B} = {\rm Q} \left ( {s_0}/{\sigma_d}\right ) \hspace{0.05cm}.$$ | :$$p_{\rm B} = {\rm Q} \left ( {s_0}/{\sigma_d}\right ) \hspace{0.05cm}.$$ | ||
| Line 40: | Line 40: | ||
*The exercise belongs to the chapter [[Modulation_Methods/Error_Probability_of_Direct-Sequence_Spread_Spectrum_Modulation|Error Probability of Direct-Sequence Spread Spectrum Modulation]]. | *The exercise belongs to the chapter [[Modulation_Methods/Error_Probability_of_Direct-Sequence_Spread_Spectrum_Modulation|Error Probability of Direct-Sequence Spread Spectrum Modulation]]. | ||
*Reference is made in particular to the section [[Modulation_Methods/Error_Probability_of_Direct-Sequence_Spread_Spectrum_Modulation#Two_users_with_M-sequence_spreading|Two users with M-sequence spreading]]. | *Reference is made in particular to the section [[Modulation_Methods/Error_Probability_of_Direct-Sequence_Spread_Spectrum_Modulation#Two_users_with_M-sequence_spreading|Two users with M-sequence spreading]]. | ||
| − | *For the so-called [[Applets:Complementary_Gaussian_Error_Functions|Q-function]], the following approximations can be assumed: | + | *For the so-called [[Applets:Complementary_Gaussian_Error_Functions|Q-function]], the following approximations can be assumed: |
:$$ {\rm Q} (2) \approx 0.02275, \hspace{0.2cm}{\rm Q} (3) \approx 0.00135, \hspace{0.2cm}{\rm Q} (5) \approx 2.45 \cdot 10^{-7} \hspace{0.05cm}.$$ | :$$ {\rm Q} (2) \approx 0.02275, \hspace{0.2cm}{\rm Q} (3) \approx 0.00135, \hspace{0.2cm}{\rm Q} (5) \approx 2.45 \cdot 10^{-7} \hspace{0.05cm}.$$ | ||
| Line 47: | Line 47: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {What is the (normalized) noise | + | {What is the (normalized) noise standard deviation at the decision maker? |
|type="{}"} | |type="{}"} | ||
$σ_d/s_0 \ = \ $ { 0.4 3% } | $σ_d/s_0 \ = \ $ { 0.4 3% } | ||
| Line 69: | Line 69: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' From the two equations given above, it follows directly: | + | '''(1)''' From the two equations given above, it follows directly: |
:$$p_{\rm B} = {\rm Q}(2.515) = {\rm Q}({s_0}/{\sigma_d}) \hspace{0.3cm}\Rightarrow\hspace{0.3cm} \frac{\sigma_d}{s_0} = \frac{1}{2.515} = 0.398 \hspace{0.15cm}\underline {\approx 0.4} \hspace{0.05cm}.$$ | :$$p_{\rm B} = {\rm Q}(2.515) = {\rm Q}({s_0}/{\sigma_d}) \hspace{0.3cm}\Rightarrow\hspace{0.3cm} \frac{\sigma_d}{s_0} = \frac{1}{2.515} = 0.398 \hspace{0.15cm}\underline {\approx 0.4} \hspace{0.05cm}.$$ | ||
| − | *However, one could also calculate this quantity using the more general equation | + | *However, one could also calculate this quantity using the more general equation |
| − | :$$ \sigma_d^2 = \frac{N_0}{2 }\cdot\int^{+\infty}_{-\infty} |H_{\rm I}(f) |^2 \,\,{\rm d} {\it f}\hspace{0.05cm} = \frac{N_0}{2 }\cdot\int^{+\infty}_{-\infty}{\rm | + | :$$ \sigma_d^2 = \frac{N_0}{2 }\cdot\int^{+\infty}_{-\infty} |H_{\rm I}(f) |^2 \,\,{\rm d} {\it f}\hspace{0.05cm} = \frac{N_0}{2 }\cdot\int^{+\infty}_{-\infty}{\rm sinc}^2(f T)\,\,{\rm d} {\it f} = \frac{N_0}{2T } \hspace{0.05cm}.$$ |
| − | : Here $H_{\rm I}(f)$ describes the integrator in the frequency domain. | + | : Here $H_{\rm I}(f)$ describes the integrator in the frequency domain. |
| − | *With $E_{\rm B}= s_0^2 · T$ the same result is obtained: | + | *With $E_{\rm B}= s_0^2 · T$ the same result is obtained: |
:$$\frac{\sigma_d^2}{s_0^2} = \frac{N_0}{2 \cdot s_0^2 \cdot T } = \frac{N_0}{2 E_{\rm B} } = \frac{0.316}{2 } = 0.158\hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\sigma_d}/{s_0} = 0.398 \approx 0.4 \hspace{0.05cm}.$$ | :$$\frac{\sigma_d^2}{s_0^2} = \frac{N_0}{2 \cdot s_0^2 \cdot T } = \frac{N_0}{2 E_{\rm B} } = \frac{0.316}{2 } = 0.158\hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\sigma_d}/{s_0} = 0.398 \approx 0.4 \hspace{0.05cm}.$$ | ||
| − | '''(2)''' If the interfering participant uses the same M-sequence $(45)$ as the considered user, <br> then the (normalized) detection | + | '''(2)''' If the interfering participant uses the same M-sequence $(45)$ as the considered user, <br> then the (normalized) detection samples (without noise) are equal to $+2$ $($at $25\%)$, $-2$ $($at $25\%)$ and $0$ $($at $50\%)$. |
| − | *When $d(νT) = ±2$, the error probability for the considered user is significantly reduced. In this case, both users transmit the same bit $($"$+1$" or "$-1$"$)$ and the distance from the threshold is doubled: | + | *When $d(νT) = ±2$, the error probability for the considered user is significantly reduced. |
| + | *In this case, both users transmit the same bit $($"$+1$" or "$-1$"$)$ and the distance from the threshold is doubled: | ||
:$$ p_{\rm B}\,\,\big [{\rm if}\,\, d (\nu T) = \pm 2s_0 \big ] = {\rm Q} \left ( 2 \cdot 2.515 \right ) = {\rm Q} \left ( 5.03 \right ) \approx 2.45 \cdot 10^{-7} \approx 0 \hspace{0.05cm}.$$ | :$$ p_{\rm B}\,\,\big [{\rm if}\,\, d (\nu T) = \pm 2s_0 \big ] = {\rm Q} \left ( 2 \cdot 2.515 \right ) = {\rm Q} \left ( 5.03 \right ) \approx 2.45 \cdot 10^{-7} \approx 0 \hspace{0.05cm}.$$ | ||
| − | *On the other hand, if $d(νT) = 0$ (for example, if $a_\text{1(s)} = +1$ and $a_\text{1(i)} = -1$ holds or vice versa), the signals cancel completely and we obtain | + | *On the other hand, if $d(νT) = 0$ (for example, if $a_\text{1(s)} = +1$ and $a_\text{1(i)} = -1$ holds or vice versa), the signals cancel completely and we obtain |
| − | :$$p_{\rm B} | + | :$$p_{\rm B}\big[{\rm if}\,\, d (\nu T) = 0 \big] = {\rm Q} \left ( 0 \right ) = 0.5 \hspace{0.05cm}.$$ |
| − | *Averaging over these two equally probable possibilities, we thus obtain for the mean bit error probability: | + | *Averaging over these two equally probable possibilities, we thus obtain for the mean bit error probability: |
:$$p_{\rm B}= 0.5 \cdot 2.45 \cdot 10^{-7}+ 0.5 \cdot 0.5 \hspace{0.15cm}\underline {\approx 25\%} \hspace{0.05cm}.$$ | :$$p_{\rm B}= 0.5 \cdot 2.45 \cdot 10^{-7}+ 0.5 \cdot 0.5 \hspace{0.15cm}\underline {\approx 25\%} \hspace{0.05cm}.$$ | ||
| − | '''(3)''' We first consider only the useful part ⇒ $n(t) = 0$, restricting ourselves to the first data symbol and assuming the coefficient $a_\text{1(s)} = +1$. | + | '''(3)''' We first consider only the useful part ⇒ $n(t) = 0$, restricting ourselves to the first data symbol and assuming the coefficient $a_\text{1(s)} = +1$. |
*Then within this data bit $s(t) = c_{45}(t)$ holds. | *Then within this data bit $s(t) = c_{45}(t)$ holds. | ||
| − | *If the coefficient $a_\text{1(i)} $ of the interfering participant is also $+1$, then for the signals specified in front in the time interval from $0$ to $T$ we obtain: | + | *If the coefficient $a_\text{1(i)} $ of the interfering participant is also $+1$, then for the signals specified in front in the time interval from $0$ to $T$ we obtain: |
:$$ r(t) = c_{45}(t) + c_{75}(t)\hspace{0.05cm},$$ | :$$ r(t) = c_{45}(t) + c_{75}(t)\hspace{0.05cm},$$ | ||
:$$b(t) = r(t) \cdot c_{45}(t) = \left [c_{45}(t) + c_{75}(t) \right ] \cdot c_{45}(t) = 1+ c_{45}(t) \cdot c_{75}(t) \hspace{0.05cm},$$ | :$$b(t) = r(t) \cdot c_{45}(t) = \left [c_{45}(t) + c_{75}(t) \right ] \cdot c_{45}(t) = 1+ c_{45}(t) \cdot c_{75}(t) \hspace{0.05cm},$$ | ||
:$$ d (T) = \frac{1}{T} \cdot \int_{0 }^{ T} b (t )\hspace{0.1cm} {\rm d}t = 1 + {\it \varphi}_{45,\hspace{0.05cm}75}(\lambda = 0) \hspace{0.05cm}.$$ | :$$ d (T) = \frac{1}{T} \cdot \int_{0 }^{ T} b (t )\hspace{0.1cm} {\rm d}t = 1 + {\it \varphi}_{45,\hspace{0.05cm}75}(\lambda = 0) \hspace{0.05cm}.$$ | ||
| − | *Here, $φ_\text{45, 75}(τ)$ denotes the PCCF between the spreading sequences with octal identifiers $(45)$ and $(75)$, which can be found in the table on the data page. | + | *Here, $φ_\text{45, 75}(τ)$ denotes the PCCF between the spreading sequences with octal identifiers $(45)$ and $(75)$, which can be found in the table on the data page. |
| − | + | *Correspondingly, for the detection sample without noise, given $a_\text{1(s)} = +1$ and $a_\text{1(i)} =-1$: | |
| − | *Correspondingly, for the detection | ||
:$$d (T) = 1 - {\it \varphi}_{45,\hspace{0.05cm}75}(\lambda = 0) \hspace{0.05cm}.$$ | :$$d (T) = 1 - {\it \varphi}_{45,\hspace{0.05cm}75}(\lambda = 0) \hspace{0.05cm}.$$ | ||
| − | *For symmetry reasons, the coefficients $a_\text{1(s)} = -1$, $a_\text{1(i)} = -1$ as well as $a_\text{1(s)} = -1$, $a_\text{1(i)} = +1$ provide exactly the same contributions for the bit error probability as $a_\text{1(s)} = +1$, $a_\text{1(i)} = +1$ and $a_{1(s)} = +1$, $a_{1(i)} = | + | *For symmetry reasons, the coefficients $a_\text{1(s)} = -1$, $a_\text{1(i)} = -1$ as well as $a_\text{1(s)} = -1$, $a_\text{1(i)} = +1$ provide exactly the same contributions for the bit error probability as $a_\text{1(s)} = +1$, $a_\text{1(i)} = +1$ and $a_{1(s)} = +1$, $a_{1(i)} = -1$ respectively, if we also consider the AWGN noise. |
| − | *Thus, using the result of subtask '''(1)''' and with $φ_\text{45, 75}(λ = 0) = 7/31$, we obtain approximately: | + | *Thus, using the result of subtask '''(1)''' and with $φ_\text{45, 75}(λ = 0) = 7/31$, we obtain approximately: |
:$$p_{\rm B} = \frac{1}{2} \cdot {\rm Q} \left ( \frac{1+ 7/31}{0.4} \right ) + \frac{1}{2} \cdot {\rm Q} \left ( \frac{1- 7/31}{0.4} \right ) = \frac{1}{2} \cdot {\rm Q} \left ( \frac{1.225}{0.4} \right ) + \frac{1}{2} \cdot {\rm Q} \left ( \frac{0.775}{0.4} \right ) = \frac{1}{2} \cdot {\rm Q} \left ( 3.06 \right ) + \frac{1}{2} \cdot {\rm Q} \left ( 1.94 \right )$$ | :$$p_{\rm B} = \frac{1}{2} \cdot {\rm Q} \left ( \frac{1+ 7/31}{0.4} \right ) + \frac{1}{2} \cdot {\rm Q} \left ( \frac{1- 7/31}{0.4} \right ) = \frac{1}{2} \cdot {\rm Q} \left ( \frac{1.225}{0.4} \right ) + \frac{1}{2} \cdot {\rm Q} \left ( \frac{0.775}{0.4} \right ) = \frac{1}{2} \cdot {\rm Q} \left ( 3.06 \right ) + \frac{1}{2} \cdot {\rm Q} \left ( 1.94 \right )$$ | ||
:$$ \Rightarrow \hspace{0.3cm} p_{\rm B}\approx \frac{1}{2} \cdot \left [{\rm Q} \left ( 3 \right ) + {\rm Q} \left ( 2 \right ) \right ] = \frac{1}{2} \cdot \left [0.00135 + 0.02275 \right ] \hspace{0.15cm}\underline {= 1.2\%}\hspace{0.05cm}.$$ | :$$ \Rightarrow \hspace{0.3cm} p_{\rm B}\approx \frac{1}{2} \cdot \left [{\rm Q} \left ( 3 \right ) + {\rm Q} \left ( 2 \right ) \right ] = \frac{1}{2} \cdot \left [0.00135 + 0.02275 \right ] \hspace{0.15cm}\underline {= 1.2\%}\hspace{0.05cm}.$$ | ||
| − | '''(4)''' Possible solutions are <u>2 and 3</u>: | + | |
| + | '''(4)''' Possible solutions are <u>2 and 3</u>: | ||
* The PCCF value $φ_\text{45, 57}(λ = 0)$ is only $1/31$ in magnitude and thus the error probability is only slightly larger than $0.6\%$. | * The PCCF value $φ_\text{45, 57}(λ = 0)$ is only $1/31$ in magnitude and thus the error probability is only slightly larger than $0.6\%$. | ||
| − | *In contrast, the sequence with octal identifiers $(67)$ leads to the same PCCF as sequence $(75)$. | + | *In contrast, the sequence with octal identifiers $(67)$ leads to the same PCCF as sequence $(75)$. |
| − | *Without interfering participants, the following applies according to the data sheet: $p_{\rm B} = 0.6\%$. | + | *Without interfering participants, the following applies according to the data sheet: $p_{\rm B} = 0.6\%$. |
| − | *With interference, this value cannot be undercut ⇒ solution 1 is not possible. | + | *With interference, this value cannot be undercut ⇒ solution 1 is not possible. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 12:11, 17 February 2022
We consider "Direct-Sequence Spread Spectrum Modulation" with the following parameters:
- The spreading is done with the M-sequence $(45)_{\rm oct}$, starting from the degree $G = 5$. The period length is thus
- $$P = 2^5 –1 = 31.$$
- The AWGN parameter is set as $10 · \lg \ (E_{\rm B}/N_0) = 5 \ \rm dB$ ⇒ $E_{\rm B}/N_0 = 3.162 = 1/0.316$.
- The bit error probability without interfering subscribers in the same frequency band is:
- $$p_{\rm B} = {\rm Q} \left ( \sqrt{ {2\cdot E_{\rm B}}/{N_{\rm 0}}}\right ) \approx {\rm Q} \left ( \sqrt{2 \cdot 3.162}\right ) = {\rm Q} \left ( 2.515 \right ) \approx 6 \cdot 10^{-3} \hspace{0.05cm}.$$
- The value of the signal at sampling time, without noise or interfering subscribers, is equal to $±s_0$ ("Nyquist system"). As a result, the bit error probability for noise standard deviation $σ_d$ before the decision stage $($ originating from the AWGN noise$)$ can be stated as follows:
- $$p_{\rm B} = {\rm Q} \left ( {s_0}/{\sigma_d}\right ) \hspace{0.05cm}.$$
In this exercise, we want to investigate how the bit error probability is changed by an additional participant.
- The possible spreading sequences of the interfering participant are also defined by $P = 31$.
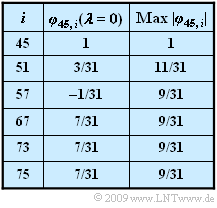
- The PN generators with octal identifiers $(45)$, $(51)$, $(57)$, $(67)$, $(73)$ and $(75)$ are available.
- In the first column of the table the PCCF values for $λ = 0$ are given, furthermore also the respective maximum value for another initial phase:
- $$ {\rm Max}\,\,|{\it \varphi}_{45,\hspace{0.05cm}i}| = \max_{\lambda} \,\,|{\it \varphi}_{45,\hspace{0.05cm}i}(\lambda)| \hspace{0.05cm}.$$
- The special case $φ_\text{45, 45}(λ = 0)$ gives the PACF value of the spreading sequence with the octal identifier $(45)$.
In the course of this exercise and in the sample solution the following signals are mentioned:
- $q(t)$: binary bipolar source signal, symbol duration $T$,
- $c(t)$: $±1$ spreading signal, chip duration $T_c$,
- $s(t)$: band-spread transmission signal; it holds that $s(t) = q(t) · c(t)$, amplitude $±s_0$, chip duration $T_c$,
- $n(t)$: AWGN noise, characterized by the quotient $E_{\rm B}/N_0$,
- $i(t)$: interference signal of the interfering subscriber,
- $r(t)$: received signal; it holds that $r(t) = s(t) + n(t) + i(t)$,
- $b(t)$: band-compressed signal; it holds that $b(t)= r(t) · c(t)$,
- $d(t)$: detection signal after integration of $b(t)$ over the symbol duration $T$,
- $v(t)$: sink signal, comparison with $q(t)$ gives the error probability.
Notes:
- The exercise belongs to the chapter Error Probability of Direct-Sequence Spread Spectrum Modulation.
- Reference is made in particular to the section Two users with M-sequence spreading.
- For the so-called Q-function, the following approximations can be assumed:
- $$ {\rm Q} (2) \approx 0.02275, \hspace{0.2cm}{\rm Q} (3) \approx 0.00135, \hspace{0.2cm}{\rm Q} (5) \approx 2.45 \cdot 10^{-7} \hspace{0.05cm}.$$
Questions
Solution
- $$p_{\rm B} = {\rm Q}(2.515) = {\rm Q}({s_0}/{\sigma_d}) \hspace{0.3cm}\Rightarrow\hspace{0.3cm} \frac{\sigma_d}{s_0} = \frac{1}{2.515} = 0.398 \hspace{0.15cm}\underline {\approx 0.4} \hspace{0.05cm}.$$
- However, one could also calculate this quantity using the more general equation
- $$ \sigma_d^2 = \frac{N_0}{2 }\cdot\int^{+\infty}_{-\infty} |H_{\rm I}(f) |^2 \,\,{\rm d} {\it f}\hspace{0.05cm} = \frac{N_0}{2 }\cdot\int^{+\infty}_{-\infty}{\rm sinc}^2(f T)\,\,{\rm d} {\it f} = \frac{N_0}{2T } \hspace{0.05cm}.$$
- Here $H_{\rm I}(f)$ describes the integrator in the frequency domain.
- With $E_{\rm B}= s_0^2 · T$ the same result is obtained:
- $$\frac{\sigma_d^2}{s_0^2} = \frac{N_0}{2 \cdot s_0^2 \cdot T } = \frac{N_0}{2 E_{\rm B} } = \frac{0.316}{2 } = 0.158\hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\sigma_d}/{s_0} = 0.398 \approx 0.4 \hspace{0.05cm}.$$
(2) If the interfering participant uses the same M-sequence $(45)$ as the considered user,
then the (normalized) detection samples (without noise) are equal to $+2$ $($at $25\%)$, $-2$ $($at $25\%)$ and $0$ $($at $50\%)$.
- When $d(νT) = ±2$, the error probability for the considered user is significantly reduced.
- In this case, both users transmit the same bit $($"$+1$" or "$-1$"$)$ and the distance from the threshold is doubled:
- $$ p_{\rm B}\,\,\big [{\rm if}\,\, d (\nu T) = \pm 2s_0 \big ] = {\rm Q} \left ( 2 \cdot 2.515 \right ) = {\rm Q} \left ( 5.03 \right ) \approx 2.45 \cdot 10^{-7} \approx 0 \hspace{0.05cm}.$$
- On the other hand, if $d(νT) = 0$ (for example, if $a_\text{1(s)} = +1$ and $a_\text{1(i)} = -1$ holds or vice versa), the signals cancel completely and we obtain
- $$p_{\rm B}\big[{\rm if}\,\, d (\nu T) = 0 \big] = {\rm Q} \left ( 0 \right ) = 0.5 \hspace{0.05cm}.$$
- Averaging over these two equally probable possibilities, we thus obtain for the mean bit error probability:
- $$p_{\rm B}= 0.5 \cdot 2.45 \cdot 10^{-7}+ 0.5 \cdot 0.5 \hspace{0.15cm}\underline {\approx 25\%} \hspace{0.05cm}.$$
(3) We first consider only the useful part ⇒ $n(t) = 0$, restricting ourselves to the first data symbol and assuming the coefficient $a_\text{1(s)} = +1$.
- Then within this data bit $s(t) = c_{45}(t)$ holds.
- If the coefficient $a_\text{1(i)} $ of the interfering participant is also $+1$, then for the signals specified in front in the time interval from $0$ to $T$ we obtain:
- $$ r(t) = c_{45}(t) + c_{75}(t)\hspace{0.05cm},$$
- $$b(t) = r(t) \cdot c_{45}(t) = \left [c_{45}(t) + c_{75}(t) \right ] \cdot c_{45}(t) = 1+ c_{45}(t) \cdot c_{75}(t) \hspace{0.05cm},$$
- $$ d (T) = \frac{1}{T} \cdot \int_{0 }^{ T} b (t )\hspace{0.1cm} {\rm d}t = 1 + {\it \varphi}_{45,\hspace{0.05cm}75}(\lambda = 0) \hspace{0.05cm}.$$
- Here, $φ_\text{45, 75}(τ)$ denotes the PCCF between the spreading sequences with octal identifiers $(45)$ and $(75)$, which can be found in the table on the data page.
- Correspondingly, for the detection sample without noise, given $a_\text{1(s)} = +1$ and $a_\text{1(i)} =-1$:
- $$d (T) = 1 - {\it \varphi}_{45,\hspace{0.05cm}75}(\lambda = 0) \hspace{0.05cm}.$$
- For symmetry reasons, the coefficients $a_\text{1(s)} = -1$, $a_\text{1(i)} = -1$ as well as $a_\text{1(s)} = -1$, $a_\text{1(i)} = +1$ provide exactly the same contributions for the bit error probability as $a_\text{1(s)} = +1$, $a_\text{1(i)} = +1$ and $a_{1(s)} = +1$, $a_{1(i)} = -1$ respectively, if we also consider the AWGN noise.
- Thus, using the result of subtask (1) and with $φ_\text{45, 75}(λ = 0) = 7/31$, we obtain approximately:
- $$p_{\rm B} = \frac{1}{2} \cdot {\rm Q} \left ( \frac{1+ 7/31}{0.4} \right ) + \frac{1}{2} \cdot {\rm Q} \left ( \frac{1- 7/31}{0.4} \right ) = \frac{1}{2} \cdot {\rm Q} \left ( \frac{1.225}{0.4} \right ) + \frac{1}{2} \cdot {\rm Q} \left ( \frac{0.775}{0.4} \right ) = \frac{1}{2} \cdot {\rm Q} \left ( 3.06 \right ) + \frac{1}{2} \cdot {\rm Q} \left ( 1.94 \right )$$
- $$ \Rightarrow \hspace{0.3cm} p_{\rm B}\approx \frac{1}{2} \cdot \left [{\rm Q} \left ( 3 \right ) + {\rm Q} \left ( 2 \right ) \right ] = \frac{1}{2} \cdot \left [0.00135 + 0.02275 \right ] \hspace{0.15cm}\underline {= 1.2\%}\hspace{0.05cm}.$$
(4) Possible solutions are 2 and 3:
- The PCCF value $φ_\text{45, 57}(λ = 0)$ is only $1/31$ in magnitude and thus the error probability is only slightly larger than $0.6\%$.
- In contrast, the sequence with octal identifiers $(67)$ leads to the same PCCF as sequence $(75)$.
- Without interfering participants, the following applies according to the data sheet: $p_{\rm B} = 0.6\%$.
- With interference, this value cannot be undercut ⇒ solution 1 is not possible.