Difference between revisions of "Aufgaben:Exercise 3.6Z: Examination Correction"
| (4 intermediate revisions by 2 users not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID148__Sto_Z_3_6.png|right|frame| | + | [[File:P_ID148__Sto_Z_3_6.png|right|frame|Table for ${\rm \phi}(x)$ and ${\rm Q}(x)$]] |
| − | In an exam at the TU Munich $1000$ students participated. From the grade "4.0" upwards up to "1.0" the exam is considered to be passed. The exam regulations provide for the following grades: | + | In an exam at the TU Munich $1000$ students participated. From the grade "4.0" upwards up to "1.0" the exam is considered to be passed. The exam regulations provide for the following grades: |
:$$1.0, \ 1.3, \ 1.7, \ 2.0, \ 2.3, \ 2.7, \ 3.0, \ 3.3, \ 3.7, \ 4.0, \ 4.3, \ 4.7, \ 5.0.$$ | :$$1.0, \ 1.3, \ 1.7, \ 2.0, \ 2.3, \ 2.7, \ 3.0, \ 3.3, \ 3.7, \ 4.0, \ 4.3, \ 4.7, \ 5.0.$$ | ||
| − | Further, the exercise must take into account: | + | Further, the exercise must take into account: |
*The maximum achievable score is $100$. The best student achieved $88$ points. | *The maximum achievable score is $100$. The best student achieved $88$ points. | ||
| − | *Due to the relatively large number of participants, the achieved score – this is the random variable $z$ – with good approximation a [[Theory_of_Stochastic_Signals/Gaussian_Distributed_Random_Variables#Probability_density_function_.26_cumulative_density_function|Gaussian distribution]] with mean $m_z = 60$ and | + | *Due to the relatively large number of participants, the achieved score – this is the random variable $z$ – has with good approximation a [[Theory_of_Stochastic_Signals/Gaussian_Distributed_Random_Variables#Probability_density_function_.26_cumulative_density_function|Gaussian distribution]] with mean $m_z = 60$ and standard deviation $\sigma_z = 10$. |
| − | *In the correction, not only whole scores were assigned, but also (arbitrary) intermediate values, so that the random variable $z$ can be taken as "continuous" with good approximation. | + | *In the correction,&nbs |
| + | p; not only whole scores were assigned, but also (arbitrary) intermediate values, so that the random variable $z$ can be taken as "continuous valued" with good approximation. | ||
| − | For scoring, the guidelines given are: | + | For scoring, the guidelines given are: |
| − | *Even with six points less than the best $($so from $82$ points$)$ one shall get "1.0". | + | *Even with six points less than the best $($so from $82$ points$)$ one shall get "1.0". |
| − | *If one $46\%$ of the total score, one has passed the exam. | + | *If one reaches $46\%$ of the total score, one has passed the exam. |
*The points/grades assignment shall be linear. | *The points/grades assignment shall be linear. | ||
| Line 23: | Line 24: | ||
Hints: | Hints: | ||
| − | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Gaussian_Distributed_Random_Variables|Gaussian distributed random variables]]. | + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Gaussian_Distributed_Random_Variables|Gaussian distributed random variables]]. |
| − | + | *The "Gaussian distribution" is often called "normal distribution". This is not quite correct: | |
| − | * | + | *A normally distributed random variable $z$ does have a Gaussian PDF and CDF, but always with mean $m_z = 0$ and standard deviation $\sigma_z = 1$. |
| − | *A normally distributed random variable $z$ does have a Gaussian PDF and CDF, but always with mean $m_z = 0$ and | ||
| Line 32: | Line 32: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {What criteria should be considered in problem creation so that the grades will result in "approximately a normal distribution"? | + | {What criteria should be considered in problem creation so that the grades will result in "approximately a normal distribution"? |
|type="[]"} | |type="[]"} | ||
+ There are many exam participants. | + There are many exam participants. | ||
| Line 40: | Line 40: | ||
| − | {How many examinees are expected to score "1.0"? | + | {How many examinees are expected to score "1.0"? |
|type="{}"} | |type="{}"} | ||
$N_\text{1.0} \ = \ $ { 14 3% } | $N_\text{1.0} \ = \ $ { 14 3% } | ||
| − | {How many examinees are likely to fail the exam? Take into account that $z$ can be taken as a continuous random variable. | + | {How many examinees are likely to fail the exam? Take into account that $z$ can be taken as a continuous valued random variable. |
|type="{}"} | |type="{}"} | ||
$N_\text{4.3 ... 5.0} \ = \ $ { 81 3% } | $N_\text{4.3 ... 5.0} \ = \ $ { 81 3% } | ||
| − | {Specify the points/grades | + | {Specify the points/grades assignment. At what point do you get a "3.0"? How many examinees will get this grade? |
|type="{}"} | |type="{}"} | ||
$N_\text{3.0} \ = \ $ { 159 3% } | $N_\text{3.0} \ = \ $ { 159 3% } | ||
| − | {How many examinees are expected to receive the grade "2.7"? Justify why exactly that many examinees will receive the grade "3.3". | + | {How many examinees are expected to receive the grade "2.7"? Justify why exactly that many examinees will receive the grade "3.3". |
|type="{}"} | |type="{}"} | ||
$N_\text{2.7} \ = \ $ { 146 3% } | $N_\text{2.7} \ = \ $ { 146 3% } | ||
| Line 68: | Line 68: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Correct are <u>the solutions 1 and 3</u>: | + | '''(1)''' Correct are <u>the solutions 1 and 3</u>: |
| − | *According to the central limit theorem, a Gaussian distribution is obtained for the sum of many independent quantities. | + | *According to the central limit theorem, a Gaussian distribution is obtained for the sum of many independent quantities. |
| − | *Conversely, if there are only a few dependent tasks, there is no Gaussian distribution. | + | *Conversely, if there are only a few dependent tasks, there is no Gaussian distribution. |
| − | *A single yes/no question leads to a two-point distribution ($0$ points or maximum number of points). | + | *A single yes/no question leads to a two-point distribution ($0$ points or maximum number of points). |
| − | *Even if these imperatives are followed, a Gaussian distribution will not be expected for very few participants. | + | *Even if these imperatives are followed, a Gaussian distribution will not be expected for very few participants. |
| − | '''(2)''' One gets a "1.0" with $82$ points or more. | + | '''(2)''' One gets a "1.0" with $82$ points or more. |
| − | *Therefore, with the mean $m_z = 60$ and the | + | *Therefore, with the mean $m_z = 60$ and the standard deviation $\sigma_z = 10$: |
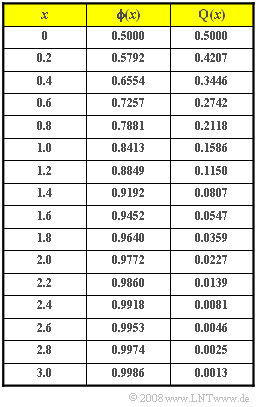
:$$\rm Pr(\it z\ge \rm 82)=\rm Q\Bigg(\frac{\rm 82-60}{\rm 10}\Bigg)=\rm Q(\rm 2.2) | :$$\rm Pr(\it z\ge \rm 82)=\rm Q\Bigg(\frac{\rm 82-60}{\rm 10}\Bigg)=\rm Q(\rm 2.2) | ||
\hspace{0.15cm}{=\rm 0.0139}.$$ | \hspace{0.15cm}{=\rm 0.0139}.$$ | ||
| − | *For a thousand participants, it follows $N_\text{1.0}\hspace{0.15cm}\underline{= 14}$. | + | *For a thousand participants, it follows $N_\text{1.0}\hspace{0.15cm}\underline{= 14}$. |
| Line 87: | Line 87: | ||
'''(3)''' With less than $46$ points, one has failed the exam: | '''(3)''' With less than $46$ points, one has failed the exam: | ||
:$$\rm Pr(\it z<\rm 46)=\rm Pr(\it z \le \rm 46)=\rm \phi\Bigg(\frac{\rm 46-60}{\rm 10}\Bigg)=\rm \phi(\rm -1.4)=\rm Q(\rm 1.4)=\rm 0.0807.$$ | :$$\rm Pr(\it z<\rm 46)=\rm Pr(\it z \le \rm 46)=\rm \phi\Bigg(\frac{\rm 46-60}{\rm 10}\Bigg)=\rm \phi(\rm -1.4)=\rm Q(\rm 1.4)=\rm 0.0807.$$ | ||
| − | *So <u>81 students have to compete again</u>. | + | *So <u>81 students have to compete again</u>. |
| − | '''(4)''' The difference in points $82 - 46 = 36$ must be divided among nine grade intervals $(1.3$, ... , $4.0)$ | + | '''(4)''' The difference in points $82 - 46 = 36$ must be divided among nine grade intervals $(1.3$, ... , $4.0)$. |
*Each interval thus comprises $4$ points. | *Each interval thus comprises $4$ points. | ||
| − | *For example, one receives a grade of "3.0" if one $58$ to $62$ points. | + | *For example, one receives a grade of "3.0" if one has $58$ to $62$ points. |
| − | *The probability that the grade is in this range is given by | + | *The probability that the grade is in this range is given by |
:$$\rm Pr(\rm 58 <\it z<\rm 62)=\rm \phi\Bigg(\frac{\rm 62-60}{\rm 10}\Bigg)-\rm \phi\Bigg(\frac{\rm 58-60}{\rm 10}\Bigg).$$ | :$$\rm Pr(\rm 58 <\it z<\rm 62)=\rm \phi\Bigg(\frac{\rm 62-60}{\rm 10}\Bigg)-\rm \phi\Bigg(\frac{\rm 58-60}{\rm 10}\Bigg).$$ | ||
| − | Taking advantage of the symmetry, one obtains: | + | *Taking advantage of the symmetry, one obtains: |
:$$\rm Pr(\rm 58 <\it z<\rm 62) = \rm \phi(\rm 0.2)-\rm \phi(\rm -0.2) = \rm 0.5792-\rm 0.4207=0.1587\hspace{0.2cm}\hspace{0.15cm}\underline{(159 \hspace{0.1cm}\rm participants)}.$$ | :$$\rm Pr(\rm 58 <\it z<\rm 62) = \rm \phi(\rm 0.2)-\rm \phi(\rm -0.2) = \rm 0.5792-\rm 0.4207=0.1587\hspace{0.2cm}\hspace{0.15cm}\underline{(159 \hspace{0.1cm}\rm participants)}.$$ | ||
| − | + | Notes: | |
| − | *$z$ is to be taken as a continuous random variable. Therefore, the score $62$ is simultaneously the upper bound for the "3.0"& | + | *$z$ is to be taken as a continuous valued random variable. |
| − | *If $z$ were only an integer, then $62$ would have to be assigned to either the "2.7" grade or the "3.0" grade, depending on the mood of the corrector. Of course, this would have to be done in the same way for all examinees. | + | *Therefore, the score $62$ is simultaneously the upper bound for the grade "3.0" as well as the lower bound for the grade "2.7." |
| + | *If $z$ were only an integer, then $62$ would have to be assigned to either the "2.7" grade or the "3.0" grade, depending on the mood of the corrector. | ||
| + | *Of course, this would have to be done in the same way for all examinees. | ||
| − | '''(5)''' Analogous to the | + | '''(5)''' Analogous to the solution of the subtask '''(4)''' applies to the grade "2.7": |
:$$\rm Pr(\rm 62 <\it z<\rm 66)=\rm \phi(\rm 0.6)-\rm \phi(\rm 0.2)=\rm 0.7257-\rm 0.5792=0.1465.$$ | :$$\rm Pr(\rm 62 <\it z<\rm 66)=\rm \phi(\rm 0.6)-\rm \phi(\rm 0.2)=\rm 0.7257-\rm 0.5792=0.1465.$$ | ||
| − | *For reasons of symmetry, the same value is obtained for the grade "3.3": | + | *For reasons of symmetry, the same value is obtained for the grade "3.3": |
:$$\rm Pr(\rm 54 <\it z<\rm 58)=\rm \phi(-\rm 0.2)-\rm \phi(-\rm 0.6)= \rm Q(\rm 0.2)-\rm Q(\rm 0.6)=\rm 0.1465.$$ | :$$\rm Pr(\rm 54 <\it z<\rm 58)=\rm \phi(-\rm 0.2)-\rm \phi(-\rm 0.6)= \rm Q(\rm 0.2)-\rm Q(\rm 0.6)=\rm 0.1465.$$ | ||
| − | *So <u>each 146 participants receive a grade of "2.7" or "3.3"</u>. | + | *So <u>each 146 participants receive a grade of "2.7" or "3.3"</u>. |
| − | '''(6)''' With the points | + | '''(6)''' With the points/grade assignment made here, not only the points are distributed around $m_z = 60$ symmetrically, but also the scores around "3.0". There are |
| − | *exactly as many "2.7"s as "3.3"s $($around $±0.3$ away from $3.0$ $)$, | + | *exactly as many "2.7"s as "3.3"s $($around $±0.3$ away from $3.0$ $)$, |
| − | *exactly as many "2.3 "s as "3.7"s $(3.0 ±0.7)$, and | + | *exactly as many "2.3 "s as "3.7"s $(3.0 ±0.7)$, and |
| − | *exactly as many "1.0 "s as "5.0 "s. | + | *exactly as many "1.0 "s as "5.0 "s. |
| − | Therefore, the $\rm mean\hspace{0.15cm} grade\hspace{0.15cm}\underline{ 3.0}$ results. | + | Therefore, the $\rm mean\hspace{0.15cm} grade\hspace{0.15cm}\underline{ 3.0}$ results. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 16:05, 17 February 2022
In an exam at the TU Munich $1000$ students participated. From the grade "4.0" upwards up to "1.0" the exam is considered to be passed. The exam regulations provide for the following grades:
- $$1.0, \ 1.3, \ 1.7, \ 2.0, \ 2.3, \ 2.7, \ 3.0, \ 3.3, \ 3.7, \ 4.0, \ 4.3, \ 4.7, \ 5.0.$$
Further, the exercise must take into account:
- The maximum achievable score is $100$. The best student achieved $88$ points.
- Due to the relatively large number of participants, the achieved score – this is the random variable $z$ – has with good approximation a Gaussian distribution with mean $m_z = 60$ and standard deviation $\sigma_z = 10$.
- In the correction,&nbs
p; not only whole scores were assigned, but also (arbitrary) intermediate values, so that the random variable $z$ can be taken as "continuous valued" with good approximation.
For scoring, the guidelines given are:
- Even with six points less than the best $($so from $82$ points$)$ one shall get "1.0".
- If one reaches $46\%$ of the total score, one has passed the exam.
- The points/grades assignment shall be linear.
Hints:
- The exercise belongs to the chapter Gaussian distributed random variables.
- The "Gaussian distribution" is often called "normal distribution". This is not quite correct:
- A normally distributed random variable $z$ does have a Gaussian PDF and CDF, but always with mean $m_z = 0$ and standard deviation $\sigma_z = 1$.
Questions
Solution
- According to the central limit theorem, a Gaussian distribution is obtained for the sum of many independent quantities.
- Conversely, if there are only a few dependent tasks, there is no Gaussian distribution.
- A single yes/no question leads to a two-point distribution ($0$ points or maximum number of points).
- Even if these imperatives are followed, a Gaussian distribution will not be expected for very few participants.
(2) One gets a "1.0" with $82$ points or more.
- Therefore, with the mean $m_z = 60$ and the standard deviation $\sigma_z = 10$:
- $$\rm Pr(\it z\ge \rm 82)=\rm Q\Bigg(\frac{\rm 82-60}{\rm 10}\Bigg)=\rm Q(\rm 2.2) \hspace{0.15cm}{=\rm 0.0139}.$$
- For a thousand participants, it follows $N_\text{1.0}\hspace{0.15cm}\underline{= 14}$.
(3) With less than $46$ points, one has failed the exam:
- $$\rm Pr(\it z<\rm 46)=\rm Pr(\it z \le \rm 46)=\rm \phi\Bigg(\frac{\rm 46-60}{\rm 10}\Bigg)=\rm \phi(\rm -1.4)=\rm Q(\rm 1.4)=\rm 0.0807.$$
- So 81 students have to compete again.
(4) The difference in points $82 - 46 = 36$ must be divided among nine grade intervals $(1.3$, ... , $4.0)$.
- Each interval thus comprises $4$ points.
- For example, one receives a grade of "3.0" if one has $58$ to $62$ points.
- The probability that the grade is in this range is given by
- $$\rm Pr(\rm 58 <\it z<\rm 62)=\rm \phi\Bigg(\frac{\rm 62-60}{\rm 10}\Bigg)-\rm \phi\Bigg(\frac{\rm 58-60}{\rm 10}\Bigg).$$
- Taking advantage of the symmetry, one obtains:
- $$\rm Pr(\rm 58 <\it z<\rm 62) = \rm \phi(\rm 0.2)-\rm \phi(\rm -0.2) = \rm 0.5792-\rm 0.4207=0.1587\hspace{0.2cm}\hspace{0.15cm}\underline{(159 \hspace{0.1cm}\rm participants)}.$$
Notes:
- $z$ is to be taken as a continuous valued random variable.
- Therefore, the score $62$ is simultaneously the upper bound for the grade "3.0" as well as the lower bound for the grade "2.7."
- If $z$ were only an integer, then $62$ would have to be assigned to either the "2.7" grade or the "3.0" grade, depending on the mood of the corrector.
- Of course, this would have to be done in the same way for all examinees.
(5) Analogous to the solution of the subtask (4) applies to the grade "2.7":
- $$\rm Pr(\rm 62 <\it z<\rm 66)=\rm \phi(\rm 0.6)-\rm \phi(\rm 0.2)=\rm 0.7257-\rm 0.5792=0.1465.$$
- For reasons of symmetry, the same value is obtained for the grade "3.3":
- $$\rm Pr(\rm 54 <\it z<\rm 58)=\rm \phi(-\rm 0.2)-\rm \phi(-\rm 0.6)= \rm Q(\rm 0.2)-\rm Q(\rm 0.6)=\rm 0.1465.$$
- So each 146 participants receive a grade of "2.7" or "3.3".
(6) With the points/grade assignment made here, not only the points are distributed around $m_z = 60$ symmetrically, but also the scores around "3.0". There are
- exactly as many "2.7"s as "3.3"s $($around $±0.3$ away from $3.0$ $)$,
- exactly as many "2.3 "s as "3.7"s $(3.0 ±0.7)$, and
- exactly as many "1.0 "s as "5.0 "s.
Therefore, the $\rm mean\hspace{0.15cm} grade\hspace{0.15cm}\underline{ 3.0}$ results.