Difference between revisions of "Aufgaben:Exercise 3.9: Characteristic Curve for Cosine PDF"
From LNTwww
| (3 intermediate revisions by 2 users not shown) | |||
| Line 4: | Line 4: | ||
[[File:P_ID136__Sto_A_3_9.png|right|frame|Rectangular and cosine PDF]] | [[File:P_ID136__Sto_A_3_9.png|right|frame|Rectangular and cosine PDF]] | ||
| − | We are looking for a continuous, monotonically increasing nonlinear characteristic $y =g(x)$, which generates a new random variable with "cosine" PDF from a between $-1$ and $+1$ uniformly distributed random variable $x$ | + | We are looking for a continuous, monotonically increasing nonlinear characteristic $y =g(x)$, which generates a new random variable with "cosine" PDF from a between $-1$ and $+1$ uniformly distributed random variable $x$: |
:$$f_y(y)=A\cdot\cos({\pi}/{2}\cdot y).$$ | :$$f_y(y)=A\cdot\cos({\pi}/{2}\cdot y).$$ | ||
| − | *The random variable $y$ can also only take values between $-1$ and $+1$ | + | *The random variable $y$ can also only take values between $-1$ and $+1$. |
| − | *The two density functions $f_x(x)$ and $f_y(y)$ are sketched | + | *The two density functions $f_x(x)$ and $f_y(y)$ are sketched on the right. |
| − | |||
| − | |||
| − | |||
| Line 17: | Line 14: | ||
Hints: | Hints: | ||
| − | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Exponentially_Distributed_Random_Variables | + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Exponentially_Distributed_Random_Variables|Exponentially Distributed Random Variables]]. |
*In particular, reference is made to the page [[Theory_of_Stochastic_Signals/Exponentially_Distributed_Random_Variables#Transformation_of_random_variables|Transformation of random variables]]. | *In particular, reference is made to the page [[Theory_of_Stochastic_Signals/Exponentially_Distributed_Random_Variables#Transformation_of_random_variables|Transformation of random variables]]. | ||
| Line 28: | Line 25: | ||
{Which of the following statements are true? | {Which of the following statements are true? | ||
|type="[]"} | |type="[]"} | ||
| − | + Outside the range $-1 \le x \le +1$ | + | + Outside the range $-1 \le x \le +1$ ⇒ $g(x)$ can be arbitrary. |
- The characteristic curve must be symmetrical about $x= 0$ : $g(-x) = g(x)$. | - The characteristic curve must be symmetrical about $x= 0$ : $g(-x) = g(x)$. | ||
+ The random variable $y$ has a smaller variance than $x$. | + The random variable $y$ has a smaller variance than $x$. | ||
| − | {Calculate the $f_y(y)$ | + | {Calculate the $f_y(y)$ value at $y = 0$: $A = f_y(0)$. |
|type="{}"} | |type="{}"} | ||
$A \ = \ $ { 0.785 3% } | $A \ = \ $ { 0.785 3% } | ||
| − | {Determine the slope $h\hspace{0.05cm}'(y)$ of the inverse function $x = h(y)$, where for $|y| \le 1$ always $h\hspace{0.05cm}'(y) > 0$ should hold? What slope holds for $y = 0$ ? | + | {Determine the slope $h\hspace{0.05cm}'(y)$ of the inverse function $x = h(y)$, where for $|y| \le 1$ always $h\hspace{0.05cm}'(y) > 0$ should hold? What slope holds for $y = 0$ ? |
|type="{}"} | |type="{}"} | ||
$h'(y = 0) \ = \ $ { 1.571 3% } | $h'(y = 0) \ = \ $ { 1.571 3% } | ||
| Line 48: | Line 45: | ||
| − | {Determine the function | + | {Determine the function $y = g(x)$ of the characteristic we are looking for. What is the function value at the point $x = 1$ ? |
|type="{}"} | |type="{}"} | ||
$g(x = 1) \ = \ $ { 1 3% } | $g(x = 1) \ = \ $ { 1 3% } | ||
| Line 59: | Line 56: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Correct are <u>statements 1 and 3</u>: | + | '''(1)''' Correct are the <u>statements 1 and 3</u>: |
| − | *Since $x$ can only take values between $\pm 1$ | + | *Since $x$ can only take values between $\pm 1$, the course of the characteristic curve outside of this range is irrelevant for the random variable $y$. |
*The condition $g(-x) = g(x)$ does not have to be met. There are any number of characteristic curves that can generate the desired PDF. | *The condition $g(-x) = g(x)$ does not have to be met. There are any number of characteristic curves that can generate the desired PDF. | ||
| − | *For example, the characteristic curve calculated in point '''(5)''' is point symmetric: $g(-x) = -g(x)$. | + | *For example, the characteristic curve calculated in point '''(5)''' is point-symmetric: $g(-x) = -g(x)$. |
| − | *The graphical representations of the two density functions already show that $\sigma_y^2 < \sigma_x^2$ | + | *The graphical representations of the two density functions already show that $\sigma_y^2 < \sigma_x^2$. |
| Line 72: | Line 69: | ||
| − | '''(3)''' The transformation formula can be | + | '''(3)''' The transformation formula can be described as follows: |
:$$f_y(y)=\frac{f_x(x)}{| g'(x)|}\Big|_{\, x=h(y)}=f_x(x)\cdot |h'(y)| \Big|_{\, x=h(y)}.$$ | :$$f_y(y)=\frac{f_x(x)}{| g'(x)|}\Big|_{\, x=h(y)}=f_x(x)\cdot |h'(y)| \Big|_{\, x=h(y)}.$$ | ||
*The inverse function $x = h(y)$ of a monotonically increasing characteristic $y = g(x)$ also increases monotonically. | *The inverse function $x = h(y)$ of a monotonically increasing characteristic $y = g(x)$ also increases monotonically. | ||
| − | *Therefore the | + | *Therefore one does not need to make use of the absolute value and subsequently obtains: |
:$$h\hspace{0.05cm}'(y)=\frac{f_y(y)}{f_x(x)\Big|_{\, x=h(y)}}={\pi}/{\rm 2}\cdot \cos({\pi}/{2}\cdot y).$$ | :$$h\hspace{0.05cm}'(y)=\frac{f_y(y)}{f_x(x)\Big|_{\, x=h(y)}}={\pi}/{\rm 2}\cdot \cos({\pi}/{2}\cdot y).$$ | ||
| Line 89: | Line 86: | ||
:$$h(y) = \sin({\pi}/{2}\cdot y) \hspace{0.5cm} \rightarrow\hspace{0.5cm} | :$$h(y) = \sin({\pi}/{2}\cdot y) \hspace{0.5cm} \rightarrow\hspace{0.5cm} | ||
h(y = 1) \hspace{0.15cm}\underline{= +1}.$$ | h(y = 1) \hspace{0.15cm}\underline{= +1}.$$ | ||
| − | |||
| Line 95: | Line 91: | ||
:$$y=g(x)={\rm 2}/{\rm \pi}\cdot \rm arcsin({\it x}).$$ | :$$y=g(x)={\rm 2}/{\rm \pi}\cdot \rm arcsin({\it x}).$$ | ||
| − | *This characteristic increases monotonically in the range $-1 \le x \le +1$ from $y = -1$ to $y = +1$ . | + | *This characteristic curve increases monotonically in the range $-1 \le x \le +1$ from $y = -1$ to $y = +1$ . |
*So the value we are looking for is $g(x= 1) \hspace{0.15cm}\underline{= +1}$. | *So the value we are looking for is $g(x= 1) \hspace{0.15cm}\underline{= +1}$. | ||
Latest revision as of 15:27, 2 February 2022
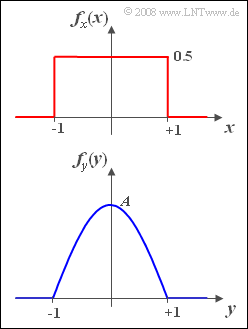
We are looking for a continuous, monotonically increasing nonlinear characteristic $y =g(x)$, which generates a new random variable with "cosine" PDF from a between $-1$ and $+1$ uniformly distributed random variable $x$:
- $$f_y(y)=A\cdot\cos({\pi}/{2}\cdot y).$$
- The random variable $y$ can also only take values between $-1$ and $+1$.
- The two density functions $f_x(x)$ and $f_y(y)$ are sketched on the right.
Hints:
- The exercise belongs to the chapter Exponentially Distributed Random Variables.
- In particular, reference is made to the page Transformation of random variables.
Question
Solution
(1) Correct are the statements 1 and 3:
- Since $x$ can only take values between $\pm 1$, the course of the characteristic curve outside of this range is irrelevant for the random variable $y$.
- The condition $g(-x) = g(x)$ does not have to be met. There are any number of characteristic curves that can generate the desired PDF.
- For example, the characteristic curve calculated in point (5) is point-symmetric: $g(-x) = -g(x)$.
- The graphical representations of the two density functions already show that $\sigma_y^2 < \sigma_x^2$.
(2) The integral over the PDF must always equal $1$ . It follows that:
- $$\int_{-\rm 1}^{\rm 1}A\cdot \cos({\pi}/{\rm 2}\cdot y)\, {\rm d} y=\frac{A\cdot \rm 4}{\pi}\hspace{0.3cm} \rightarrow\hspace{0.3cm} A=\frac{\pi}{\rm 4} \hspace{0.15cm}\underline{= \rm 0.785}.$$
(3) The transformation formula can be described as follows:
- $$f_y(y)=\frac{f_x(x)}{| g'(x)|}\Big|_{\, x=h(y)}=f_x(x)\cdot |h'(y)| \Big|_{\, x=h(y)}.$$
- The inverse function $x = h(y)$ of a monotonically increasing characteristic $y = g(x)$ also increases monotonically.
- Therefore one does not need to make use of the absolute value and subsequently obtains:
- $$h\hspace{0.05cm}'(y)=\frac{f_y(y)}{f_x(x)\Big|_{\, x=h(y)}}={\pi}/{\rm 2}\cdot \cos({\pi}/{2}\cdot y).$$
- At the point $y = 0$ the slope has the value $h\hspace{0.05cm}'(y= 0)=π/2\hspace{0.15cm}\underline{\approx 1.571}$.
(4) One obtains by (indefinite) integration:
- $$h(y)=\int h\hspace{0.05cm}'(y)\, {\rm d} y + C = \frac{\pi}{2}\cdot \frac{2}{\pi}\cdot \sin(\frac{\pi}{ 2}\cdot y) + C.$$
- The constraint $h(y= 0) = 0$ leads to the constant $C = 0$ and thus to the result:
- $$h(y) = \sin({\pi}/{2}\cdot y) \hspace{0.5cm} \rightarrow\hspace{0.5cm} h(y = 1) \hspace{0.15cm}\underline{= +1}.$$
(5) The inverse function of the function determined in subtask (4) is $x = h(y)$ :
- $$y=g(x)={\rm 2}/{\rm \pi}\cdot \rm arcsin({\it x}).$$
- This characteristic curve increases monotonically in the range $-1 \le x \le +1$ from $y = -1$ to $y = +1$ .
- So the value we are looking for is $g(x= 1) \hspace{0.15cm}\underline{= +1}$.