Difference between revisions of "Aufgaben:Exercise 3.9Z: Sine Transformation"
| (8 intermediate revisions by 3 users not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID137__Sto_Z_3_9.png|right|frame|Input PDF | + | [[File:P_ID137__Sto_Z_3_9.png|right|frame|Input PDF, characteristic curve]] |
| − | In this task, we consider a random variable $x$ with $\ | + | In this task, we consider a random variable $x$ with sine-square shaped $\rm PDF$ in the range between $x= 0$ and $x= 2$: |
| − | :$$f_x(x)= \sin^2({\rm\pi}/{\rm 2}\cdot x) \hspace{1cm}\rm for\hspace{0. | + | :$$f_x(x)= \sin^2({\rm\pi}/{\rm 2}\cdot x) \hspace{1cm}\rm for\hspace{0.25cm}{\rm 0\le \it x \le \rm 2} .$$ |
| − | Outside of this, the PDF is identically zero. | + | Outside of this, the PDF is identically zero. |
| − | The mean and | + | The mean and the standard deviation of this random variable $x$ have already been determined in the [[Aufgaben:Exercise_3.3:_Moments_for_cos²-PDF|Exercise 3.3]]: |
:$$m_x = 1,\hspace{0.2cm}\sigma_x = 0.361.$$ | :$$m_x = 1,\hspace{0.2cm}\sigma_x = 0.361.$$ | ||
| Line 15: | Line 15: | ||
:$$y= g(x) =\sin({\rm\pi}/{\rm 2}\cdot x).$$ | :$$y= g(x) =\sin({\rm\pi}/{\rm 2}\cdot x).$$ | ||
| − | The figure shows in each case in the range $0 \le x \le 2$: | + | The figure shows in each case in the range $0 \le x \le 2$: |
*above the PDF $f_x(x)$, | *above the PDF $f_x(x)$, | ||
*below the nonlinear characteristic $y = g(x)$. | *below the nonlinear characteristic $y = g(x)$. | ||
| Line 28: | Line 28: | ||
Hints: | Hints: | ||
*The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Exponentially_Distributed_Random_Variables|Exponentially Distributed Random Variables]]. | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Exponentially_Distributed_Random_Variables|Exponentially Distributed Random Variables]]. | ||
| − | *In particular, reference is made to the | + | *In particular, reference is made to the section [[Theory_of_Stochastic_Signals/Exponentially_Distributed_Random_Variables#Transformation_of_random_variables|"Transformation of random variables"]] and the chapter [[Theory_of_Stochastic_Signals/Expected_Values_and_Moments|"Expected Values and Moments"]]. |
*Given are the two indefinite integrals: | *Given are the two indefinite integrals: | ||
| Line 40: | Line 40: | ||
{Which of the following statements are true? | {Which of the following statements are true? | ||
|type="[]"} | |type="[]"} | ||
| − | - $y$ is limited to the | + | - $y$ is limited to the range $0 \le y \le 1$ . |
| − | + $y$ is limited to the | + | + $y$ is limited to the range $0 < y \le 1$ . |
+ The mean $m_y$ is less than the mean $m_x$. | + The mean $m_y$ is less than the mean $m_x$. | ||
| Line 50: | Line 50: | ||
| − | {Calculate the | + | {Calculate the the standard deviation of the random variable $y$. |
|type="{}"} | |type="{}"} | ||
$\sigma_y \ = \ $ { 0.172 3% } | $\sigma_y \ = \ $ { 0.172 3% } | ||
| − | {Calculate the PDF $f_y(y)$. Note the symmetry properties. What PDF | + | {Calculate the PDF $f_y(y)$. Note the symmetry properties. What PDF value results for $y = 0.6$? |
|type="{}"} | |type="{}"} | ||
$f_y(y=0.6) \ = \ $ { 0.573 3% } | $f_y(y=0.6) \ = \ $ { 0.573 3% } | ||
| − | {What is the PDF value for $y = 1$? Interpret the result. What is the probability that $y$ is exactly equal $1$ | + | {What is the PDF value for $y = 1$? Interpret the result. What is the probability that $y$ is exactly equal $1$? |
|type="{}"} | |type="{}"} | ||
${\rm Pr}(y=1) \ = \ $ { 0. } | ${\rm Pr}(y=1) \ = \ $ { 0. } | ||
| Line 69: | Line 69: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Correct are <u>the second and the third suggested solutions</u>: | + | '''(1)''' Correct are <u>the second and the third suggested solutions</u>: |
*Because of the range of values of $x$ and the given characteristic curve, $y$ cannot take values smaller than $0$ or larger than $1$ respectively. | *Because of the range of values of $x$ and the given characteristic curve, $y$ cannot take values smaller than $0$ or larger than $1$ respectively. | ||
| − | *The value $y = 0$ cannot occur either, however, since neither $x = 0$ nor $x = 2$ are possible. | + | *The value $y = 0$ cannot occur either, however, since neither $x = 0$ nor $x = 2$ are possible. |
| − | *With these properties, the result is surely $m_y < 1$, i.e., a smaller value than $m_x = 1$ (see specification). | + | *With these properties, the result is surely $m_y < 1$, i.e., a smaller value than $m_x = 1$ (see specification). |
| − | '''(2)''' To solve this task, one could, for example, first determine the PDF $f_y(y)$ and calculate $m_y$ from it in the usual way. | + | '''(2)''' To solve this task, one could, for example, first determine the PDF $f_y(y)$ and calculate $m_y$ from it in the usual way. |
*The direct way leads to the same result: | *The direct way leads to the same result: | ||
:$$m_y={\rm E}\big[y\big]={\rm E}\big[g(x)\big]=\int_{-\infty}^{+\infty}g(x)\cdot f_x(x)\,{\rm d}x.$$ | :$$m_y={\rm E}\big[y\big]={\rm E}\big[g(x)\big]=\int_{-\infty}^{+\infty}g(x)\cdot f_x(x)\,{\rm d}x.$$ | ||
| Line 89: | Line 89: | ||
*This leads to the result: | *This leads to the result: | ||
| − | :$$ m_{ 2 y}=\int_{\rm 0}^{\rm 2}\hspace{-0. 15cm}\sin^{\rm 4}({\rm \pi}/{\rm 2}\cdot x)\, {\rm d} x= \frac{\rm 3}{\rm 8}\cdot x-\frac{\rm 1}{\rm 2\cdot\pi}\cdot \sin(\rm \pi\cdot{\it x})+\frac{\rm 1}{\rm 16\cdot\pi}\cdot \sin(\rm 2 \pi\cdot {\it x})\Big|_{\rm 0}^{\rm 2} \hspace{0.15cm}{= \rm | + | :$$ m_{ 2 y}=\int_{\rm 0}^{\rm 2}\hspace{-0.15cm}\sin^{\rm 4}({\rm \pi}/{\rm 2}\cdot x)\,{\rm d} x= \frac{\rm 3}{\rm 8}\cdot x-\frac{\rm 1}{\rm 2\cdot\pi}\cdot \sin(\rm \pi\cdot{\it x})+\frac{\rm 1}{\rm 16\cdot\pi}\cdot \sin(\rm 2 \pi\cdot {\it x})\Big|_{\rm 0}^{\rm 2} \hspace{0.15cm}{= \rm |
0.75}.$$ | 0.75}.$$ | ||
| − | *With the result from '''(2)''' it thus follows for the | + | *With the result from '''(2)''' it thus follows for the standard deviation: |
:$$ \sigma_{y}=\sqrt{\frac{\rm 3}{\rm 4}-\Big(\frac{\rm 8}{\rm 3\cdot\pi}\Big)^{\rm 2}} \hspace{0.15cm}\underline{\approx \rm 0.172}.$$ | :$$ \sigma_{y}=\sqrt{\frac{\rm 3}{\rm 4}-\Big(\frac{\rm 8}{\rm 3\cdot\pi}\Big)^{\rm 2}} \hspace{0.15cm}\underline{\approx \rm 0.172}.$$ | ||
| − | '''(4)''' Due to the symmetry of PDF $f_x(x)$ and characteristic curve $y =g(x)$ um $x = 1$ the two domains yield. | + | '''(4)''' Due to the symmetry of the PDF $f_x(x)$ and the characteristic curve $y =g(x)$ um $x = 1$ the two domains yield. |
*$0 \le x \le 1$ and | *$0 \le x \le 1$ and | ||
*$1 \le x \le 2$ | *$1 \le x \le 2$ | ||
| Line 103: | Line 103: | ||
each give the same contribution for $f_y(y)$. | each give the same contribution for $f_y(y)$. | ||
| − | *In the first domain, the derivative of the characteristic curve is positive: $g\hspace{0.05cm}'(x)={\rm \pi}/{\rm 2}\cdot \cos({\rm \pi}/{\rm 2}\cdot x).$ | + | *In the first domain, the derivative of the characteristic curve is positive: $g\hspace{0.05cm}'(x)={\rm \pi}/{\rm 2}\cdot \cos({\rm \pi}/{\rm 2}\cdot x).$ |
*The inverse function is: $ x=h(y)={\rm 2}/{\rm \pi}\cdot \arcsin( y).$ | *The inverse function is: $ x=h(y)={\rm 2}/{\rm \pi}\cdot \arcsin( y).$ | ||
| − | *Taking into account the second contribution by the factor $2$ we get | + | *Taking into account the second contribution by the factor $2$ we get the searched PDF in the range $0 \le y \le 1$: |
:$$f_y(y)= 2\cdot\frac{\sin^{ 2}({ \pi}/{ 2}\cdot x)}{{ \pi}/{ 2}\cdot \cos({ \pi}/{ 2}\cdot x)}\Big|_{\, x={ 2}/{ \pi}\cdot \arcsin( y)}.$$ | :$$f_y(y)= 2\cdot\frac{\sin^{ 2}({ \pi}/{ 2}\cdot x)}{{ \pi}/{ 2}\cdot \cos({ \pi}/{ 2}\cdot x)}\Big|_{\, x={ 2}/{ \pi}\cdot \arcsin( y)}.$$ | ||
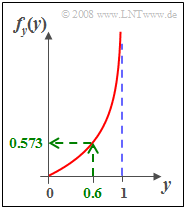
| − | [[File: | + | [[File:P_ID138__Sto_Z_3_9_e_neu.png|right|frame|PDF after transformation]] |
| − | * | + | *Outside of this range: $f_y(y) \equiv 0$. This leads to the intermediate result |
:$$f_y(y)=\frac{4}{\pi}\cdot \frac{\sin^{2}(\arcsin( y ))}{\sqrt{\rm 1-\sin^{ 2}(\arcsin( y \rm ))}}.$$ | :$$f_y(y)=\frac{4}{\pi}\cdot \frac{\sin^{2}(\arcsin( y ))}{\sqrt{\rm 1-\sin^{ 2}(\arcsin( y \rm ))}}.$$ | ||
| − | |||
*And because of $\sin\big (\arcsin(y)\big) = y$: | *And because of $\sin\big (\arcsin(y)\big) = y$: | ||
| − | :$$f_y(y)=\frac{ 4}{\pi}\cdot \frac{ y^{2}}{\sqrt{1- y^{\rm 2}}.$$ | + | :$$f_y(y)=\frac{ 4}{\pi}\cdot \frac{ y^{2}}{\sqrt{1- y^{\rm 2}}}.$$ |
*At the point $y = 0.6$ one obtains the value $f_y(y= 0.6)\hspace{0.15cm}\underline{=0.573}$. | *At the point $y = 0.6$ one obtains the value $f_y(y= 0.6)\hspace{0.15cm}\underline{=0.573}$. | ||
| − | *On the right, this PDF $f_y(y)$ is shown graphically. | + | *On the right, this PDF $f_y(y)$ is shown graphically. |
| − | '''(5)''' The PDF is infinitely large at the point $y = 1$ | + | '''(5)''' The PDF is infinitely large at the point $y = 1$. |
*This is due to the fact that at this point the derivative $g\hspace{0.05cm}'(x)$ of the characteristic curve runs horizontally. | *This is due to the fact that at this point the derivative $g\hspace{0.05cm}'(x)$ of the characteristic curve runs horizontally. | ||
| − | * However, since $y$ is a continuous random | + | * However, since $y$ is a continuous random quantity, nevertheless ${\rm Pr}(y = 1) \hspace{0.15cm}\underline{= 0}$ holds. |
This means: | This means: | ||
| − | *An infinity point in the PDF is not identical to a Dirac function. | + | *An infinity point in the PDF is not identical to a Dirac delta function. |
| − | *Or more casually expressed: An infinity point in the PDF is "less" than a Dirac function. | + | *Or more casually expressed: An infinity point in the PDF is "less" than a Dirac delta function. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 16:09, 17 February 2022
In this task, we consider a random variable $x$ with sine-square shaped $\rm PDF$ in the range between $x= 0$ and $x= 2$:
- $$f_x(x)= \sin^2({\rm\pi}/{\rm 2}\cdot x) \hspace{1cm}\rm for\hspace{0.25cm}{\rm 0\le \it x \le \rm 2} .$$
Outside of this, the PDF is identically zero.
The mean and the standard deviation of this random variable $x$ have already been determined in the Exercise 3.3:
- $$m_x = 1,\hspace{0.2cm}\sigma_x = 0.361.$$
Another random variable is obtained by transformation using the nonlinear characteristic curve
- $$y= g(x) =\sin({\rm\pi}/{\rm 2}\cdot x).$$
The figure shows in each case in the range $0 \le x \le 2$:
- above the PDF $f_x(x)$,
- below the nonlinear characteristic $y = g(x)$.
Hints:
- The exercise belongs to the chapter Exponentially Distributed Random Variables.
- In particular, reference is made to the section "Transformation of random variables" and the chapter "Expected Values and Moments".
- Given are the two indefinite integrals:
- $$\int \sin^{\rm 3}( ax)\,{\rm d}x = \frac{\rm 1}{ 3 a} \cdot \cos^{\rm 3}( ax)-\frac{\rm 1}{ a}\cdot \cos(ax),$$
- $$\int \sin^{\rm 4}(ax)\,{\rm d}x =\frac{\rm 3}{\rm 8}\cdot x-\frac{\rm 1}{\rm 4 a} \cdot \sin(2 ax)+\frac{\rm 1}{32 a}\cdot \sin(4 ax).$$
Questions
Solution
- Because of the range of values of $x$ and the given characteristic curve, $y$ cannot take values smaller than $0$ or larger than $1$ respectively.
- The value $y = 0$ cannot occur either, however, since neither $x = 0$ nor $x = 2$ are possible.
- With these properties, the result is surely $m_y < 1$, i.e., a smaller value than $m_x = 1$ (see specification).
(2) To solve this task, one could, for example, first determine the PDF $f_y(y)$ and calculate $m_y$ from it in the usual way.
- The direct way leads to the same result:
- $$m_y={\rm E}\big[y\big]={\rm E}\big[g(x)\big]=\int_{-\infty}^{+\infty}g(x)\cdot f_x(x)\,{\rm d}x.$$
- With the current functions $g(x)$ and $f_x(x)$ we obtain:
- $$m_y=\int_{\rm 0}^{\rm 2}\hspace{-0.1cm}\sin^{\rm 3}({\pi}/{ 2}\cdot x)\,{\rm d}x=\frac{\rm 2}{\rm 3\cdot \pi}\cdot \cos^{\rm 3}({\pi}/{ 2}\cdot x)-\frac{\rm 2}{\rm \pi} \cdot \cos({3 \rm \pi}/{\rm 2}\cdot x)\Big|_{\rm 0}^{\rm 2}=\frac{\rm 8}{\rm 3\cdot \pi} \hspace{0.15cm}\underline{=\rm 0.849}.$$
(3) By analogy with point (2) holds:
- $$m_{2 y}={\rm E}[y^{\rm 2}]={\rm E}[g^{\rm 2}( x)]=\int_{-\infty}^{+\infty}\hspace{-0.35cm}g^{2}( x)\cdot f_x(x)\,{\rm d}x.$$
- This leads to the result:
- $$ m_{ 2 y}=\int_{\rm 0}^{\rm 2}\hspace{-0.15cm}\sin^{\rm 4}({\rm \pi}/{\rm 2}\cdot x)\,{\rm d} x= \frac{\rm 3}{\rm 8}\cdot x-\frac{\rm 1}{\rm 2\cdot\pi}\cdot \sin(\rm \pi\cdot{\it x})+\frac{\rm 1}{\rm 16\cdot\pi}\cdot \sin(\rm 2 \pi\cdot {\it x})\Big|_{\rm 0}^{\rm 2} \hspace{0.15cm}{= \rm 0.75}.$$
- With the result from (2) it thus follows for the standard deviation:
- $$ \sigma_{y}=\sqrt{\frac{\rm 3}{\rm 4}-\Big(\frac{\rm 8}{\rm 3\cdot\pi}\Big)^{\rm 2}} \hspace{0.15cm}\underline{\approx \rm 0.172}.$$
(4) Due to the symmetry of the PDF $f_x(x)$ and the characteristic curve $y =g(x)$ um $x = 1$ the two domains yield.
- $0 \le x \le 1$ and
- $1 \le x \le 2$
each give the same contribution for $f_y(y)$.
- In the first domain, the derivative of the characteristic curve is positive: $g\hspace{0.05cm}'(x)={\rm \pi}/{\rm 2}\cdot \cos({\rm \pi}/{\rm 2}\cdot x).$
- The inverse function is: $ x=h(y)={\rm 2}/{\rm \pi}\cdot \arcsin( y).$
- Taking into account the second contribution by the factor $2$ we get the searched PDF in the range $0 \le y \le 1$:
- $$f_y(y)= 2\cdot\frac{\sin^{ 2}({ \pi}/{ 2}\cdot x)}{{ \pi}/{ 2}\cdot \cos({ \pi}/{ 2}\cdot x)}\Big|_{\, x={ 2}/{ \pi}\cdot \arcsin( y)}.$$
- Outside of this range: $f_y(y) \equiv 0$. This leads to the intermediate result
- $$f_y(y)=\frac{4}{\pi}\cdot \frac{\sin^{2}(\arcsin( y ))}{\sqrt{\rm 1-\sin^{ 2}(\arcsin( y \rm ))}}.$$
- And because of $\sin\big (\arcsin(y)\big) = y$:
- $$f_y(y)=\frac{ 4}{\pi}\cdot \frac{ y^{2}}{\sqrt{1- y^{\rm 2}}}.$$
- At the point $y = 0.6$ one obtains the value $f_y(y= 0.6)\hspace{0.15cm}\underline{=0.573}$.
- On the right, this PDF $f_y(y)$ is shown graphically.
(5) The PDF is infinitely large at the point $y = 1$.
- This is due to the fact that at this point the derivative $g\hspace{0.05cm}'(x)$ of the characteristic curve runs horizontally.
- However, since $y$ is a continuous random quantity, nevertheless ${\rm Pr}(y = 1) \hspace{0.15cm}\underline{= 0}$ holds.
This means:
- An infinity point in the PDF is not identical to a Dirac delta function.
- Or more casually expressed: An infinity point in the PDF is "less" than a Dirac delta function.