Difference between revisions of "Aufgaben:Exercise 4.3: Algebraic and Modulo Sum"
From LNTwww
| (5 intermediate revisions by one other user not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
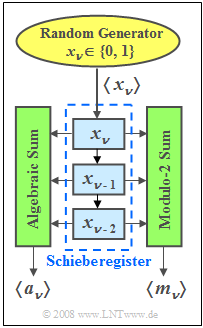
| − | [[File: | + | [[File:EN_Sto_A_4_3_neu2.png|right|frame|Algebraic & modulo–2 sum]] |
| − | A "clocked" random number generator returns a sequence $\langle x_\nu \rangle$ of binary random numbers. | + | |
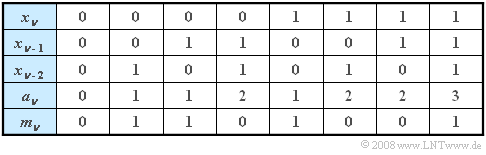
| + | [[File:P_ID254__Sto_A_4_3Tab.png|right|frame|Table for moment calculation]] | ||
| + | A "clocked" random number generator returns a sequence $\langle x_\nu \rangle$ of binary random numbers. | ||
*It is assumed that the binary numbers $0$ and $1$ occur with equal probabilities and that the individual random numbers do not depend on each other. | *It is assumed that the binary numbers $0$ and $1$ occur with equal probabilities and that the individual random numbers do not depend on each other. | ||
*The random numbers $ x_\nu \in \{0, 1\}$ are entered into the first memory location of a shift register and shifted down one digit with each clock pulse. | *The random numbers $ x_\nu \in \{0, 1\}$ are entered into the first memory location of a shift register and shifted down one digit with each clock pulse. | ||
| Line 11: | Line 13: | ||
Two new random sequences $\langle a_\nu \rangle$ and $\langle m_\nu \rangle$ are formed from the contents of the three-digit shift register. Here denotes: | Two new random sequences $\langle a_\nu \rangle$ and $\langle m_\nu \rangle$ are formed from the contents of the three-digit shift register. Here denotes: | ||
| − | * | + | * the "algebraic sum" $a_\nu$: |
:$$a_\nu=x_\nu+x_{\nu-1}+x_{\nu-2},$$ | :$$a_\nu=x_\nu+x_{\nu-1}+x_{\nu-2},$$ | ||
| − | * | + | *the "modulo–2 sum" $m_\nu$: |
:$$m_\nu=x_\nu\oplus x_{\nu-1}\oplus x_{\nu-2}.$$ | :$$m_\nu=x_\nu\oplus x_{\nu-1}\oplus x_{\nu-2}.$$ | ||
| − | |||
| − | |||
<br><br><br><br><br><br> | <br><br><br><br><br><br> | ||
| − | Hints: This exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Two-Dimensional_Random_Variables|Two-Dimensional Random Variables]]. | + | Hints: |
| − | <br clear=all> | + | *This exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Two-Dimensional_Random_Variables|Two-Dimensional Random Variables]]. |
| + | *Use the following table for moment calculation. | ||
| + | <br clear=all> | ||
===Questions=== | ===Questions=== | ||
| Line 37: | Line 39: | ||
| − | {Determine the | + | {Determine the 2D–PDF $f_{xm}(x_\nu, m_\nu)$. Based on the result, evaluate the following statements. |
|type="[]"} | |type="[]"} | ||
- The random variables $x_\nu$ and $m_\nu$ are statistically dependent. | - The random variables $x_\nu$ and $m_\nu$ are statistically dependent. | ||
| Line 51: | Line 53: | ||
| − | {Determine the 2D PDF $f_{am}(a_\nu, m_\nu)$ and the correlation coefficient $\rho_{am}$. Which of the following statements are true? | + | {Determine the 2D–PDF $f_{am}(a_\nu, m_\nu)$ and the correlation coefficient $\rho_{am}$. Which of the following statements are true? |
|type="[]"} | |type="[]"} | ||
+ The random variables $a_\nu$ and $m_\nu$ are statistically dependent. | + The random variables $a_\nu$ and $m_\nu$ are statistically dependent. | ||
| Line 64: | Line 66: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' It can be seen from the table | + | '''(1)''' It can be seen from the table in the information section that for the modulo–2 sum, the two values $0$ and $1$ have equal probability: |
:$${\rm Pr}(m_\nu = 0) = {\rm Pr}(m_\nu = 1)\hspace{0.15cm}\underline{=0.5}.$$ | :$${\rm Pr}(m_\nu = 0) = {\rm Pr}(m_\nu = 1)\hspace{0.15cm}\underline{=0.5}.$$ | ||
| − | '''(2)''' The table shows that for each preassignment ⇒ $( x_{\nu-1}, x_{\nu-2}) = (0,0), (0,1), (1,0), (1,1)$ the values $m_\nu = 0$ | + | '''(2)''' The table shows that for each preassignment ⇒ $( x_{\nu-1}, x_{\nu-2}) = (0,0), (0,1), (1,0), (1,1)$, the values $m_\nu = 0$ and $m_\nu = 1$ resp. are equally likely. |
*Expressed differently: ${\rm Pr}(m_{\nu}\hspace{0.05cm}|\hspace{0.05cm}m_{\nu-1}) = {\rm Pr}( m_{\nu}).$ | *Expressed differently: ${\rm Pr}(m_{\nu}\hspace{0.05cm}|\hspace{0.05cm}m_{\nu-1}) = {\rm Pr}( m_{\nu}).$ | ||
| − | *This exactly matches the definition of "statistical independence" ⇒ <u>Answer 1</u>. | + | *This exactly matches the definition of "statistical independence" ⇒ <u>Answer 1</u>. |
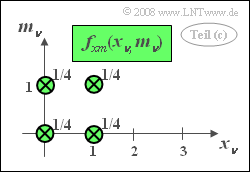
| − | [[File:P_ID224__Sto_A_4_3_c.png|right|frame|2D PDF of $x$ and $m$]] | + | [[File:P_ID224__Sto_A_4_3_c.png|right|frame|2D–PDF of $x$ and $m$]] |
| − | '''(3)''' Correct are <u>the second and the last suggested solutions</u>. | + | '''(3)''' Correct are <u>the second and the last suggested solutions</u>. |
| − | *The 2D PDF consists of four Dirac functions, each with weight $1/4$. | + | *The 2D–PDF consists of four Dirac delta functions, each with weight $1/4$. |
| − | *One obtains this result, for example, by evaluating the table | + | *One obtains this result, for example, by evaluating the table in the data section. |
| − | *Since $f_{xm}(x_\nu, m_\nu) | + | *Since $f_{xm}(x_\nu, m_\nu)=f_{x}(x_\nu) \cdot f_{m}(m_\nu)$, the quantities $x_\nu$ and $m_\nu$ are statistically independent. |
| − | *Statistically independent random variables, however, are also linearly statistically independent, so they are certainly uncorrelated. | + | *Statistically independent random variables, however, are also linearly statistically independent, so they are certainly uncorrelated. |
| Line 86: | Line 88: | ||
'''(4)''' Within the sequence $\langle a_\nu \rangle$ of algebraic sum there are statistical bindings ⇒ <u>Answer 2</u>. | '''(4)''' Within the sequence $\langle a_\nu \rangle$ of algebraic sum there are statistical bindings ⇒ <u>Answer 2</u>. | ||
| − | *You can see this because the unconditional probability $ {\rm Pr}( a_{\nu} = 0) =1/8$ | + | *You can see this because the unconditional probability is $ {\rm Pr}( a_{\nu} = 0) =1/8$, |
| − | *while, for example ${\rm Pr}(a_{\nu} = 0\hspace{0.05cm}|\hspace{0.05cm}a_{\nu-1} = 3) =0$ holds. | + | *while, for example, ${\rm Pr}(a_{\nu} = 0\hspace{0.05cm}|\hspace{0.05cm}a_{\nu-1} = 3) =0$ holds. |
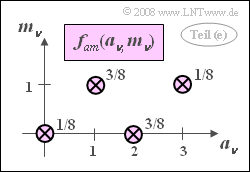
| − | [[File:P_ID225__Sto_A_4_3_e.png|right|frame|2D PDF of $a$ and $m$]] | + | [[File:P_ID225__Sto_A_4_3_e.png|right|frame|2D–PDF of $a$ and $m$]] |
| − | '''(5)''' Correct are <u>the first and the last suggested solutions</u>: | + | '''(5)''' Correct are <u>the first and the last suggested solutions</u>: |
| − | *As in the subtask '''(3)''' there are again four Dirac functions, but this time not with equal | + | *As in the subtask '''(3)''' there are again four Dirac delta functions, but this time not with equal Dirac weights $1/4$. |
*The two-dimensional PDF thus cannot be written as a product of the two marginal probability densities. | *The two-dimensional PDF thus cannot be written as a product of the two marginal probability densities. | ||
| − | *But this means that statistical bindings must exist between $a_\nu$ and $m_\nu$ | + | *But this means that statistical bindings must exist between $a_\nu$ and $m_\nu$. |
| − | *For the joint expected value, one obtains: | + | *For the joint expected value, one obtains: |
:$${\rm E}\big[a\cdot m \big] = \rm \frac{1}{8}\cdot 0 \cdot 0 +\frac{3}{8}\cdot 2 \cdot 0 +\frac{3}{8}\cdot 1 \cdot 1 + \frac{1}{8}\cdot 3 \cdot 1 = \frac{3}{4}.$$ | :$${\rm E}\big[a\cdot m \big] = \rm \frac{1}{8}\cdot 0 \cdot 0 +\frac{3}{8}\cdot 2 \cdot 0 +\frac{3}{8}\cdot 1 \cdot 1 + \frac{1}{8}\cdot 3 \cdot 1 = \frac{3}{4}.$$ | ||
| − | *With the linear means ${\rm E}\big[a \big] = 1.5$ and ${\rm E}[m] = 0.5$ it | + | *With the linear means ${\rm E}\big[a \big] = 1.5$ and ${\rm E}[m] = 0.5$ it follows for the covariance: |
:$$\mu_{am}= {\rm E}\big[ a\cdot m \big] - {\rm E}\big[ a \big]\cdot {\rm E} \big[ m \big] = \rm 0.75-1.5\cdot 0.5 = \rm 0.$$ | :$$\mu_{am}= {\rm E}\big[ a\cdot m \big] - {\rm E}\big[ a \big]\cdot {\rm E} \big[ m \big] = \rm 0.75-1.5\cdot 0.5 = \rm 0.$$ | ||
| − | *Thus, the correlation coefficient $\rho_{am}= 0$. That is | + | *Thus, the correlation coefficient $\rho_{am}= 0$. That is: The dependencies present are nonlinear. |
| − | *The quantities $a_\nu$ and $m_\nu$ are statistically dependent, but still uncorrelated. | + | *The quantities $a_\nu$ and $m_\nu$ are statistically dependent, but still uncorrelated. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 13:49, 17 November 2022
A "clocked" random number generator returns a sequence $\langle x_\nu \rangle$ of binary random numbers.
- It is assumed that the binary numbers $0$ and $1$ occur with equal probabilities and that the individual random numbers do not depend on each other.
- The random numbers $ x_\nu \in \{0, 1\}$ are entered into the first memory location of a shift register and shifted down one digit with each clock pulse.
Two new random sequences $\langle a_\nu \rangle$ and $\langle m_\nu \rangle$ are formed from the contents of the three-digit shift register. Here denotes:
- the "algebraic sum" $a_\nu$:
- $$a_\nu=x_\nu+x_{\nu-1}+x_{\nu-2},$$
- the "modulo–2 sum" $m_\nu$:
- $$m_\nu=x_\nu\oplus x_{\nu-1}\oplus x_{\nu-2}.$$
Hints:
- This exercise belongs to the chapter Two-Dimensional Random Variables.
- Use the following table for moment calculation.
Questions
Solution
(1) It can be seen from the table in the information section that for the modulo–2 sum, the two values $0$ and $1$ have equal probability:
- $${\rm Pr}(m_\nu = 0) = {\rm Pr}(m_\nu = 1)\hspace{0.15cm}\underline{=0.5}.$$
(2) The table shows that for each preassignment ⇒ $( x_{\nu-1}, x_{\nu-2}) = (0,0), (0,1), (1,0), (1,1)$, the values $m_\nu = 0$ and $m_\nu = 1$ resp. are equally likely.
- Expressed differently: ${\rm Pr}(m_{\nu}\hspace{0.05cm}|\hspace{0.05cm}m_{\nu-1}) = {\rm Pr}( m_{\nu}).$
- This exactly matches the definition of "statistical independence" ⇒ Answer 1.
(3) Correct are the second and the last suggested solutions.
- The 2D–PDF consists of four Dirac delta functions, each with weight $1/4$.
- One obtains this result, for example, by evaluating the table in the data section.
- Since $f_{xm}(x_\nu, m_\nu)=f_{x}(x_\nu) \cdot f_{m}(m_\nu)$, the quantities $x_\nu$ and $m_\nu$ are statistically independent.
- Statistically independent random variables, however, are also linearly statistically independent, so they are certainly uncorrelated.
(4) Within the sequence $\langle a_\nu \rangle$ of algebraic sum there are statistical bindings ⇒ Answer 2.
- You can see this because the unconditional probability is $ {\rm Pr}( a_{\nu} = 0) =1/8$,
- while, for example, ${\rm Pr}(a_{\nu} = 0\hspace{0.05cm}|\hspace{0.05cm}a_{\nu-1} = 3) =0$ holds.
(5) Correct are the first and the last suggested solutions:
- As in the subtask (3) there are again four Dirac delta functions, but this time not with equal Dirac weights $1/4$.
- The two-dimensional PDF thus cannot be written as a product of the two marginal probability densities.
- But this means that statistical bindings must exist between $a_\nu$ and $m_\nu$.
- For the joint expected value, one obtains:
- $${\rm E}\big[a\cdot m \big] = \rm \frac{1}{8}\cdot 0 \cdot 0 +\frac{3}{8}\cdot 2 \cdot 0 +\frac{3}{8}\cdot 1 \cdot 1 + \frac{1}{8}\cdot 3 \cdot 1 = \frac{3}{4}.$$
- With the linear means ${\rm E}\big[a \big] = 1.5$ and ${\rm E}[m] = 0.5$ it follows for the covariance:
- $$\mu_{am}= {\rm E}\big[ a\cdot m \big] - {\rm E}\big[ a \big]\cdot {\rm E} \big[ m \big] = \rm 0.75-1.5\cdot 0.5 = \rm 0.$$
- Thus, the correlation coefficient $\rho_{am}= 0$. That is: The dependencies present are nonlinear.
- The quantities $a_\nu$ and $m_\nu$ are statistically dependent, but still uncorrelated.