Difference between revisions of "Aufgaben:Exercise 4.3Z: Dirac-shaped "2D-PDF""
From LNTwww
| (4 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID257__Sto_Z_4_3.png|right|frame|Dirac-shaped 2D PDF]] | + | [[File:P_ID257__Sto_Z_4_3.png|right|frame|Dirac-shaped 2D– PDF]] |
| − | The graph shows the two-dimensional probability density function $f_{xy}(x, y)$ of | + | The graph shows the two-dimensional probability density function $f_{xy}(x, y)$ of two discrete random variables $x$, $y$. |
| − | *This 2D PDF consists of eight Dirac points, marked by crosses. The numerical values indicate the corresponding probabilities. | + | *This 2D–PDF consists of eight Dirac points, marked by crosses. |
| − | *It can be seen that both $x$ and $y$ can take all integer values between the limits $-2$ and $+2$ | + | *The numerical values indicate the corresponding probabilities. |
| + | *It can be seen that both $x$ and $y$ can take all integer values between the limits $-2$ and $+2$. | ||
*The variances of the two random variables are given as follows: $\sigma_x^2 = 2$, $\sigma_y^2 = 1.4$. | *The variances of the two random variables are given as follows: $\sigma_x^2 = 2$, $\sigma_y^2 = 1.4$. | ||
| − | |||
| − | |||
| − | |||
| Line 18: | Line 16: | ||
Hints: | Hints: | ||
*The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Two-Dimensional_Random_Variables|Two-Dimensional Random Variables]]. | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Two-Dimensional_Random_Variables|Two-Dimensional Random Variables]]. | ||
| − | *Reference is made to the chapter [[Theory_of_Stochastic_Signals/Moments_of_a_Discrete_Random_Variable|Moments of a Discrete Random Variable]] | + | *Reference is also made to the chapter [[Theory_of_Stochastic_Signals/Moments_of_a_Discrete_Random_Variable|Moments of a Discrete Random Variable]] |
| Line 28: | Line 26: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Which of the following statements are true regarding the random variable $x$ | + | {Which of the following statements are true regarding the random variable $x$? |
|type="[]"} | |type="[]"} | ||
+ The probabilities for $-2$, $-1$, $0$, $+1$ and $+2$ are equal. | + The probabilities for $-2$, $-1$, $0$, $+1$ and $+2$ are equal. | ||
+ The random variable $x$ is mean-free $(m_x = 0)$. | + The random variable $x$ is mean-free $(m_x = 0)$. | ||
| − | - The probability ${\rm Pr}(x \le 1) | + | - The probability ${\rm Pr}(x \le 1)=0.9$. |
| − | {Which of the following statements are true with respect to the random variable $y$ | + | {Which of the following statements are true with respect to the random variable $y$? |
|type="[]"} | |type="[]"} | ||
- The probabilities for $-2$, $-1$, $0$, $+1$ and $+2$ are equal. | - The probabilities for $-2$, $-1$, $0$, $+1$ and $+2$ are equal. | ||
+ The random variable $y$ is mean-free $(m_y = 0)$. | + The random variable $y$ is mean-free $(m_y = 0)$. | ||
| − | + The probability ${\rm Pr}(y \le 1) | + | + The probability ${\rm Pr}(y \le 1)=0.9$. |
| − | {Calculate the value of the two-dimensional CDF at location $(+1, +1)$. | + | {Calculate the value of the two-dimensional cumulative distribution function $\rm (CDF)$ at location $(+1, +1)$. |
|type="{}"} | |type="{}"} | ||
$F_{xy}(+1, +1) \ = \ $ { 0.8 3% } | $F_{xy}(+1, +1) \ = \ $ { 0.8 3% } | ||
| − | {Calculate the probability that $x \le 1$ holds, conditioned on $y \le 1$ simultaneously. | + | {Calculate the probability that $x \le 1$ holds, conditioned on $y \le 1$ simultaneously. |
|type="{}"} | |type="{}"} | ||
${\rm Pr}(x ≤ 1\hspace{0.05cm} | \hspace{0.05cm}y ≤ 1)\ = \ $ { 0.889 3% } | ${\rm Pr}(x ≤ 1\hspace{0.05cm} | \hspace{0.05cm}y ≤ 1)\ = \ $ { 0.889 3% } | ||
| Line 56: | Line 54: | ||
| − | {Calculate the correlation coefficient $\rho_{xy}$ | + | {Calculate the correlation coefficient $\rho_{xy}$. Give the equation of the correlation line $K(x)$ What is its angle to the $x$–axis? |
|type="{}"} | |type="{}"} | ||
$\rho_{xy}\ = \ $ { 0.707 3% } | $\rho_{xy}\ = \ $ { 0.707 3% } | ||
| Line 65: | Line 63: | ||
|type="[]"} | |type="[]"} | ||
- The random variables $x$ and $y$ are statistically independent. | - The random variables $x$ and $y$ are statistically independent. | ||
| − | + It can already be seen from the given 2D PDF that $x$ and $y$ are statistically dependent on each other. | + | + It can already be seen from the given 2D–PDF that $x$ and $y$ are statistically dependent on each other. |
+ From the calculated correlation coefficient $\rho_{xy}$ one can conclude the statistical dependence between $x$ and $y$ . | + From the calculated correlation coefficient $\rho_{xy}$ one can conclude the statistical dependence between $x$ and $y$ . | ||
| Line 74: | Line 72: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Correct are the <u>first two answers</u>: | + | '''(1)''' Correct are the <u>first two answers</u>: |
| − | *The marginal probability density function $f_{x}(x)$ is obtained from the 2D PDF $f_{xy}(x, y)$ by integration over $y$. | + | *The marginal probability density function $f_{x}(x)$ is obtained from the 2D–PDF $f_{xy}(x, y)$ by integration over $y$. |
*For all possible values $ x \in \{-2, -1, \ 0, +1, +2\}$ the probabilities are equal $0.2$. | *For all possible values $ x \in \{-2, -1, \ 0, +1, +2\}$ the probabilities are equal $0.2$. | ||
| − | *It holds ${\rm Pr}(x \le 1)= 0.8$ | + | *It holds ${\rm Pr}(x \le 1)= 0.8$. The mean is $m_x = 0$. |
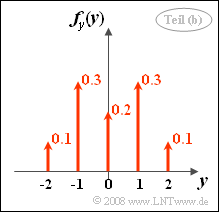
| − | [[File:P_ID258__Sto_Z_4_3_b.png|right|frame|Discrete marginal PDF $f_{y}(y)$]] | + | [[File:P_ID258__Sto_Z_4_3_b.png|right|frame|Discrete marginal PDF $f_{y}(y)$]] |
| − | '''(2)''' Correct are <u>the proposed solutions 2 and 3</u>: | + | '''(2)''' Correct are <u>the proposed solutions 2 and 3</u>: |
| − | *By integration over $x$ one obtains the PDF $f_{y}(y)$ sketched on the right. | + | *By integration over $x$ one obtains the PDF $f_{y}(y)$ sketched on the right. |
| − | *Due to symmetry, the mean value $m_y = 0$ is obtained. | + | *Due to symmetry, the mean value $m_y = 0$ is obtained. |
*The probability we are looking for is ${\rm Pr}(y \le 1)= 0.9$. | *The probability we are looking for is ${\rm Pr}(y \le 1)= 0.9$. | ||
| Line 94: | Line 92: | ||
*For $r_x = r_y = 1$ it follows: | *For $r_x = r_y = 1$ it follows: | ||
:$$F_{xy}(+1, +1) = {\rm Pr}\big [(x \le 1)\cap(y\le 1)\big ].$$ | :$$F_{xy}(+1, +1) = {\rm Pr}\big [(x \le 1)\cap(y\le 1)\big ].$$ | ||
| − | *As can be seen from the 2D PDF on the | + | *As can be seen from the 2D–PDF on the information page, this probability is ${\rm Pr}\big [(x \le 1)\cap(y\le 1)\big ]\hspace{0.15cm}\underline{=0.8}$. |
| − | '''(4)''' For this, Bayes' theorem can also be used to write: | + | '''(4)''' For this, Bayes' theorem can also be used to write: |
:$$ \rm Pr(\it x \le \rm 1)\hspace{0.05cm} | \hspace{0.05cm} \it y \le \rm 1) = \frac{ \rm Pr\big [(\it x \le \rm 1)\cap(\it y\le \rm 1)\big ]}{ \rm Pr(\it y\le \rm 1)} = \it \frac{F_{xy} \rm (1, \rm 1)}{F_{y}\rm (1)}.$$ | :$$ \rm Pr(\it x \le \rm 1)\hspace{0.05cm} | \hspace{0.05cm} \it y \le \rm 1) = \frac{ \rm Pr\big [(\it x \le \rm 1)\cap(\it y\le \rm 1)\big ]}{ \rm Pr(\it y\le \rm 1)} = \it \frac{F_{xy} \rm (1, \rm 1)}{F_{y}\rm (1)}.$$ | ||
| Line 108: | Line 106: | ||
:$$m_{xy} = {\rm E}\big[x\cdot y \big] = \sum\limits_{i} {\rm Pr}( x_i \cap y_i)\cdot x_i\cdot y_i. $$ | :$$m_{xy} = {\rm E}\big[x\cdot y \big] = \sum\limits_{i} {\rm Pr}( x_i \cap y_i)\cdot x_i\cdot y_i. $$ | ||
| − | *There remain five Dirac functions with $x_i \cdot y_i \ne 0$: | + | *There remain five Dirac delta functions with $x_i \cdot y_i \ne 0$: |
:$$m_{xy} = \rm 0.1\cdot (-2) (-1) + 0.2\cdot(-1) (-1)+ 0.2\cdot 1\cdot 1 + 0.1\cdot 2\cdot 1+ 0.1\cdot 2\cdot 2\hspace{0.15cm}\underline{=\rm 1.2}.$$ | :$$m_{xy} = \rm 0.1\cdot (-2) (-1) + 0.2\cdot(-1) (-1)+ 0.2\cdot 1\cdot 1 + 0.1\cdot 2\cdot 1+ 0.1\cdot 2\cdot 2\hspace{0.15cm}\underline{=\rm 1.2}.$$ | ||
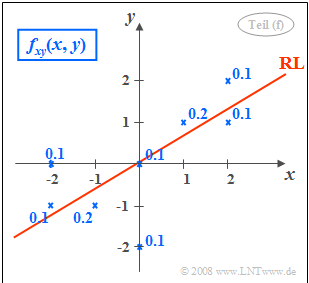
| − | [[File: | + | [[File:EN_Sto_Z_4_3_f.png|right|frame|2D–PDF and regression line $\rm (RL)$]] |
'''(6)''' For the correlation coefficient: | '''(6)''' For the correlation coefficient: | ||
:$$\rho_{xy} = \frac{\mu_{xy}}{\sigma_x\cdot \sigma_y} = \frac{1.2}{\sqrt{2}\cdot\sqrt{1.4}}\hspace{0.15cm}\underline{=0.717}.$$ | :$$\rho_{xy} = \frac{\mu_{xy}}{\sigma_x\cdot \sigma_y} = \frac{1.2}{\sqrt{2}\cdot\sqrt{1.4}}\hspace{0.15cm}\underline{=0.717}.$$ | ||
| Line 122: | Line 120: | ||
:$$y=\frac{\sigma_y}{\sigma_x}\cdot \rho_{xy}\cdot x = \frac{\mu_{xy}}{\sigma_x^{\rm 2}}\cdot x = \rm 0.6\cdot \it x.$$ | :$$y=\frac{\sigma_y}{\sigma_x}\cdot \rho_{xy}\cdot x = \frac{\mu_{xy}}{\sigma_x^{\rm 2}}\cdot x = \rm 0.6\cdot \it x.$$ | ||
| − | * | + | *See sketch on the right. The angle between the regression line $\rm (RL)$ and the $x$-axis is |
:$$\theta_{y\hspace{0.05cm}→\hspace{0.05cm} x} = \arctan(0.6) \hspace{0.15cm}\underline{=31^\circ}.$$ | :$$\theta_{y\hspace{0.05cm}→\hspace{0.05cm} x} = \arctan(0.6) \hspace{0.15cm}\underline{=31^\circ}.$$ | ||
| − | '''(7)''' The correct solutions are <u>solutions 2 and 3</u>: | + | '''(7)''' The correct solutions are <u>solutions 2 and 3</u>: |
| − | *If statistically independent, $f_{xy}(x, y) = f_{x}(x) \cdot f_{y}(y)$ should hold, which is not done here. | + | *If statistically independent, $f_{xy}(x, y) = f_{x}(x) \cdot f_{y}(y)$ should hold, which is not done here. |
*From correlatedness $($follows from $\rho_{xy} \ne 0)$ it is possible to directly infer statistical dependence, | *From correlatedness $($follows from $\rho_{xy} \ne 0)$ it is possible to directly infer statistical dependence, | ||
| − | *because correlation means a special form of statistical dependence, | + | *because correlation means a special form of statistical dependence, namely linear statistical dependence. |
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 16:41, 10 April 2022
The graph shows the two-dimensional probability density function $f_{xy}(x, y)$ of two discrete random variables $x$, $y$.
- This 2D–PDF consists of eight Dirac points, marked by crosses.
- The numerical values indicate the corresponding probabilities.
- It can be seen that both $x$ and $y$ can take all integer values between the limits $-2$ and $+2$.
- The variances of the two random variables are given as follows: $\sigma_x^2 = 2$, $\sigma_y^2 = 1.4$.
Hints:
- The exercise belongs to the chapter Two-Dimensional Random Variables.
- Reference is also made to the chapter Moments of a Discrete Random Variable
Questions
Solution
(1) Correct are the first two answers:
- The marginal probability density function $f_{x}(x)$ is obtained from the 2D–PDF $f_{xy}(x, y)$ by integration over $y$.
- For all possible values $ x \in \{-2, -1, \ 0, +1, +2\}$ the probabilities are equal $0.2$.
- It holds ${\rm Pr}(x \le 1)= 0.8$. The mean is $m_x = 0$.
(2) Correct are the proposed solutions 2 and 3:
- By integration over $x$ one obtains the PDF $f_{y}(y)$ sketched on the right.
- Due to symmetry, the mean value $m_y = 0$ is obtained.
- The probability we are looking for is ${\rm Pr}(y \le 1)= 0.9$.
(3) By definition:
- $$F_{xy}(r_x, r_y) = {\rm Pr} \big [(x \le r_x)\cap(y\le r_y)\big ].$$
- For $r_x = r_y = 1$ it follows:
- $$F_{xy}(+1, +1) = {\rm Pr}\big [(x \le 1)\cap(y\le 1)\big ].$$
- As can be seen from the 2D–PDF on the information page, this probability is ${\rm Pr}\big [(x \le 1)\cap(y\le 1)\big ]\hspace{0.15cm}\underline{=0.8}$.
(4) For this, Bayes' theorem can also be used to write:
- $$ \rm Pr(\it x \le \rm 1)\hspace{0.05cm} | \hspace{0.05cm} \it y \le \rm 1) = \frac{ \rm Pr\big [(\it x \le \rm 1)\cap(\it y\le \rm 1)\big ]}{ \rm Pr(\it y\le \rm 1)} = \it \frac{F_{xy} \rm (1, \rm 1)}{F_{y}\rm (1)}.$$
- With the results from (2) and (3) it follows $ \rm Pr(\it x \le \rm 1)\hspace{0.05cm} | \hspace{0.05cm} \it y \le \rm 1) = 0.8/0.9 = 8/9 \hspace{0.15cm}\underline{=0.889}$.
(5) According to the definition, the common moment is:
- $$m_{xy} = {\rm E}\big[x\cdot y \big] = \sum\limits_{i} {\rm Pr}( x_i \cap y_i)\cdot x_i\cdot y_i. $$
- There remain five Dirac delta functions with $x_i \cdot y_i \ne 0$:
- $$m_{xy} = \rm 0.1\cdot (-2) (-1) + 0.2\cdot(-1) (-1)+ 0.2\cdot 1\cdot 1 + 0.1\cdot 2\cdot 1+ 0.1\cdot 2\cdot 2\hspace{0.15cm}\underline{=\rm 1.2}.$$
(6) For the correlation coefficient:
- $$\rho_{xy} = \frac{\mu_{xy}}{\sigma_x\cdot \sigma_y} = \frac{1.2}{\sqrt{2}\cdot\sqrt{1.4}}\hspace{0.15cm}\underline{=0.717}.$$
- This takes into account that because $m_x = m_y = 0$ the covariance $\mu_{xy}$ is equal to the moment $m_{xy}$ .
- The equation of the correlation line is:
- $$y=\frac{\sigma_y}{\sigma_x}\cdot \rho_{xy}\cdot x = \frac{\mu_{xy}}{\sigma_x^{\rm 2}}\cdot x = \rm 0.6\cdot \it x.$$
- See sketch on the right. The angle between the regression line $\rm (RL)$ and the $x$-axis is
- $$\theta_{y\hspace{0.05cm}→\hspace{0.05cm} x} = \arctan(0.6) \hspace{0.15cm}\underline{=31^\circ}.$$
(7) The correct solutions are solutions 2 and 3:
- If statistically independent, $f_{xy}(x, y) = f_{x}(x) \cdot f_{y}(y)$ should hold, which is not done here.
- From correlatedness $($follows from $\rho_{xy} \ne 0)$ it is possible to directly infer statistical dependence,
- because correlation means a special form of statistical dependence, namely linear statistical dependence.