Difference between revisions of "Aufgaben:Exercise 4.4: Two-dimensional Gaussian PDF"
From LNTwww
| (4 intermediate revisions by the same user not shown) | |||
| Line 5: | Line 5: | ||
[[File:P_ID261__Sto_A_4_4_neu.png|right|frame|Table: Gaussian error functions]] | [[File:P_ID261__Sto_A_4_4_neu.png|right|frame|Table: Gaussian error functions]] | ||
We consider two-dimensional random variables, where both components are always assumed to be mean-free. | We consider two-dimensional random variables, where both components are always assumed to be mean-free. | ||
| − | *The | + | *The »two-dimensional probability density function« of the random variable $(u, v)$ is: |
:$$f_{uv}(u, v)={1}/{\pi} \cdot {\rm e}^{-(2u^{\rm 2} \hspace{0.05cm}+ \hspace{0.05cm}v^{\rm 2}\hspace{-0.05cm}/\rm 2)}.$$ | :$$f_{uv}(u, v)={1}/{\pi} \cdot {\rm e}^{-(2u^{\rm 2} \hspace{0.05cm}+ \hspace{0.05cm}v^{\rm 2}\hspace{-0.05cm}/\rm 2)}.$$ | ||
| − | * | + | *For another Gaussian two-dimensional random variable $(x, y)$ the following parameters are known: |
:$$\sigma_x= 0.5, \hspace{0.5cm}\sigma_y = 1,\hspace{0.5cm}\rho_{xy} = 1. $$ | :$$\sigma_x= 0.5, \hspace{0.5cm}\sigma_y = 1,\hspace{0.5cm}\rho_{xy} = 1. $$ | ||
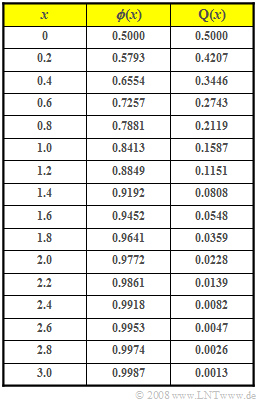
| − | * | + | *In the adjacent table can be found |
| + | #the values of the »Gaussian cumulative distribution function« ${\rm \phi}(x)$ and | ||
| + | #the »complementary function« ${\rm Q}(x) = 1- {\rm \phi}(x)$. | ||
| Line 17: | Line 19: | ||
Hints: | Hints: | ||
| − | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Two-Dimensional_Gaussian_Random_Variables|Two-dimensional Gaussian Random Variables]]. | + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Two-Dimensional_Gaussian_Random_Variables|»Two-dimensional Gaussian Random Variables«]]. |
| − | *Reference is also made to the chapter [[Theory_of_Stochastic_Signals/Gaussian_Distributed_Random_Variables|Gaussian distributed random variables | + | |
| − | + | *Reference is also made to the chapter [[Theory_of_Stochastic_Signals/Gaussian_Distributed_Random_Variables|»Gaussian distributed random variables«]]. | |
| − | |||
| − | |||
| Line 40: | Line 40: | ||
| − | {Calculate the probability that $u$ is less than $1$ | + | {Calculate the probability that $u$ is less than $1$. |
|type="{}"} | |type="{}"} | ||
${\rm Pr}(u < 1)\ = \ $ { 0.9772 3% } | ${\rm Pr}(u < 1)\ = \ $ { 0.9772 3% } | ||
| − | {Calculate the probability that the random variable $u$ is less than $1$ and at the same time the random variable $v$ is greater than $1$ | + | {Calculate the probability that the random variable $u$ is less than $1$ and at the same time the random variable $v$ is greater than $1$. |
|type="{}"} | |type="{}"} | ||
${\rm Pr}\big[(u < 1) ∩ (υ > 1)\big]\ = \ $ { 0.1551 3% } | ${\rm Pr}\big[(u < 1) ∩ (υ > 1)\big]\ = \ $ { 0.1551 3% } | ||
| Line 52: | Line 52: | ||
{Which of the statements are true for the two-dimensional random variable $(x, y)$? | {Which of the statements are true for the two-dimensional random variable $(x, y)$? | ||
|type="[]"} | |type="[]"} | ||
| − | + The joint | + | + The joint probability density function $f_{xy}(x, y)$ is always zero outside the straight line $y = 2x$. |
- For all pairs of values on the straight line $y = 2x$ holds: $f_{xy}(x, y)= 0.5$. | - For all pairs of values on the straight line $y = 2x$ holds: $f_{xy}(x, y)= 0.5$. | ||
+ With respect to the edge PDFs: $f_{x}(x) = f_{u}(u)$ and $f_{y}(y) = f_{v}(v)$ holds. | + With respect to the edge PDFs: $f_{x}(x) = f_{u}(u)$ and $f_{y}(y) = f_{v}(v)$ holds. | ||
| Line 73: | Line 73: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' <u>Both statements are true</u>: | '''(1)''' <u>Both statements are true</u>: | ||
| − | *Comparing the given 2D PDF with the general 2D PDF | + | *Comparing the given 2D–PDF with the general 2D–PDF |
| − | $$f_{uv}(u,v) = \frac{\rm 1}{{\rm 2}\it\pi \cdot \sigma_u \cdot \sigma_v \cdot \sqrt{{\rm 1}-\it \rho_{\it uv}^{\rm 2}}} \cdot \rm exp\left[\frac{\rm 1}{2\cdot (\rm 1-\it \rho_{uv}^{\rm 2}{\rm )}}(\frac{\it u^{\rm 2}}{\it\sigma_u^{\rm 2}} + \frac{\it v^{\rm 2}}{\it\sigma_v^{\rm 2}} - \rm 2\it\rho_{uv}\frac{\it u\cdot \it v}{\sigma_u\cdot \sigma_v}\rm )\right],$$ | + | :$$f_{uv}(u,v) = \frac{\rm 1}{{\rm 2}\it\pi \cdot \sigma_u \cdot \sigma_v \cdot \sqrt{{\rm 1}-\it \rho_{\it uv}^{\rm 2}}} \cdot \rm exp\left[\frac{\rm 1}{2\cdot (\rm 1-\it \rho_{uv}^{\rm 2}{\rm )}}(\frac{\it u^{\rm 2}}{\it\sigma_u^{\rm 2}} + \frac{\it v^{\rm 2}}{\it\sigma_v^{\rm 2}} - \rm 2\it\rho_{uv}\frac{\it u\cdot \it v}{\sigma_u\cdot \sigma_v}\rm )\right],$$ |
| − | :so it can be seen that no term with $u \cdot v$ occurs in the exponent, which is only possible with $\rho_{uv} = 0$ | + | :so it can be seen that no term with $u \cdot v$ occurs in the exponent, which is only possible with $\rho_{uv} = 0$. |
*But this means that $u$ and $v$ are uncorrelated. | *But this means that $u$ and $v$ are uncorrelated. | ||
| − | *For Gaussian random variables, however, statistical independence always follows from uncorrelatedness. | + | *For Gaussian random variables, however, statistical independence always follows from uncorrelatedness. |
'''(2)''' With statistical independence holds: | '''(2)''' With statistical independence holds: | ||
| − | :$$f_{uv}(u, v) = f_u(u)\cdot f_v(v) | + | :$$f_{uv}(u, v) = f_u(u)\cdot f_v(v) $$ |
| − | f_u(u)=\frac{{\rm e}^{-{\it u^{\rm 2}}/{(2\sigma_u^{\rm 2})}}}{\sqrt{\rm 2\pi}\cdot\sigma_u} , | + | :$$f_u(u)=\frac{{\rm e}^{-{\it u^{\rm 2}}/{(2\sigma_u^{\rm 2})}}}{\sqrt{\rm 2\pi}\cdot\sigma_u} , $$ |
| + | :$$\it f_v{\rm (}v{\rm )}=\frac{{\rm e}^{-{\it v^{\rm 2}}/{{\rm (}{\rm 2}\sigma_v^{\rm 2}{\rm )}}}}{\sqrt{\rm 2\pi}\cdot\sigma_v}.$$ | ||
| − | *By comparing coefficients, we get $\sigma_u = 0.5$ and $\sigma_v = 1$. | + | *By comparing coefficients, we get $\sigma_u = 0.5$ and $\sigma_v = 1$. |
*The quotient is thus $\sigma_u/\sigma_v\hspace{0.15cm}\underline{=0.5}$. | *The quotient is thus $\sigma_u/\sigma_v\hspace{0.15cm}\underline{=0.5}$. | ||
| − | + | '''(3)''' Because $u$ is a continuous random variable: | |
| − | '''(3)''' | ||
:$$\rm Pr(\it u < \rm 1) = \rm Pr(\it u \le \rm 1) =\it F_u\rm (1). $$ | :$$\rm Pr(\it u < \rm 1) = \rm Pr(\it u \le \rm 1) =\it F_u\rm (1). $$ | ||
| Line 99: | Line 99: | ||
| − | + | [[File:P_ID265__Sto_A_4_4_d.png|right|frame|$\rm Pr\big[(\it u < \rm 1) \cap (\it v > \rm 1)\big]$]] | |
'''(4)''' Due to the statistical independence between $u$ and $v$ holds: | '''(4)''' Due to the statistical independence between $u$ and $v$ holds: | ||
:$$\rm Pr\big[(\it u < \rm 1) \cap (\it v > \rm 1)\big] = \rm Pr(\it u < \rm 1)\cdot \rm Pr(\it v > \rm 1).$$ | :$$\rm Pr\big[(\it u < \rm 1) \cap (\it v > \rm 1)\big] = \rm Pr(\it u < \rm 1)\cdot \rm Pr(\it v > \rm 1).$$ | ||
| Line 108: | Line 108: | ||
:$$\Rightarrow \hspace{0.3cm} \rm Pr\big[(\it u < \rm 1) \cap (\it v > \rm 1)\big] = \rm 0.9772\cdot \rm 0.1587 \hspace{0.15cm}\underline{ = \rm 0.1551}.$$ | :$$\Rightarrow \hspace{0.3cm} \rm Pr\big[(\it u < \rm 1) \cap (\it v > \rm 1)\big] = \rm 0.9772\cdot \rm 0.1587 \hspace{0.15cm}\underline{ = \rm 0.1551}.$$ | ||
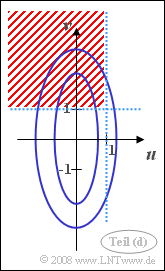
| − | The sketch illustrates the given constellation: | + | The sketch on the right illustrates the given constellation: |
| − | *The PDF (blue) | + | *The PDF contour lines (blue) are stretched ellipses due to $\sigma_v > \sigma_u$ in vertical direction. |
| − | *Drawn in red shading is the area whose probability should be calculated in this subtask. | + | *Drawn in red (shading) is the area whose probability should be calculated in this subtask. |
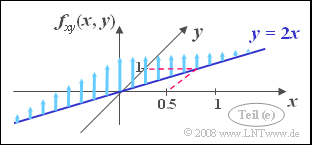
| − | [[File:P_ID266__Sto_A_4_4_e.png|right|frame| | + | [[File:P_ID266__Sto_A_4_4_e.png|right|frame|"Dirac wall" on the correlation line]] |
| − | '''(5)''' Correct are <u>the first and the third suggested solutions</u>: | + | '''(5)''' Correct are <u>the first and the third suggested solutions</u>: |
*Because $\rho_{xy} = 1$ there is a deterministic correlation between $x$ and $y$ | *Because $\rho_{xy} = 1$ there is a deterministic correlation between $x$ and $y$ | ||
| − | :⇒ All values lie on the straight line $y =K | + | :⇒ All values lie on the straight line $y =K \cdot x$. |
*Because of the standard deviations $\sigma_x = 0.5$ and $\sigma_y = 1$ it holds $K = 2$. | *Because of the standard deviations $\sigma_x = 0.5$ and $\sigma_y = 1$ it holds $K = 2$. | ||
| − | *On this straight line $y = 2x$ all PDF values are infinitely large. | + | *On this straight line $y = 2x$ ⇒ all PDF values are infinitely large. |
| − | *This means: The | + | *This means: The joint PDF is here a "Dirac wall". |
| − | *As you can see from the sketch, the PDF values are distributed | + | *As you can see from the sketch, the PDF values are Gaussian distributed on the straight line $y = 2x$. |
| − | + | *The two marginal probability densities are also Gaussian functions, each with zero mean. | |
| − | *The two marginal probability densities are also Gaussian functions, each with zero mean. | + | *Because of $\sigma_x = \sigma_u$ and $\sigma_y = \sigma_v$ also holds: |
| − | *Because $\sigma_x = \sigma_u$ and $\sigma_y = \sigma_v$ also holds: | ||
:$$f_x(x) = f_u(u), \hspace{0.5cm}f_y(y) = f_v(v).$$ | :$$f_x(x) = f_u(u), \hspace{0.5cm}f_y(y) = f_v(v).$$ | ||
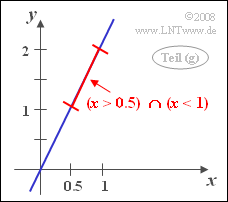
[[File:P_ID274__Sto_A_4_4_g.png|right|frame|Probability calculation for the Dirac wall]] | [[File:P_ID274__Sto_A_4_4_g.png|right|frame|Probability calculation for the Dirac wall]] | ||
| − | '''(6)''' Since the PDF of the random variable | + | '''(6)''' Since the PDF of the random variable $x$ is identical to the PDF $f_u(u)$, it also results in exactly the same probability as calculated in the subtask '''(3)''': |
:$$\rm Pr(\it x < \rm 1) \hspace{0.15cm}\underline{ = \rm 0.9772}.$$ | :$$\rm Pr(\it x < \rm 1) \hspace{0.15cm}\underline{ = \rm 0.9772}.$$ | ||
| Line 136: | Line 135: | ||
'''(7)''' The random event $y > 1$ is identical to the event $x > 0.5$. | '''(7)''' The random event $y > 1$ is identical to the event $x > 0.5$. | ||
*Thus, the wanted probability is equal to: | *Thus, the wanted probability is equal to: | ||
| − | :$$\rm Pr \big[(\it x | + | :$${\rm Pr}\big[(x < 1) ∩ (y > 1)\big] = \rm Pr \big[ (\it x < \rm 1)\cap (\it x > \rm 0.5) \big] = \it F_x \rm( 1) - \it F_x\rm (0.5). $$ |
| − | *With the standard deviation $\sigma_x = 0.5$ follows further: | + | *With the standard deviation $\sigma_x = 0.5$ it follows further: |
:$$\rm Pr \big[(\it x > \rm 0.5) \cap (\it x < \rm 1)\big] = \rm \phi(\rm 2) - \phi(1)=\rm 0.9772- \rm 0.8413\hspace{0.15cm}\underline{=\rm 0.1359}.$$ | :$$\rm Pr \big[(\it x > \rm 0.5) \cap (\it x < \rm 1)\big] = \rm \phi(\rm 2) - \phi(1)=\rm 0.9772- \rm 0.8413\hspace{0.15cm}\underline{=\rm 0.1359}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 17:37, 9 January 2024
We consider two-dimensional random variables, where both components are always assumed to be mean-free.
- The »two-dimensional probability density function« of the random variable $(u, v)$ is:
- $$f_{uv}(u, v)={1}/{\pi} \cdot {\rm e}^{-(2u^{\rm 2} \hspace{0.05cm}+ \hspace{0.05cm}v^{\rm 2}\hspace{-0.05cm}/\rm 2)}.$$
- For another Gaussian two-dimensional random variable $(x, y)$ the following parameters are known:
- $$\sigma_x= 0.5, \hspace{0.5cm}\sigma_y = 1,\hspace{0.5cm}\rho_{xy} = 1. $$
- In the adjacent table can be found
- the values of the »Gaussian cumulative distribution function« ${\rm \phi}(x)$ and
- the »complementary function« ${\rm Q}(x) = 1- {\rm \phi}(x)$.
Hints:
- The exercise belongs to the chapter »Two-dimensional Gaussian Random Variables«.
- Reference is also made to the chapter »Gaussian distributed random variables«.
Questions
Solution
(1) Both statements are true:
- Comparing the given 2D–PDF with the general 2D–PDF
- $$f_{uv}(u,v) = \frac{\rm 1}{{\rm 2}\it\pi \cdot \sigma_u \cdot \sigma_v \cdot \sqrt{{\rm 1}-\it \rho_{\it uv}^{\rm 2}}} \cdot \rm exp\left[\frac{\rm 1}{2\cdot (\rm 1-\it \rho_{uv}^{\rm 2}{\rm )}}(\frac{\it u^{\rm 2}}{\it\sigma_u^{\rm 2}} + \frac{\it v^{\rm 2}}{\it\sigma_v^{\rm 2}} - \rm 2\it\rho_{uv}\frac{\it u\cdot \it v}{\sigma_u\cdot \sigma_v}\rm )\right],$$
- so it can be seen that no term with $u \cdot v$ occurs in the exponent, which is only possible with $\rho_{uv} = 0$.
- But this means that $u$ and $v$ are uncorrelated.
- For Gaussian random variables, however, statistical independence always follows from uncorrelatedness.
(2) With statistical independence holds:
- $$f_{uv}(u, v) = f_u(u)\cdot f_v(v) $$
- $$f_u(u)=\frac{{\rm e}^{-{\it u^{\rm 2}}/{(2\sigma_u^{\rm 2})}}}{\sqrt{\rm 2\pi}\cdot\sigma_u} , $$
- $$\it f_v{\rm (}v{\rm )}=\frac{{\rm e}^{-{\it v^{\rm 2}}/{{\rm (}{\rm 2}\sigma_v^{\rm 2}{\rm )}}}}{\sqrt{\rm 2\pi}\cdot\sigma_v}.$$
- By comparing coefficients, we get $\sigma_u = 0.5$ and $\sigma_v = 1$.
- The quotient is thus $\sigma_u/\sigma_v\hspace{0.15cm}\underline{=0.5}$.
(3) Because $u$ is a continuous random variable:
- $$\rm Pr(\it u < \rm 1) = \rm Pr(\it u \le \rm 1) =\it F_u\rm (1). $$
- With the mean $m_u = 0$ and the standard deviation $\sigma_u = 0.5$ we get:
- $$\rm Pr(\it u < \rm 1) = \rm \phi({\rm 1}/{\it\sigma_u})= \rm \phi(\rm 2) \hspace{0.15cm}\underline{=\rm 0.9772}. $$
(4) Due to the statistical independence between $u$ and $v$ holds:
- $$\rm Pr\big[(\it u < \rm 1) \cap (\it v > \rm 1)\big] = \rm Pr(\it u < \rm 1)\cdot \rm Pr(\it v > \rm 1).$$
- The probability ${\rm Pr}(u < 1) =0.9772$ has already been calculated.
- For the second probability ${\rm Pr}(v > 1)$ holds for reasons of symmetry:
- $$\rm Pr(\it v > \rm 1) = \rm Pr(\it v \le \rm (-1) = \it F_v\rm (-1) = \rm \phi(\frac{\rm -1}{\it\sigma_v}) = \rm Q(1) =0.1587$$
- $$\Rightarrow \hspace{0.3cm} \rm Pr\big[(\it u < \rm 1) \cap (\it v > \rm 1)\big] = \rm 0.9772\cdot \rm 0.1587 \hspace{0.15cm}\underline{ = \rm 0.1551}.$$
The sketch on the right illustrates the given constellation:
- The PDF contour lines (blue) are stretched ellipses due to $\sigma_v > \sigma_u$ in vertical direction.
- Drawn in red (shading) is the area whose probability should be calculated in this subtask.
(5) Correct are the first and the third suggested solutions:
- Because $\rho_{xy} = 1$ there is a deterministic correlation between $x$ and $y$
- ⇒ All values lie on the straight line $y =K \cdot x$.
- Because of the standard deviations $\sigma_x = 0.5$ and $\sigma_y = 1$ it holds $K = 2$.
- On this straight line $y = 2x$ ⇒ all PDF values are infinitely large.
- This means: The joint PDF is here a "Dirac wall".
- As you can see from the sketch, the PDF values are Gaussian distributed on the straight line $y = 2x$.
- The two marginal probability densities are also Gaussian functions, each with zero mean.
- Because of $\sigma_x = \sigma_u$ and $\sigma_y = \sigma_v$ also holds:
- $$f_x(x) = f_u(u), \hspace{0.5cm}f_y(y) = f_v(v).$$
(6) Since the PDF of the random variable $x$ is identical to the PDF $f_u(u)$, it also results in exactly the same probability as calculated in the subtask (3):
- $$\rm Pr(\it x < \rm 1) \hspace{0.15cm}\underline{ = \rm 0.9772}.$$
(7) The random event $y > 1$ is identical to the event $x > 0.5$.
- Thus, the wanted probability is equal to:
- $${\rm Pr}\big[(x < 1) ∩ (y > 1)\big] = \rm Pr \big[ (\it x < \rm 1)\cap (\it x > \rm 0.5) \big] = \it F_x \rm( 1) - \it F_x\rm (0.5). $$
- With the standard deviation $\sigma_x = 0.5$ it follows further:
- $$\rm Pr \big[(\it x > \rm 0.5) \cap (\it x < \rm 1)\big] = \rm \phi(\rm 2) - \phi(1)=\rm 0.9772- \rm 0.8413\hspace{0.15cm}\underline{=\rm 0.1359}.$$