Difference between revisions of "Aufgaben:Exercise 4.12Z: White Gaussian Noise"
m (Guenter moved page Aufgabe 4.12Z: Weißes Rauschen to Exercise 4.12Z: White Gaussian Noise) |
|||
| (6 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Power-Spectral_Density |
}} | }} | ||
| − | [[File:P_ID409__Sto_Z_4_12.png|right|frame| | + | [[File:P_ID409__Sto_Z_4_12.png|right|frame|PSD of white noise]] |
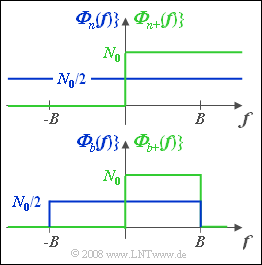
| − | + | A noise signal $n(t)$ is called "white" if it contains all spectral components without preference of any frequencies. | |
| − | * | + | * The physical power-spectral density defined only for positive frequencies ⇒ ${\it \Phi}_{n+}(f)$ is constant $($equal $N_0)$ and extends frequency-wise to infinity. |
| − | * ${\it \Phi}_{n+}(f)$ | + | * ${\it \Phi}_{n+}(f)$ is shown in green in the upper graph. The plus sign in the index is to indicate that the function is valid only for positive values of $f$. |
| − | * | + | * For mathematical description one usually uses the two-sided power-spectral density ${\it \Phi}_{n}(f)$. Here applies for all frequencies from $-\infty$ to $+\infty$ (blue curve in the upper graph): |
:$${\it \Phi}_n (f) ={N_0}/{2}.$$ | :$${\it \Phi}_n (f) ={N_0}/{2}.$$ | ||
| − | + | The bottom graph shows the two power-spectral densities ${\it \Phi}_{b}(f)$ and ${\it \Phi}_{b+}(f)$ of bandlimited white noise signal $b(t)$. It holds with the one-sided bandwidth $B$: | |
| − | :$${\it \Phi}_b(f)=\left\{ {N_0/2\atop 0}{\hspace{0.5cm} {\rm | + | :$${\it \Phi}_b(f)=\left\{ {N_0/2\atop 0}{\hspace{0.5cm} {\rm for}\quad |f|\le B \atop {\rm else}}\right.,$$ |
| − | :$${\it \Phi}_{b+}(f)=\left\{ {N_0\atop 0}{\hspace{0.5cm} {\rm | + | :$${\it \Phi}_{b+}(f)=\left\{ {N_0\atop 0}{\hspace{0.5cm} {\rm for}\quad 0 \le f\le B \atop {\rm else}}\right.$$ |
| − | + | For computer simulation of noise processes, band-limited noise must always be assumed, since only discrete-time processes can be handled. For this, the [[Signal_Representation/Discrete-Time_Signal_Representation#Sampling_theorem|Sampling Theorem]] must be obeyed. This states that the bandwidth $B$ must be set according to the interpolation distance $T_{\rm A}$ of the simulation. | |
| − | + | Assume the following numerical values throughout this exercise: | |
| − | * | + | * The noise power density – with respect to the resistor $1 \hspace{0.05cm}\rm \Omega$ – is $N_0 = 4 \cdot 10^{-14}\hspace{0.05cm}\rm V^2/Hz$. |
| − | * | + | * The (one-sided) bandwidth of the band-limited white noise is $B = 100 \hspace{0.08cm}\rm MHz$. |
| Line 27: | Line 27: | ||
| − | + | Hints: | |
| − | * | + | *This exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Power-Spectral_Density|Power-Spectral Density]]. |
| − | * | + | *Reference is also made to the chapter [[Theory_of_Stochastic_Signals/Auto-Correlation_Function|Auto-Correlation Function]]. |
| − | * | + | *The properties of white noise are summarized in the second part of the (German language) learning video [[Der_AWGN-Kanal_(Lernvideo)|The AWGN channel]]. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which statements are always true for a white noise signal $n(t)$. Give reasons for your answers. |
|type="[]"} | |type="[]"} | ||
| − | - | + | - The ACF $\varphi_n(t)$ has a sinc-shaped progression. |
| − | + | + | + The ACF $\varphi_n(\tau)$ is a Dirac delta function at $\tau = 0$ with weight $N_0/2$. |
| − | + In | + | + In practice, there is no (exact) white noise. |
| − | + | + | + Thermal noise can always be approximated as white. |
| − | - | + | - White noise is always Gaussian distributed. |
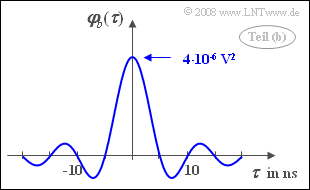
| − | { | + | {Calculate the ACF $\varphi_b(\tau)$ of the random signal $b(t)$ bandlimited to $B = 100 \hspace{0.08cm}\rm MHz$. What value results for $\tau = 0$? |
|type="{}"} | |type="{}"} | ||
| − | $\varphi_b(\ | + | $\varphi_b(\tau = 0) \ = \ $ { 4 3% } $\ \cdot 10^{-6} \ \rm V^2$ |
| − | { | + | {What is the rms value of this bandlimited random signal $b(t)$? |
|type="{}"} | |type="{}"} | ||
| − | $\sigma_b \ = \ $ { 2 3% } | + | $\sigma_b \ = \ $ { 2 3% } $\ \rm mV$ |
| − | { | + | {What sampling distance $T_{\rm A}$ should be (at most) chosen if the band-limited signal $b(t)$ is used for discrete-time simulation of white noise? |
|type="{}"} | |type="{}"} | ||
| − | $T_{\rm A} \ = | + | $T_{\rm A} \ = \ $ { 5 3% } $\ \rm ns$ |
| − | { | + | {Assume sampling distance $T_{\rm A} = 1 \hspace{0.05cm}\rm ns$. Then, which of the statements are true for two consecutive samples of the signal $b(t)$ ? |
| − | |type=" | + | |type="()"} |
| − | - | + | - The samples are uncorrelated. |
| − | + | + | + The samples are positively correlated. |
| − | - | + | - The samples are negatively correlated. |
| Line 72: | Line 72: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Correct are the <u>solutions 2, 3, and 4</u>: |
| − | * | + | *The auto-correlation function $\rm (ACF)$ is the Fourier transform of the power-spectral density $\rm (PSD)$. Here: |
| − | :$${\it \Phi}_n (f) = | + | :$${\it \Phi}_n (f) = {N_0}/{2} \hspace{0.3cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.3cm} \varphi_n (\tau)={N_0}/{2} \cdot {\rm \delta} ( \tau).$$ |
| − | * | + | *However, there is no "real" white noise in physics, since such a noise would have to have an infinitely large signal power $($the integral over the PSD as well as the ACF value at $\tau = 0$ are both infinitely large$)$. |
| − | * | + | *Thermal noise has a constant PSD up to frequencies of about $\text{6000 GHz}$. Since all (current) transmission systems operate in a much lower frequency range, thermal noise can be said to be "white" to a good approximation. |
| − | * | + | *The statistical property "white" says nothing about the amplitude distribution, which is determined by the probability density function $\rm (PDF)$ alone. |
| − | * | + | *When considering the phase of a bandpass signal as the stochastic variable, it is often modeled as uniformly distributed between $0$ and $2\pi$. |
| − | * | + | *If there are no statistical bindings between the respective phase angles at different times, this random process is also "white". |
| − | |||
| − | [[File:P_ID410__Sto_Z_4_12_b.png|right|frame| | + | [[File:P_ID410__Sto_Z_4_12_b.png|right|frame|ACF of band-limited noise]] |
| − | '''(2)''' | + | '''(2)''' The power-spectral density is a rectangle of width $2B$ and height $N_0/2$. |
| − | * | + | *The inverse Fourier transform yields an sinc–function: |
:$$\varphi_b(\tau) = N_0 \cdot B \cdot {\rm si} (2 \pi B \tau)\hspace{0.3cm} | :$$\varphi_b(\tau) = N_0 \cdot B \cdot {\rm si} (2 \pi B \tau)\hspace{0.3cm} | ||
\Rightarrow \hspace{0.3cm}\varphi_b(\tau = 0) = N_0 \cdot B \hspace{0.15cm}\underline {=4}\cdot 10^{-6} \ \rm V^2.$$ | \Rightarrow \hspace{0.3cm}\varphi_b(\tau = 0) = N_0 \cdot B \hspace{0.15cm}\underline {=4}\cdot 10^{-6} \ \rm V^2.$$ | ||
| Line 93: | Line 92: | ||
| − | '''(3)''' | + | '''(3)''' The ACF value at the point $\tau = 0$ gives the power. |
| − | * | + | *The root of this is called the "rms value": |
:$$\sigma_b = \sqrt{\varphi_b(\tau = 0)} \hspace{0.15cm}\underline {=2 \hspace{0.05cm}\rm V}.$$ | :$$\sigma_b = \sqrt{\varphi_b(\tau = 0)} \hspace{0.15cm}\underline {=2 \hspace{0.05cm}\rm V}.$$ | ||
| − | |||
| − | '''(4)''' | + | |
| − | * | + | '''(4)''' The ACF computed in '''(3)''' has zeros at equidistant distance from $T_{\rm A}= 1/(2B)\hspace{0.15cm}\underline {=5\hspace{0.05cm} \rm ns}$: |
| − | * | + | *There are no statistical bindings between the two signal values $b(t)$ and $b(t + \nu \cdot T_{\rm A})$, |
| + | *where $\nu$ can take all integer values. | ||
| − | '''(5)''' | + | '''(5)''' The correct solution is the <u>suggested solution 2</u>. |
| − | * | + | *The ACF value at $\tau = T_{\rm A} = 1 \hspace{0.05cm}\rm ns$ is |
| − | :$$\varphi_b(\tau = T_{\rm A}) = {\rm 4 \cdot 10^{-6} \hspace{0.1cm}V^2 \cdot | + | :$$\varphi_b(\tau = T_{\rm A}) = {\rm 4 \cdot 10^{-6} \hspace{0.1cm}V^2 \cdot sinc (1/5) \approx 3.742 \cdot 10^{-6} \hspace{0.1cm}V^2} > 0.$$ |
| − | * | + | *This result says: Two signal values separated by $T_{\rm A} = 1 \hspace{0.05cm}\rm ns$ are positively correlated: |
| − | * | + | :*If $b(t)$ is positive and large, then with high probability $b(t+1 \hspace{0.05cm}\rm ns)$ is also positive and large. |
| − | * | + | :*In contrast, there is a negative correlation between $b(t)$ and $b(t+7 \hspace{0.05cm}\rm ns)$. If $b(t)$ is positive, then $b(t+7 \hspace{0.05cm}\rm ns)$ is probably negative. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category:Theory of Stochastic Signals: Exercises|^4.5 | + | [[Category:Theory of Stochastic Signals: Exercises|^4.5 Power-Spectral Density^]] |
Latest revision as of 15:27, 25 March 2022
A noise signal $n(t)$ is called "white" if it contains all spectral components without preference of any frequencies.
- The physical power-spectral density defined only for positive frequencies ⇒ ${\it \Phi}_{n+}(f)$ is constant $($equal $N_0)$ and extends frequency-wise to infinity.
- ${\it \Phi}_{n+}(f)$ is shown in green in the upper graph. The plus sign in the index is to indicate that the function is valid only for positive values of $f$.
- For mathematical description one usually uses the two-sided power-spectral density ${\it \Phi}_{n}(f)$. Here applies for all frequencies from $-\infty$ to $+\infty$ (blue curve in the upper graph):
- $${\it \Phi}_n (f) ={N_0}/{2}.$$
The bottom graph shows the two power-spectral densities ${\it \Phi}_{b}(f)$ and ${\it \Phi}_{b+}(f)$ of bandlimited white noise signal $b(t)$. It holds with the one-sided bandwidth $B$:
- $${\it \Phi}_b(f)=\left\{ {N_0/2\atop 0}{\hspace{0.5cm} {\rm for}\quad |f|\le B \atop {\rm else}}\right.,$$
- $${\it \Phi}_{b+}(f)=\left\{ {N_0\atop 0}{\hspace{0.5cm} {\rm for}\quad 0 \le f\le B \atop {\rm else}}\right.$$
For computer simulation of noise processes, band-limited noise must always be assumed, since only discrete-time processes can be handled. For this, the Sampling Theorem must be obeyed. This states that the bandwidth $B$ must be set according to the interpolation distance $T_{\rm A}$ of the simulation.
Assume the following numerical values throughout this exercise:
- The noise power density – with respect to the resistor $1 \hspace{0.05cm}\rm \Omega$ – is $N_0 = 4 \cdot 10^{-14}\hspace{0.05cm}\rm V^2/Hz$.
- The (one-sided) bandwidth of the band-limited white noise is $B = 100 \hspace{0.08cm}\rm MHz$.
Hints:
- This exercise belongs to the chapter Power-Spectral Density.
- Reference is also made to the chapter Auto-Correlation Function.
- The properties of white noise are summarized in the second part of the (German language) learning video The AWGN channel.
Questions
Solution
- The auto-correlation function $\rm (ACF)$ is the Fourier transform of the power-spectral density $\rm (PSD)$. Here:
- $${\it \Phi}_n (f) = {N_0}/{2} \hspace{0.3cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.3cm} \varphi_n (\tau)={N_0}/{2} \cdot {\rm \delta} ( \tau).$$
- However, there is no "real" white noise in physics, since such a noise would have to have an infinitely large signal power $($the integral over the PSD as well as the ACF value at $\tau = 0$ are both infinitely large$)$.
- Thermal noise has a constant PSD up to frequencies of about $\text{6000 GHz}$. Since all (current) transmission systems operate in a much lower frequency range, thermal noise can be said to be "white" to a good approximation.
- The statistical property "white" says nothing about the amplitude distribution, which is determined by the probability density function $\rm (PDF)$ alone.
- When considering the phase of a bandpass signal as the stochastic variable, it is often modeled as uniformly distributed between $0$ and $2\pi$.
- If there are no statistical bindings between the respective phase angles at different times, this random process is also "white".
(2) The power-spectral density is a rectangle of width $2B$ and height $N_0/2$.
- The inverse Fourier transform yields an sinc–function:
- $$\varphi_b(\tau) = N_0 \cdot B \cdot {\rm si} (2 \pi B \tau)\hspace{0.3cm} \Rightarrow \hspace{0.3cm}\varphi_b(\tau = 0) = N_0 \cdot B \hspace{0.15cm}\underline {=4}\cdot 10^{-6} \ \rm V^2.$$
(3) The ACF value at the point $\tau = 0$ gives the power.
- The root of this is called the "rms value":
- $$\sigma_b = \sqrt{\varphi_b(\tau = 0)} \hspace{0.15cm}\underline {=2 \hspace{0.05cm}\rm V}.$$
(4) The ACF computed in (3) has zeros at equidistant distance from $T_{\rm A}= 1/(2B)\hspace{0.15cm}\underline {=5\hspace{0.05cm} \rm ns}$:
- There are no statistical bindings between the two signal values $b(t)$ and $b(t + \nu \cdot T_{\rm A})$,
- where $\nu$ can take all integer values.
(5) The correct solution is the suggested solution 2.
- The ACF value at $\tau = T_{\rm A} = 1 \hspace{0.05cm}\rm ns$ is
- $$\varphi_b(\tau = T_{\rm A}) = {\rm 4 \cdot 10^{-6} \hspace{0.1cm}V^2 \cdot sinc (1/5) \approx 3.742 \cdot 10^{-6} \hspace{0.1cm}V^2} > 0.$$
- This result says: Two signal values separated by $T_{\rm A} = 1 \hspace{0.05cm}\rm ns$ are positively correlated:
- If $b(t)$ is positive and large, then with high probability $b(t+1 \hspace{0.05cm}\rm ns)$ is also positive and large.
- In contrast, there is a negative correlation between $b(t)$ and $b(t+7 \hspace{0.05cm}\rm ns)$. If $b(t)$ is positive, then $b(t+7 \hspace{0.05cm}\rm ns)$ is probably negative.