Difference between revisions of "Aufgaben:Exercise 3.2: Spectrum with Angle Modulation"
m (→Solution) |
|||
| (3 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Modulation_Methods/Phase_Modulation_(PM) |
}} | }} | ||
| Line 7: | Line 7: | ||
* Source signal: | * Source signal: | ||
:$$q(t) = 2\,{\rm V} \cdot \sin(2 \pi \cdot 3\,{\rm kHz} \cdot t)\hspace{0.05cm},$$ | :$$q(t) = 2\,{\rm V} \cdot \sin(2 \pi \cdot 3\,{\rm kHz} \cdot t)\hspace{0.05cm},$$ | ||
| − | * | + | * Transmitted signal: |
:$$s(t) = 1\,{\rm V} \cdot \cos\hspace{-0.1cm}\big[2 \pi \cdot 100\,{\rm kHz} \cdot t + K_{\rm M} \cdot q(t)\big ]\hspace{0.05cm},$$ | :$$s(t) = 1\,{\rm V} \cdot \cos\hspace{-0.1cm}\big[2 \pi \cdot 100\,{\rm kHz} \cdot t + K_{\rm M} \cdot q(t)\big ]\hspace{0.05cm},$$ | ||
* Received signal (ideal channel): | * Received signal (ideal channel): | ||
| Line 77: | Line 77: | ||
| − | '''(2)''' An angle | + | '''(2)''' An angle modulation (PM, FM) always results in nonlinear distortion when the channel is bandlimited. |
*In contrast, double-sideband amplitude modulation (DSB-AM) here enables distortion-free transmission with $B_{\rm K} = 6 \ \rm kHz$ ; ⇒ <u>Answer 1</u>. | *In contrast, double-sideband amplitude modulation (DSB-AM) here enables distortion-free transmission with $B_{\rm K} = 6 \ \rm kHz$ ; ⇒ <u>Answer 1</u>. | ||
| Line 100: | Line 100: | ||
:$$S_{\rm TP}(f = 0) = 0.765\,{\rm V} \cdot \delta (f) \hspace{0.05cm}.$$ | :$$S_{\rm TP}(f = 0) = 0.765\,{\rm V} \cdot \delta (f) \hspace{0.05cm}.$$ | ||
*This is therefore infinite due to the Dirac function, and only the weight of the Dirac function is finite. | *This is therefore infinite due to the Dirac function, and only the weight of the Dirac function is finite. | ||
| − | *The same applies for all discrete spectral | + | *The same applies for all discrete spectral lines. |
| − | '''(5)''' $S_+(f)$ | + | '''(5)''' $S_+(f)$ is obtained from $S_{\rm TP}(f)$ by shifting $f_{\rm T}$ to the right. Therefore |
:$$S_{\rm +}(f = 97\,{\rm kHz}) = S_{\rm TP}(f = -3\,{\rm kHz}) \hspace{0.15cm}\underline {=-0.440\,{\rm V}} \hspace{0.05cm}.$$ | :$$S_{\rm +}(f = 97\,{\rm kHz}) = S_{\rm TP}(f = -3\,{\rm kHz}) \hspace{0.15cm}\underline {=-0.440\,{\rm V}} \hspace{0.05cm}.$$ | ||
| − | * | + | *The actual spectrum differs from $S_+(f)$ by a factor of $1/2$ at positive frequencies: |
:$$S(f = 97\,{\rm kHz}) = {1}/{2} \cdot S_{\rm +}(f = 97\,{\rm kHz}) \hspace{0.15cm}\underline {=-0.220\,{\rm V}} \hspace{0.05cm}.$$ | :$$S(f = 97\,{\rm kHz}) = {1}/{2} \cdot S_{\rm +}(f = 97\,{\rm kHz}) \hspace{0.15cm}\underline {=-0.220\,{\rm V}} \hspace{0.05cm}.$$ | ||
| − | * | + | *In general, we can write: |
:$$ S(f) = \frac{A_{\rm T}}{2} \cdot \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot \delta (f \pm (f_{\rm T}+ n \cdot f_{\rm N}))\hspace{0.05cm}.$$ | :$$ S(f) = \frac{A_{\rm T}}{2} \cdot \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot \delta (f \pm (f_{\rm T}+ n \cdot f_{\rm N}))\hspace{0.05cm}.$$ | ||
| − | '''(6)''' | + | '''(6)''' Under the suggested conditions, all the Bessel lines ${\rm J}_{|n|>3}$ can be disregarded. |
| − | * | + | * This gives $B_{\rm K} = 2 · 3 · f_{\rm N}\hspace{0.15cm}\underline { = 18 \ \rm kHz}$. |
| − | '''(7)''' | + | '''(7)''' The numerical values in the table given on the exercise page show that the following channel bandwidths would now be required: |
*für $η = 2$: $B_{\rm K} \hspace{0.15cm}\underline { = 24 \ \rm kHz}$, | *für $η = 2$: $B_{\rm K} \hspace{0.15cm}\underline { = 24 \ \rm kHz}$, | ||
*für $η = 3$: $B_{\rm K} \hspace{0.15cm}\underline { = 36 \ \rm kHz}$. | *für $η = 3$: $B_{\rm K} \hspace{0.15cm}\underline { = 36 \ \rm kHz}$. | ||
Latest revision as of 16:21, 23 January 2023
The following equations are assumed here:
- Source signal:
- $$q(t) = 2\,{\rm V} \cdot \sin(2 \pi \cdot 3\,{\rm kHz} \cdot t)\hspace{0.05cm},$$
- Transmitted signal:
- $$s(t) = 1\,{\rm V} \cdot \cos\hspace{-0.1cm}\big[2 \pi \cdot 100\,{\rm kHz} \cdot t + K_{\rm M} \cdot q(t)\big ]\hspace{0.05cm},$$
- Received signal (ideal channel):
- $$r(t) = s(t) = 1\,{\rm V} \cdot \cos\hspace{-0.1cm}\big[2 \pi \cdot 100\,{\rm kHz} \cdot t + \phi(t)\big ]\hspace{0.05cm},$$
- ideal demodulator:
- $$ v(t) = \frac{1}{ K_{\rm M}} \cdot \phi(t)\hspace{0.05cm}.$$
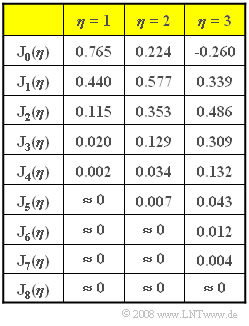
The graphs shows the $n$–th order Bessel functions of the first kind ${\rm J}_n (\eta)$ in table form.
Hints:
- This exercise belongs to the chapter Phase Modulation.
- Particular reference is made to the pages Spectral function of a phase-modulated sine signal and Interpretation of the Bessel spectrum.
Questions
Solution
(2) An angle modulation (PM, FM) always results in nonlinear distortion when the channel is bandlimited.
- In contrast, double-sideband amplitude modulation (DSB-AM) here enables distortion-free transmission with $B_{\rm K} = 6 \ \rm kHz$ ; ⇒ Answer 1.
(3) The modulation index (or phase deviation) is equal to $η = K_{\rm M} · A_{\rm N}$ for phase modulation.
- Thus, the modulator constant must be set to $K_{\rm M} = 1/A_{\rm N}\hspace{0.15cm}\underline { = 0.5 \rm \cdot {1}/{V}}$ to give $η = 1$ .
(4) A so-called Bessel spectrum is present:
- $$ S_{\rm TP}(f) = A_{\rm T} \cdot \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot \delta (f - n \cdot f_{\rm N})\hspace{0.05cm}.$$
- This is a discrete spectrum with components at $f = n · f_{\rm N}$, where $n$ is an integer.
- The weights of the Dirac functions are given by the Bessel functions. When $A_{\rm T} = 1\ \rm V$ , one obtains:
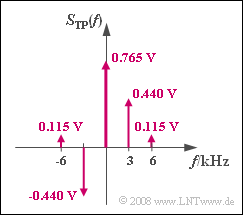
- $$ S_{\rm TP}(f = 0) = A_{\rm T} \cdot {\rm J}_0 (\eta = 1) \hspace{0.15cm}\underline {= 0.765\,{\rm V}},$$
- $$ S_{\rm TP}(f = f_{\rm N}) = A_{\rm T} \cdot {\rm J}_1 (\eta = 1)\hspace{0.15cm} = 0.440\,{\rm V},$$
- $$ S_{\rm TP}(f = 2 \cdot f_{\rm N}) = A_{\rm T} \cdot {\rm J}_2 (\eta = 1) = 0.115\,{\rm V} \hspace{0.05cm}.$$
- Due to the symmetry ${\rm J}_{-n} (\eta) = (-1)^n \cdot {\rm J}_{n} (\eta)$ , the spectral line at $f = -3 \ \rm kHz$ is obtained as:
- $$S_{\rm TP}(f = -f_{\rm N}) = -S_{\rm TP}(f = +f_{\rm N}) =\hspace{-0.01cm}\underline { -0.440\,{\rm V} \hspace{0.05cm}}.$$
Note: For the spectral value at $f = 0$ we should actually write:
- $$S_{\rm TP}(f = 0) = 0.765\,{\rm V} \cdot \delta (f) \hspace{0.05cm}.$$
- This is therefore infinite due to the Dirac function, and only the weight of the Dirac function is finite.
- The same applies for all discrete spectral lines.
(5) $S_+(f)$ is obtained from $S_{\rm TP}(f)$ by shifting $f_{\rm T}$ to the right. Therefore
- $$S_{\rm +}(f = 97\,{\rm kHz}) = S_{\rm TP}(f = -3\,{\rm kHz}) \hspace{0.15cm}\underline {=-0.440\,{\rm V}} \hspace{0.05cm}.$$
- The actual spectrum differs from $S_+(f)$ by a factor of $1/2$ at positive frequencies:
- $$S(f = 97\,{\rm kHz}) = {1}/{2} \cdot S_{\rm +}(f = 97\,{\rm kHz}) \hspace{0.15cm}\underline {=-0.220\,{\rm V}} \hspace{0.05cm}.$$
- In general, we can write:
- $$ S(f) = \frac{A_{\rm T}}{2} \cdot \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot \delta (f \pm (f_{\rm T}+ n \cdot f_{\rm N}))\hspace{0.05cm}.$$
(6) Under the suggested conditions, all the Bessel lines ${\rm J}_{|n|>3}$ can be disregarded.
- This gives $B_{\rm K} = 2 · 3 · f_{\rm N}\hspace{0.15cm}\underline { = 18 \ \rm kHz}$.
(7) The numerical values in the table given on the exercise page show that the following channel bandwidths would now be required:
- für $η = 2$: $B_{\rm K} \hspace{0.15cm}\underline { = 24 \ \rm kHz}$,
- für $η = 3$: $B_{\rm K} \hspace{0.15cm}\underline { = 36 \ \rm kHz}$.