Difference between revisions of "Aufgaben:Exercise 4.10: Signal Waveforms of the 16-QAM"
m |
|||
| (4 intermediate revisions by 2 users not shown) | |||
| Line 7: | Line 7: | ||
Let us consider the 16–QAM method according to the [[Modulation_Methods/Quadrature_Amplitude_Modulation#General_description_and_signal_space_allocation|block diagram]] in the theory section. | Let us consider the 16–QAM method according to the [[Modulation_Methods/Quadrature_Amplitude_Modulation#General_description_and_signal_space_allocation|block diagram]] in the theory section. | ||
| − | Very briefly, it can be described as follows: | + | Very briefly, it can be described as follows: |
| − | *After serial-parallel conversion and subsequent signal space assignment, four bits of the binary redundancy-free source signal $q(t)$ at the input each result in a complex-valued amplitude coefficient | + | *After serial-parallel conversion and subsequent signal space assignment, four bits of the binary redundancy-free source signal $q(t)$ at the input each result in a complex-valued amplitude coefficient |
:$$a = a_{\rm I} +{\rm j} · a_{\rm Q}.$$ | :$$a = a_{\rm I} +{\rm j} · a_{\rm Q}.$$ | ||
| − | *With the | + | *With the rectangular transmission pulse $g_s(t)$ in the range from $0$ to $T$ and of height $g_0$, after multiplication with the cosine function or minus-sine function in the given time interval, we obtain: |
:$$s_{\rm cos}(t) = a_{\rm I}\cdot g_0 \cdot \cos(2 \pi f_{\rm T} t)\hspace{0.05cm},$$ | :$$s_{\rm cos}(t) = a_{\rm I}\cdot g_0 \cdot \cos(2 \pi f_{\rm T} t)\hspace{0.05cm},$$ | ||
:$$ s_{\rm -sin}(t) = -a_{\rm Q} \cdot g_0 \cdot \sin(2 \pi f_{\rm T} t)\hspace{0.05cm}.$$ | :$$ s_{\rm -sin}(t) = -a_{\rm Q} \cdot g_0 \cdot \sin(2 \pi f_{\rm T} t)\hspace{0.05cm}.$$ | ||
| − | * The 16-QAM | + | * The 16-QAM transmitted signal is then the sum of these two component signals: |
:$$s(t) = s_{\rm cos}(t)+ s_{\rm -sin}(t) \hspace{0.05cm}.$$ | :$$s(t) = s_{\rm cos}(t)+ s_{\rm -sin}(t) \hspace{0.05cm}.$$ | ||
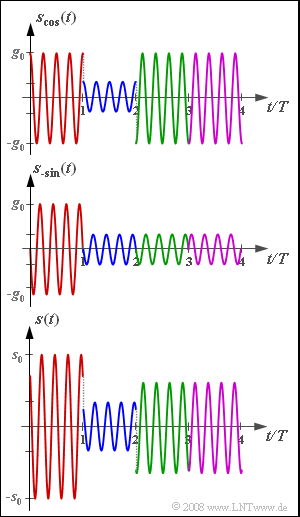
| − | The graph shows the signals $s_{\rm cos}(t)$, $s_{\rm –sin}(t)$ and $s(t)$ for four selected symbols. Using these, the amplitude coefficients are to be determined. | + | The graph shows the signals $s_{\rm cos}(t)$, $s_{\rm –sin}(t)$ and $s(t)$ for four selected symbols. Using these, the amplitude coefficients are to be determined. |
| − | + | Hints: | |
| − | + | *This exercise belongs to the chapter [[Modulation_Methods/Quadrature_Amplitude_Modulation|"Quadrature Amplitude Modulation"]]. | |
| − | + | *The page [[Modulation_Methods/Quadrature_Amplitude_Modulation#Signal_waveforms_for_4.E2.80.93QAM|"Signal waveforms for 4–QAM"]] is helpful for completing this exercise. | |
| − | + | *The signal space allocation considered can be seen in [[Aufgaben:Exercise_4.10Z:_Signal_Space_Constellation_of_the_16-QAM|Exercise 4.10Z]]. The color highlights also correspond. | |
| − | + | *From question '''(6)''' onwards, use the parameter values $g_0 = 1 \ \rm V$ and $T = 1 \ \rm µ s$. | |
| − | *This exercise belongs to the chapter [[Modulation_Methods/Quadrature_Amplitude_Modulation|Quadrature Amplitude Modulation]]. | + | *Energy values are to be given in $\rm V^2s$ ; like this, they refer to the reference resistance $R = 1 \ \rm \Omega$. |
| − | *The page [[Modulation_Methods/Quadrature_Amplitude_Modulation#Signal_waveforms_for_4.E2.80.93QAM|Signal waveforms for 4–QAM]] is helpful for completing this exercise. | ||
| − | *The signal space allocation considered can be seen in | ||
| − | |||
| − | *From question '''(6)''' onwards, use the parameter values $g_0 = 1 \ \rm V$ and $T = 1 \ \rm µ s$. | ||
| − | *Energy values are to be given in $\rm V^2s$ ; like this, they refer to the reference resistance | ||
| − | $R = 1 \ \rm \Omega$. | ||
| Line 39: | Line 33: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {What are the real and imaginary | + | {What are the real and imaginary part of the amplitude coefficient $a$ in the red time interval $(0 < t < T)$? |
|type="{}"} | |type="{}"} | ||
$a_{\rm I} \ = \ $ { 1 3% } | $a_{\rm I} \ = \ $ { 1 3% } | ||
| Line 45: | Line 39: | ||
| − | {What is the relationship between $s_0$ (maximum envelope of the transmitted signal) and $g_0$ (maximum envelope of the partial signals)? | + | {What is the relationship between $s_0$ (maximum envelope of the transmitted signal) and $g_0$ (maximum envelope of the partial signals)? |
|type="{}"} | |type="{}"} | ||
$s_0/g_0 \ = \ $ { 1.414 3% } | $s_0/g_0 \ = \ $ { 1.414 3% } | ||
| Line 54: | Line 48: | ||
$a_{\rm Q} \ = \ $ { 0.333 3% } | $a_{\rm Q} \ = \ $ { 0.333 3% } | ||
| − | {What is the amplitude coefficient $a$ in the green time interval $(2T < t < 3T)$? | + | {What is the amplitude coefficient $a$ in the green time interval $(2T < t < 3T)$? Determine also its magnitude and phase. |
|type="{}"} | |type="{}"} | ||
$a_{\rm I} \ = \ $ { -1.03--0.97 } | $a_{\rm I} \ = \ $ { -1.03--0.97 } | ||
| Line 80: | Line 74: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' From the (red) inphase signal ⇒ the real part follows (first equation according to the definition, second equation according to the graph): | + | '''(1)''' From the (red) inphase signal ⇒ the real part follows (first equation according to the definition, second equation according to the graph): |
:$$ s_{\rm cos}(t)= a_{\rm I}\cdot g_0 \cdot \cos(2 \pi f_{\rm T} t)= g_0 \cdot \cos(2 \pi f_{\rm T} t)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}a_{\rm I}\hspace{0.15cm}\underline {= +1} \hspace{0.05cm}.$$ | :$$ s_{\rm cos}(t)= a_{\rm I}\cdot g_0 \cdot \cos(2 \pi f_{\rm T} t)= g_0 \cdot \cos(2 \pi f_{\rm T} t)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}a_{\rm I}\hspace{0.15cm}\underline {= +1} \hspace{0.05cm}.$$ | ||
| − | *Accordingly, we recognize from the quadrature signal ⇒ imaginary part: | + | *Accordingly, we recognize from the quadrature signal ⇒ imaginary part: |
:$$ s_{\rm -sin}(t)= -a_{\rm Q}\cdot g_0 \cdot \sin(2 \pi f_{\rm T} t)= -g_0 \cdot \sin(2 \pi f_{\rm T} t)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}a_{\rm Q}\hspace{0.15cm}\underline {= +1} \hspace{0.05cm}.$$ | :$$ s_{\rm -sin}(t)= -a_{\rm Q}\cdot g_0 \cdot \sin(2 \pi f_{\rm T} t)= -g_0 \cdot \sin(2 \pi f_{\rm T} t)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}a_{\rm Q}\hspace{0.15cm}\underline {= +1} \hspace{0.05cm}.$$ | ||
| − | '''(2)''' The two partial signals each have the (maximum) envelope $g_0$, while $s_0$ characterizes the transmitted signal $s(t)$ | + | '''(2)''' The two partial signals each have the (maximum) envelope $g_0$, while $s_0$ characterizes the transmitted signal $s(t)$. |
*As can be seen from the signal space allocation (see Exercise 4.10Z) : | *As can be seen from the signal space allocation (see Exercise 4.10Z) : | ||
:$${s_0}/{ g_0 }= \sqrt{2}\hspace{0.15cm}\underline { = 1.414} \hspace{0.05cm}.$$ | :$${s_0}/{ g_0 }= \sqrt{2}\hspace{0.15cm}\underline { = 1.414} \hspace{0.05cm}.$$ | ||
| Line 93: | Line 87: | ||
| − | '''(3)''' The amplitude coefficients $a_{\rm I}$ and $a_{\rm Q}$ have the same signs as in subtask '''(1)''', but with smaller magnitude: | + | '''(3)''' The amplitude coefficients $a_{\rm I}$ and $a_{\rm Q}$ have the same signs as in subtask '''(1)''', but with smaller magnitude: |
:$$a_{\rm I} = + 1/3\hspace{0.15cm}\underline {= +0.333} \hspace{0.05cm},\hspace{0.5cm}a_{\rm Q} = + 1/3\hspace{0.15cm}\underline {= +0.333} \hspace{0.05cm}.$$ | :$$a_{\rm I} = + 1/3\hspace{0.15cm}\underline {= +0.333} \hspace{0.05cm},\hspace{0.5cm}a_{\rm Q} = + 1/3\hspace{0.15cm}\underline {= +0.333} \hspace{0.05cm}.$$ | ||
| − | '''(4)''' In the third (green) interval, we can see a minus cosine signal with amplitude $g_0$ and a minus sine signal with amplitude $g_0/3$: | + | '''(4)''' In the third (green) interval, we can see a minus-cosine signal with amplitude $g_0$ and a minus-sine signal with amplitude $g_0/3$: |
:$$a_{\rm I} = \hspace{0.15cm}\underline {= -1} \hspace{0.05cm},\hspace{0.5cm}a_{\rm Q} = + 1/3\hspace{0.15cm}\underline {= +0.333} \hspace{0.05cm}.$$ | :$$a_{\rm I} = \hspace{0.15cm}\underline {= -1} \hspace{0.05cm},\hspace{0.5cm}a_{\rm Q} = + 1/3\hspace{0.15cm}\underline {= +0.333} \hspace{0.05cm}.$$ | ||
| − | As is yet to be calculated in sub-task '''(4)''' of Exercise 4.10Z, here the magnitude is equal to $|a| =1.054$ and the phase angle is ${\rm arc} \ a \approx 161^\circ$. | + | *As is yet to be calculated in sub-task '''(4)''' of Exercise 4.10Z, here the magnitude is equal to $|a| =1.054$ and the phase angle is ${\rm arc} \ a \approx 161^\circ$. |
| Line 111: | Line 105: | ||
'''(6)''' The maximum signal energy occurs when one of the four outer vertices is occupied. In that case: | '''(6)''' The maximum signal energy occurs when one of the four outer vertices is occupied. In that case: | ||
:$$ E_{\rm S, \hspace{0.05cm}max} = {1}/{2}\cdot s_0^2 \cdot T = {1}/{2}\cdot \left (\sqrt{2} \cdot g_0 \right )^2 \cdot T = g_0^2 \cdot T = (1\,{\rm V})^2 \cdot (1\,{\rm \mu s}) \hspace{0.15cm}\underline {= 10^{-6}\,{\rm V^2s}}\hspace{0.05cm}.$$ | :$$ E_{\rm S, \hspace{0.05cm}max} = {1}/{2}\cdot s_0^2 \cdot T = {1}/{2}\cdot \left (\sqrt{2} \cdot g_0 \right )^2 \cdot T = g_0^2 \cdot T = (1\,{\rm V})^2 \cdot (1\,{\rm \mu s}) \hspace{0.15cm}\underline {= 10^{-6}\,{\rm V^2s}}\hspace{0.05cm}.$$ | ||
| − | *The average signal energy is equal to the maximum value when only the corner points of the signal space mapping are occupied and the "inner symbols" are excluded from the encoding. | + | *The average signal energy is equal to the maximum value when only the corner points of the signal space mapping are occupied and the "inner symbols" are excluded from the encoding. |
| − | '''(7)''' Four bits are transmitted per symbol. From this it follows that: | + | '''(7)''' Four bits are transmitted per symbol. From this it follows that: |
:$$ E_{\rm B, \hspace{0.05cm}max} = {E_{\rm S, \hspace{0.05cm}max}}/{4}\hspace{0.15cm}\underline {= 0.25 \cdot 10^{-6}\,{\rm V^2s}}\hspace{0.05cm}.$$ | :$$ E_{\rm B, \hspace{0.05cm}max} = {E_{\rm S, \hspace{0.05cm}max}}/{4}\hspace{0.15cm}\underline {= 0.25 \cdot 10^{-6}\,{\rm V^2s}}\hspace{0.05cm}.$$ | ||
| − | '''(8)''' The minimum signal energy is obtained at one of the inner signal space points and is smaller by a factor of $9$ than in subtask '''(7)''': | + | '''(8)''' The minimum signal energy is obtained at one of the inner signal space points and is smaller by a factor of $9$ than in subtask '''(7)''': |
:$$E_{\rm B, \hspace{0.05cm}min} = \frac{E_{\rm B, \hspace{0.05cm}max}}{9} = \frac{g_0^2 \cdot T}{36} \hspace{0.15cm}\underline { \approx 0.028 \cdot 10^{-6}\,{\rm V^2s}}\hspace{0.05cm}.$$ | :$$E_{\rm B, \hspace{0.05cm}min} = \frac{E_{\rm B, \hspace{0.05cm}max}}{9} = \frac{g_0^2 \cdot T}{36} \hspace{0.15cm}\underline { \approx 0.028 \cdot 10^{-6}\,{\rm V^2s}}\hspace{0.05cm}.$$ | ||
| − | *In the theory section, it was shown that, assuming all symbols are equally likely, the average signal energy per bit for 16-QAM is approximately: | + | *In the theory section, it was shown that, assuming all symbols are equally likely, the average signal energy per bit for 16-QAM is approximately: |
:$$E_{\rm B} \approx 0.139 · g_0^2 \cdot T = 0.035 \cdot 10^{-6}\,{\rm V^2s}.$$ | :$$E_{\rm B} \approx 0.139 · g_0^2 \cdot T = 0.035 \cdot 10^{-6}\,{\rm V^2s}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 16:20, 23 January 2023
Let us consider the 16–QAM method according to the block diagram in the theory section.
Very briefly, it can be described as follows:
- After serial-parallel conversion and subsequent signal space assignment, four bits of the binary redundancy-free source signal $q(t)$ at the input each result in a complex-valued amplitude coefficient
- $$a = a_{\rm I} +{\rm j} · a_{\rm Q}.$$
- With the rectangular transmission pulse $g_s(t)$ in the range from $0$ to $T$ and of height $g_0$, after multiplication with the cosine function or minus-sine function in the given time interval, we obtain:
- $$s_{\rm cos}(t) = a_{\rm I}\cdot g_0 \cdot \cos(2 \pi f_{\rm T} t)\hspace{0.05cm},$$
- $$ s_{\rm -sin}(t) = -a_{\rm Q} \cdot g_0 \cdot \sin(2 \pi f_{\rm T} t)\hspace{0.05cm}.$$
- The 16-QAM transmitted signal is then the sum of these two component signals:
- $$s(t) = s_{\rm cos}(t)+ s_{\rm -sin}(t) \hspace{0.05cm}.$$
The graph shows the signals $s_{\rm cos}(t)$, $s_{\rm –sin}(t)$ and $s(t)$ for four selected symbols. Using these, the amplitude coefficients are to be determined.
Hints:
- This exercise belongs to the chapter "Quadrature Amplitude Modulation".
- The page "Signal waveforms for 4–QAM" is helpful for completing this exercise.
- The signal space allocation considered can be seen in Exercise 4.10Z. The color highlights also correspond.
- From question (6) onwards, use the parameter values $g_0 = 1 \ \rm V$ and $T = 1 \ \rm µ s$.
- Energy values are to be given in $\rm V^2s$ ; like this, they refer to the reference resistance $R = 1 \ \rm \Omega$.
Questions
Solution
- $$ s_{\rm cos}(t)= a_{\rm I}\cdot g_0 \cdot \cos(2 \pi f_{\rm T} t)= g_0 \cdot \cos(2 \pi f_{\rm T} t)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}a_{\rm I}\hspace{0.15cm}\underline {= +1} \hspace{0.05cm}.$$
- Accordingly, we recognize from the quadrature signal ⇒ imaginary part:
- $$ s_{\rm -sin}(t)= -a_{\rm Q}\cdot g_0 \cdot \sin(2 \pi f_{\rm T} t)= -g_0 \cdot \sin(2 \pi f_{\rm T} t)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}a_{\rm Q}\hspace{0.15cm}\underline {= +1} \hspace{0.05cm}.$$
(2) The two partial signals each have the (maximum) envelope $g_0$, while $s_0$ characterizes the transmitted signal $s(t)$.
- As can be seen from the signal space allocation (see Exercise 4.10Z) :
- $${s_0}/{ g_0 }= \sqrt{2}\hspace{0.15cm}\underline { = 1.414} \hspace{0.05cm}.$$
(3) The amplitude coefficients $a_{\rm I}$ and $a_{\rm Q}$ have the same signs as in subtask (1), but with smaller magnitude:
- $$a_{\rm I} = + 1/3\hspace{0.15cm}\underline {= +0.333} \hspace{0.05cm},\hspace{0.5cm}a_{\rm Q} = + 1/3\hspace{0.15cm}\underline {= +0.333} \hspace{0.05cm}.$$
(4) In the third (green) interval, we can see a minus-cosine signal with amplitude $g_0$ and a minus-sine signal with amplitude $g_0/3$:
- $$a_{\rm I} = \hspace{0.15cm}\underline {= -1} \hspace{0.05cm},\hspace{0.5cm}a_{\rm Q} = + 1/3\hspace{0.15cm}\underline {= +0.333} \hspace{0.05cm}.$$
- As is yet to be calculated in sub-task (4) of Exercise 4.10Z, here the magnitude is equal to $|a| =1.054$ and the phase angle is ${\rm arc} \ a \approx 161^\circ$.
(5) The violet signal does not differ from the green interval in the in-phase component except in the sign of the quadrature component:
- $$a_{\rm I} = \hspace{0.15cm}\underline {= -1} \hspace{0.05cm},\hspace{0.5cm}a_{\rm Q} = - 1/3\hspace{0.15cm}\underline {= -0.333} \hspace{0.05cm}.$$
(6) The maximum signal energy occurs when one of the four outer vertices is occupied. In that case:
- $$ E_{\rm S, \hspace{0.05cm}max} = {1}/{2}\cdot s_0^2 \cdot T = {1}/{2}\cdot \left (\sqrt{2} \cdot g_0 \right )^2 \cdot T = g_0^2 \cdot T = (1\,{\rm V})^2 \cdot (1\,{\rm \mu s}) \hspace{0.15cm}\underline {= 10^{-6}\,{\rm V^2s}}\hspace{0.05cm}.$$
- The average signal energy is equal to the maximum value when only the corner points of the signal space mapping are occupied and the "inner symbols" are excluded from the encoding.
(7) Four bits are transmitted per symbol. From this it follows that:
- $$ E_{\rm B, \hspace{0.05cm}max} = {E_{\rm S, \hspace{0.05cm}max}}/{4}\hspace{0.15cm}\underline {= 0.25 \cdot 10^{-6}\,{\rm V^2s}}\hspace{0.05cm}.$$
(8) The minimum signal energy is obtained at one of the inner signal space points and is smaller by a factor of $9$ than in subtask (7):
- $$E_{\rm B, \hspace{0.05cm}min} = \frac{E_{\rm B, \hspace{0.05cm}max}}{9} = \frac{g_0^2 \cdot T}{36} \hspace{0.15cm}\underline { \approx 0.028 \cdot 10^{-6}\,{\rm V^2s}}\hspace{0.05cm}.$$
- In the theory section, it was shown that, assuming all symbols are equally likely, the average signal energy per bit for 16-QAM is approximately:
- $$E_{\rm B} \approx 0.139 · g_0^2 \cdot T = 0.035 \cdot 10^{-6}\,{\rm V^2s}.$$