Difference between revisions of "Aufgaben:Exercise 3.4: Optimization of the Cutoff Frequency"
| (12 intermediate revisions by 2 users not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File: | + | [[File:EN_Dig_A_3_4.png|right|frame|System sizes for binary and quaternary systems and for different cutoff frequencies]] |
We compare a redundancy-free binary system $(M = 2)$ and a redundancy-free quaternary system $(M = 4)$ in terms of their worst-case S/N ratios: | We compare a redundancy-free binary system $(M = 2)$ and a redundancy-free quaternary system $(M = 4)$ in terms of their worst-case S/N ratios: | ||
:$$\rho_{\rm U} = \frac{\big[\ddot{o}(T_{\rm D})/2 \big]^2}{ \sigma_d^2} \hspace{0.05cm}.$$ | :$$\rho_{\rm U} = \frac{\big[\ddot{o}(T_{\rm D})/2 \big]^2}{ \sigma_d^2} \hspace{0.05cm}.$$ | ||
| − | $\ddot{o}(T_{\rm D})$ is the vertical eye opening and $\sigma_d^2$ indicates the detection noise power. The same boundary conditions apply to both system configurations (similar to [[Aufgaben: | + | $\ddot{o}(T_{\rm D})$ is the vertical eye opening and $\sigma_d^2$ indicates the detection noise power. The same boundary conditions apply to both system configurations (similar to [[Aufgaben:Exercise_3.4Z:_Eye_Opening_and_Level_Number|Exercise 3.4Z]]): |
* The rectangular basic transmission pulse $g_s(t)$ in NRZ format has the height $s_0 = 1 \, {\rm V}$. | * The rectangular basic transmission pulse $g_s(t)$ in NRZ format has the height $s_0 = 1 \, {\rm V}$. | ||
| + | |||
* The (equivalent) bit rate is $R_{\rm B} = 100 \, {\rm Mbit/s}$ in both cases. | * The (equivalent) bit rate is $R_{\rm B} = 100 \, {\rm Mbit/s}$ in both cases. | ||
| − | * The channel consists of a coaxial cable with the characteristic cable attenuation $a_* = 80 \, {\rm dB} | + | |
| − | * Let the receiver filter be a Gaussian low-pass filter with cutoff frequency $f_{\rm G}$, which is to be optimized: | + | * The channel consists of a coaxial cable with the characteristic cable attenuation $a_* = 80 \, {\rm dB}\Rightarrow 9.2 \, {\rm Np}$. |
| + | |||
| + | * Let the receiver filter be a Gaussian low-pass filter with cutoff frequency $f_{\rm G}$, which is to be optimized: | ||
:$$H_{\rm G}(f) = {\rm e}^{{- \pi \cdot f^2}/{(2f_{\rm G})^2}}\hspace{0.05cm}.$$ | :$$H_{\rm G}(f) = {\rm e}^{{- \pi \cdot f^2}/{(2f_{\rm G})^2}}\hspace{0.05cm}.$$ | ||
| − | * AWGN noise with | + | * AWGN noise with (one-sided) power-spectral density $N_0$ is present at the channel output. |
| + | |||
* The decision thresholds are optimally selected and the detection time $T_{\rm D} = 0$ is also best possible. | * The decision thresholds are optimally selected and the detection time $T_{\rm D} = 0$ is also best possible. | ||
| − | In contrast to [[Aufgaben: | + | In contrast to [[Aufgaben:Exercise_3.4Z:_Eye_Opening_and_Level_Number|Exercise 3.4Z]] $($fixed cutoff frequency $f_{\rm G} = 30 \, {\rm MHz}),$ the cutoff frequency of the low-pass filter is variable here. This is to be determined in such a way that the worst-case S/N ratio $\rho_{\rm U}$ is maximized and thus the worst-case error probability $p_{\rm U}$ is minimized. |
The table shows | The table shows | ||
| − | *the (normalized) half eye opening and | + | *the (normalized) half eye opening, and |
| − | *the (normalized) detection noise rms value | + | *the (normalized) detection noise rms value |
| − | for the binary system $(M = 2)$ and the quaternary system $(M = 4)$ as well as for different (normalized) cutoff frequencies. The normalization is based on the bit rate $R_{\rm B}$. | + | for the binary system $(M = 2)$ and the quaternary system $(M = 4)$ as well as for different (normalized) cutoff frequencies. The normalization is based on the bit rate $R_{\rm B}$. |
To be noted: | To be noted: | ||
| − | * The table is valid for $E_{\rm B}/N_0 = 5 \cdot 10^8$ and $a_* = 80 \, {\rm dB} | + | * The table is valid for $E_{\rm B}/N_0 = 5 \cdot 10^8$ and $a_* = 80 \, {\rm dB}\Rightarrow 9.2 \, {\rm Np}$. |
| − | * | + | |
| + | * Taking into account the ideal channel equalizer, the normalized noise power results in | ||
:$$\frac{ \sigma_d^2}{N_{\rm 0} \cdot R_{\rm B}} = \frac{ 1}{R_{\rm | :$$\frac{ \sigma_d^2}{N_{\rm 0} \cdot R_{\rm B}} = \frac{ 1}{R_{\rm | ||
B}} \cdot \int_{0}^{\infty}{\rm exp}\left [2 \cdot 9.2 | B}} \cdot \int_{0}^{\infty}{\rm exp}\left [2 \cdot 9.2 | ||
| Line 34: | Line 39: | ||
B})^2}{(2 f_{\rm G}/R_{\rm B})^2} \right ]{\rm d} \hspace{0.05cm} f | B})^2}{(2 f_{\rm G}/R_{\rm B})^2} \right ]{\rm d} \hspace{0.05cm} f | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * As will be derived in [[Aufgaben: | + | * As will be derived in [[Aufgaben:Exercise_3.4Z:_Eye_Opening_and_Level_Number|Exercise 3.4Z]], the following holds for the (normalized) half eye opening: |
:$$\frac{\ddot{o}(T_{\rm D})}{ 2 \cdot s_0} = \frac{1}{ M-1}\cdot \big [1- 2 \cdot M \cdot {\rm Q} \left( | :$$\frac{\ddot{o}(T_{\rm D})}{ 2 \cdot s_0} = \frac{1}{ M-1}\cdot \big [1- 2 \cdot M \cdot {\rm Q} \left( | ||
\sqrt{2\pi} \cdot {\rm log_2}\hspace{0.1cm}(M) \cdot {f_{\rm | \sqrt{2\pi} \cdot {\rm log_2}\hspace{0.1cm}(M) \cdot {f_{\rm | ||
| Line 40: | Line 45: | ||
\right)\big] | \right)\big] | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * Thus, for the worst case S/N ratio, the last term can be interpreted as " | + | * Thus, for the worst case S/N ratio, the last term can be interpreted as "energy per bit related to noise power density" for the NRZ rectangular pulse considered here: |
:$$\rho_{\rm U} = \left [\frac{\ddot{o}(T_{\rm D})}{ 2 \cdot s_0} \right ]^2 \cdot | :$$\rho_{\rm U} = \left [\frac{\ddot{o}(T_{\rm D})}{ 2 \cdot s_0} \right ]^2 \cdot | ||
\frac{N_{\rm 0} \cdot R_{\rm B}}{ \sigma_d^2} \cdot \frac{ s_0^2}{N_{\rm 0} \cdot R_{\rm B}} | \frac{N_{\rm 0} \cdot R_{\rm B}}{ \sigma_d^2} \cdot \frac{ s_0^2}{N_{\rm 0} \cdot R_{\rm B}} | ||
| Line 48: | Line 53: | ||
| + | Notes: | ||
| + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/Intersymbol_Interference_for_Multi-Level_Transmission|"Intersymbol Interference for Multi-Level Transmission"]]. | ||
| + | *In the table, $\sigma_d/s_0$ is given, which means that the second and third terms of the above equation are combined here. | ||
| − | + | *By dividing the first column element ("normalized half eye opening") by the second element $(\sigma_d/s_0)$ and squaring the quotient, the result $\rho_{\rm U}$ is obtained very easily. | |
| − | |||
| − | |||
| − | *By dividing the first column element (normalized half eye opening) by the second element $(\sigma_d/s_0)$ | ||
| Line 64: | Line 69: | ||
$M = 4, f_{\rm G} = 0.28\text{:}\hspace{0.4cm} \sigma_d/s_0 \ = \ $ { 0.021 3% } | $M = 4, f_{\rm G} = 0.28\text{:}\hspace{0.4cm} \sigma_d/s_0 \ = \ $ { 0.021 3% } | ||
| − | {Determine the optimal cutoff frequency and achievable | + | {Determine the optimal cutoff frequency and the achievable worst-case signal-to-noise ratio for the binary system. |
|type="{}"} | |type="{}"} | ||
$M = 2\text{:}\hspace{0.9cm} f_{\rm G, \ opt}/R_{\rm B}\ = \ $ { 0.33 3% } | $M = 2\text{:}\hspace{0.9cm} f_{\rm G, \ opt}/R_{\rm B}\ = \ $ { 0.33 3% } | ||
$M = 2\text{:}\hspace{0.4cm} 10 \cdot {\rm lg} \, \rho_{\rm U, \ max}\ = \ $ { 11.85 3% } ${\ \rm dB}$ | $M = 2\text{:}\hspace{0.4cm} 10 \cdot {\rm lg} \, \rho_{\rm U, \ max}\ = \ $ { 11.85 3% } ${\ \rm dB}$ | ||
| − | {Find the optimal cutoff frequency and achievable | + | {Find the optimal cutoff frequency and the achievable worst-case signal-to-noise ratio for the quaternary system. |
|type="{}"} | |type="{}"} | ||
$M = 4\text{:}\hspace{0.97cm} f_{\rm G, \ opt}/R_{\rm B}\ = \ ${ 0.28 3% } | $M = 4\text{:}\hspace{0.97cm} f_{\rm G, \ opt}/R_{\rm B}\ = \ ${ 0.28 3% } | ||
$M = 4\text{:}\hspace{0.4cm} 10 \cdot {\rm lg} \, \rho_{\rm U,\ max}\ = \ $ { 15.21 3% } ${\ \rm dB}$ | $M = 4\text{:}\hspace{0.4cm} 10 \cdot {\rm lg} \, \rho_{\rm U,\ max}\ = \ $ { 15.21 3% } ${\ \rm dB}$ | ||
| − | {Evaluate the results of subtasks '''(2)''' and '''(3)''' using the following statements. Which of them are true? | + | {Evaluate the results of subtasks '''(2)''' and '''(3)''' using the following statements. Which of them are true? |
|type="[]"} | |type="[]"} | ||
| − | + If the normalized cutoff frequency $f_{\rm G}/R_{\rm B} ≥ 0.35$, the binary system is superior to the quaternary system. | + | + If the normalized cutoff frequency $f_{\rm G}/R_{\rm B} ≥ 0.35$, the binary system is superior to the quaternary system. |
- If the normalized cutoff frequency $f_{\rm G}/R_{\rm B} = 0.33$, the binary system is superior to the quaternary system. | - If the normalized cutoff frequency $f_{\rm G}/R_{\rm B} = 0.33$, the binary system is superior to the quaternary system. | ||
| − | + The main reason for the superiority of the quaternary system over the binary system (optimized in each case) is the lower symbol rate. | + | + The main reason for the superiority of the quaternary system over the binary system (optimized in each case) is the lower symbol rate. |
| − | + From the present values, it can be concluded that the (optimal) quaternary system is also better for $a_* = 100 \, {\rm dB}$. | + | + From the present values, it can be concluded that the (optimal) quaternary system is also better for $a_* = 100 \, {\rm dB}$. |
| − | - From the present values, it can be concluded that the (optimal) quaternary system is also better for $a_* = 40 \, {\rm dB}$. | + | - From the present values, it can be concluded that the (optimal) quaternary system is also better for $a_* = 40 \, {\rm dB}$. |
</quiz> | </quiz> | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Normalizing the cutoff frequency $f_{\rm G}$ to the bit rate $R_{\rm B}$ (and not to the symbol rate $1/T$ | + | '''(1)''' Normalizing the cutoff frequency $f_{\rm G}$ to the bit rate $R_{\rm B}$ $($and not to the symbol rate $1/T)$, the given noise rms values hold independently of the level number. Thus one obtains: |
:$$M = 2, \hspace{0.1cm}f_{\rm G}/R_{\rm B} = 0.33\text{:} \hspace{0.2cm} | :$$M = 2, \hspace{0.1cm}f_{\rm G}/R_{\rm B} = 0.33\text{:} \hspace{0.2cm} | ||
\sigma_d/s_0 \ \hspace{0.15cm}\underline { = 0.047} | \sigma_d/s_0 \ \hspace{0.15cm}\underline { = 0.047} | ||
| Line 93: | Line 98: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | '''(2)''' The optimum cutoff frequency is given when the quotient of (half) eye opening and noise rms value is maximum. | + | '''(2)''' The optimum cutoff frequency is given when the quotient of the (half) eye opening and the noise rms value is maximum. |
| − | *The optimum results for the binary system for $f_{\rm G}/R_{\rm B} \underline {= 0.33}$: | + | *The optimum results for the binary system for $f_{\rm G}/R_{\rm B} \underline {= 0.33}$: |
:$$\rho_{\rm U,\hspace{0.05cm} max} = \frac{0.184^2}{ 0.047^2} = 15.32 | :$$\rho_{\rm U,\hspace{0.05cm} max} = \frac{0.184^2}{ 0.047^2} = 15.32 | ||
\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| Line 101: | Line 106: | ||
dB}} \hspace{0.05cm}.$$ | dB}} \hspace{0.05cm}.$$ | ||
| − | *In contrast, for the adjacent cutoff frequency values: | + | *In contrast, for the adjacent cutoff frequency values: |
:$$f_{\rm G}/R_{\rm B} = 0.32\text{:} \hspace{0.2cm}\rho_{\rm U} = \frac{0.155^2}{ 0.040^2} = 15.02 | :$$f_{\rm G}/R_{\rm B} = 0.32\text{:} \hspace{0.2cm}\rho_{\rm U} = \frac{0.155^2}{ 0.040^2} = 15.02 | ||
\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| Line 111: | Line 116: | ||
10 \cdot {\rm | 10 \cdot {\rm | ||
lg}\hspace{0.1cm}\rho_{\rm U} = 11.72\,{\rm dB} \hspace{0.05cm}.$$ | lg}\hspace{0.1cm}\rho_{\rm U} = 11.72\,{\rm dB} \hspace{0.05cm}.$$ | ||
| − | *From this, one can see the optimum, albeit a flat one. | + | *From this, one can see the optimum, albeit a flat one. |
| Line 128: | Line 133: | ||
lg}\hspace{0.1cm}\rho_{\rm U} = 14.90\,{\rm dB} \hspace{0.05cm}.$$ | lg}\hspace{0.1cm}\rho_{\rm U} = 14.90\,{\rm dB} \hspace{0.05cm}.$$ | ||
| − | *Thus, the optimum cutoff frequency is $f_{\rm G}/R_{\rm B} \underline {= 0.28}$ for the quaternary system. | + | *Thus, the optimum cutoff frequency is $f_{\rm G}/R_{\rm B} \underline {= 0.28}$ for the quaternary system. |
| − | *The signal-to-noise ratio is then more than $3 \, {\rm dB}$ larger than for the binary system with optimized cutoff frequency. | + | *The signal-to-noise ratio is then more than $3 \, {\rm dB}$ larger than for the binary system with optimized cutoff frequency. |
| − | '''(4)''' <u>Statements 1, 3 and 4</u> are correct: | + | '''(4)''' <u>Statements 1, 3 and 4</u> are correct: |
| − | *The correctness of the first statement is confirmed by the table. For $f_{\rm G}/R_{\rm B} ≥ 0.35$, the binary system has a larger eye opening than the quaternary system. Moreover, by normalizing all frequencies to the bit rate, the noise rms value is independent of the number | + | *The correctness of the first statement is confirmed by the table. For $f_{\rm G}/R_{\rm B} ≥ 0.35$, the binary system has a larger eye opening than the quaternary system. Moreover, by normalizing all frequencies to the bit rate, the noise rms value is independent of the level number $M$, so that the optimization can be restricted to the eye opening. |
| − | *For $f_{\rm G}/R_{\rm B} < 0.35$, on the other hand, the quaternary system is better, so also for $f_{\rm G}/R_{\rm B} = 0.33$. Although this cutoff frequency is optimal for $M = 2$ and not for $M = 4$, with $f_{\rm G}/R_{\rm B} = 0.33$ the quaternary system is better than the binary system by about $0.85 \, {\rm dB}$. | + | *For $f_{\rm G}/R_{\rm B} < 0.35$, on the other hand, the quaternary system is better, so also for $f_{\rm G}/R_{\rm B} = 0.33$. Although this cutoff frequency is optimal for $M = 2$ and not for $M = 4$, with $f_{\rm G}/R_{\rm B} = 0.33$ the quaternary system is better than the binary system by about $0.85 \, {\rm dB}$. |
| − | *The third statement is true. Due to the lower (more precisely: half) symbol rate, for $M = 4$ the eye is still open even with $f_{\rm G}/R_{\rm B} = 0.23$, while for a binary system there is already an (almost) closed eye for $f_{\rm G}/R_{\rm B} = 0.27$. | + | *The third statement is true. Due to the lower (more precisely: half) symbol rate, for $M = 4$ the eye is still open even with $f_{\rm G}/R_{\rm B} = 0.23$, while for a binary system there is already an (almost) closed eye for $f_{\rm G}/R_{\rm B} = 0.27$. |
| − | *With larger characteristic cable attenuation, the tendency goes to smaller and smaller cutoff frequency in order to keep the increase of the noise as small as possible. But if already at $a_* = 80 \, {\rm dB}$ the quaternary system (optimized with respect to cutoff frequency) is better, the same is true for $100 \, {\rm dB}$. The gain is larger than $15.21 | + | *With larger characteristic cable attenuation, the tendency goes to smaller and smaller cutoff frequency in order to keep the increase of the noise as small as possible. But if already at $a_* = 80 \, {\rm dB}$ the quaternary system (optimized with respect to cutoff frequency) is better, the same is true for $100 \, {\rm dB}$. The gain is larger than $15.21 - 11.85 \approx 3.4 \, {\rm dB}$. These values were obtained in questions '''(2)''' and '''(3)'''. |
| − | *In contrast, no statement is possible for the characteristic cable attenuation $a_* = 40 \, {\rm dB}$ based on the available numerical material. A system simulation provided the following results for this $($for $E_{\rm B}/N_0 = 50 \, {\rm dB})$: | + | *In contrast, no statement is possible for the characteristic cable attenuation $a_* = 40 \, {\rm dB}$ based on the available numerical material. A system simulation provided the following results for this $($for $E_{\rm B}/N_0 = 50 \, {\rm dB})$: |
| − | :$$M =2\text{:} \hspace{0.2cm}10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} = 15.43\,{\rm dB} \hspace{0.2cm}{\rm | + | :$$M =2\text{:} \hspace{0.2cm}10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} = 15.43\,{\rm dB} \hspace{0.2cm}{\rm with}\hspace{0.2cm} |
f_{\rm G}/R_{\rm B} \approx 0.4 \hspace{0.05cm},$$ | f_{\rm G}/R_{\rm B} \approx 0.4 \hspace{0.05cm},$$ | ||
| − | :$$M =4\text{:} \hspace{0.2cm}10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} = 14.65\,{\rm dB} \hspace{0.2cm}{\rm | + | :$$M =4\text{:} \hspace{0.2cm}10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} = 14.65\,{\rm dB} \hspace{0.2cm}{\rm with}\hspace{0.2cm} |
f_{\rm G}/R_{\rm B} \approx 0.32 \hspace{0.05cm}.$$ | f_{\rm G}/R_{\rm B} \approx 0.32 \hspace{0.05cm}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category:Digital Signal Transmission: Exercises|^3.4 | + | [[Category:Digital Signal Transmission: Exercises|^3.4 Eye Opening with Multilevel Systems^]] |
Latest revision as of 10:08, 27 June 2022
We compare a redundancy-free binary system $(M = 2)$ and a redundancy-free quaternary system $(M = 4)$ in terms of their worst-case S/N ratios:
- $$\rho_{\rm U} = \frac{\big[\ddot{o}(T_{\rm D})/2 \big]^2}{ \sigma_d^2} \hspace{0.05cm}.$$
$\ddot{o}(T_{\rm D})$ is the vertical eye opening and $\sigma_d^2$ indicates the detection noise power. The same boundary conditions apply to both system configurations (similar to Exercise 3.4Z):
- The rectangular basic transmission pulse $g_s(t)$ in NRZ format has the height $s_0 = 1 \, {\rm V}$.
- The (equivalent) bit rate is $R_{\rm B} = 100 \, {\rm Mbit/s}$ in both cases.
- The channel consists of a coaxial cable with the characteristic cable attenuation $a_* = 80 \, {\rm dB}\Rightarrow 9.2 \, {\rm Np}$.
- Let the receiver filter be a Gaussian low-pass filter with cutoff frequency $f_{\rm G}$, which is to be optimized:
- $$H_{\rm G}(f) = {\rm e}^{{- \pi \cdot f^2}/{(2f_{\rm G})^2}}\hspace{0.05cm}.$$
- AWGN noise with (one-sided) power-spectral density $N_0$ is present at the channel output.
- The decision thresholds are optimally selected and the detection time $T_{\rm D} = 0$ is also best possible.
In contrast to Exercise 3.4Z $($fixed cutoff frequency $f_{\rm G} = 30 \, {\rm MHz}),$ the cutoff frequency of the low-pass filter is variable here. This is to be determined in such a way that the worst-case S/N ratio $\rho_{\rm U}$ is maximized and thus the worst-case error probability $p_{\rm U}$ is minimized.
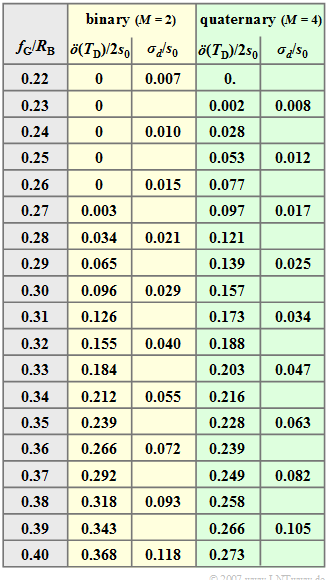
The table shows
- the (normalized) half eye opening, and
- the (normalized) detection noise rms value
for the binary system $(M = 2)$ and the quaternary system $(M = 4)$ as well as for different (normalized) cutoff frequencies. The normalization is based on the bit rate $R_{\rm B}$.
To be noted:
- The table is valid for $E_{\rm B}/N_0 = 5 \cdot 10^8$ and $a_* = 80 \, {\rm dB}\Rightarrow 9.2 \, {\rm Np}$.
- Taking into account the ideal channel equalizer, the normalized noise power results in
- $$\frac{ \sigma_d^2}{N_{\rm 0} \cdot R_{\rm B}} = \frac{ 1}{R_{\rm B}} \cdot \int_{0}^{\infty}{\rm exp}\left [2 \cdot 9.2 \cdot \sqrt{2 \cdot f/R_{\rm B}} - 2\pi \cdot \frac{(f/R_{\rm B})^2}{(2 f_{\rm G}/R_{\rm B})^2} \right ]{\rm d} \hspace{0.05cm} f \hspace{0.05cm}.$$
- As will be derived in Exercise 3.4Z, the following holds for the (normalized) half eye opening:
- $$\frac{\ddot{o}(T_{\rm D})}{ 2 \cdot s_0} = \frac{1}{ M-1}\cdot \big [1- 2 \cdot M \cdot {\rm Q} \left( \sqrt{2\pi} \cdot {\rm log_2}\hspace{0.1cm}(M) \cdot {f_{\rm G}}/{R_{\rm B}} \right)\big] \hspace{0.05cm}.$$
- Thus, for the worst case S/N ratio, the last term can be interpreted as "energy per bit related to noise power density" for the NRZ rectangular pulse considered here:
- $$\rho_{\rm U} = \left [\frac{\ddot{o}(T_{\rm D})}{ 2 \cdot s_0} \right ]^2 \cdot \frac{N_{\rm 0} \cdot R_{\rm B}}{ \sigma_d^2} \cdot \frac{ s_0^2}{N_{\rm 0} \cdot R_{\rm B}} \hspace{0.05cm}.$$
Notes:
- The exercise belongs to the chapter "Intersymbol Interference for Multi-Level Transmission".
- In the table, $\sigma_d/s_0$ is given, which means that the second and third terms of the above equation are combined here.
- By dividing the first column element ("normalized half eye opening") by the second element $(\sigma_d/s_0)$ and squaring the quotient, the result $\rho_{\rm U}$ is obtained very easily.
Questions
Solution
- $$M = 2, \hspace{0.1cm}f_{\rm G}/R_{\rm B} = 0.33\text{:} \hspace{0.2cm} \sigma_d/s_0 \ \hspace{0.15cm}\underline { = 0.047} \hspace{0.05cm},$$
- $$M = 4, \hspace{0.1cm}f_{\rm G}/R_{\rm B} = 0.28\text{:} \hspace{0.2cm} \sigma_d/s_0 \ \hspace{0.15cm}\underline { = 0.021} \hspace{0.05cm}.$$
(2) The optimum cutoff frequency is given when the quotient of the (half) eye opening and the noise rms value is maximum.
- The optimum results for the binary system for $f_{\rm G}/R_{\rm B} \underline {= 0.33}$:
- $$\rho_{\rm U,\hspace{0.05cm} max} = \frac{0.184^2}{ 0.047^2} = 15.32 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U,\hspace{0.05cm} max}\hspace{0.15cm}\underline { = 11.85\,{\rm dB}} \hspace{0.05cm}.$$
- In contrast, for the adjacent cutoff frequency values:
- $$f_{\rm G}/R_{\rm B} = 0.32\text{:} \hspace{0.2cm}\rho_{\rm U} = \frac{0.155^2}{ 0.040^2} = 15.02 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} = 11.76\,{\rm dB} \hspace{0.05cm},$$
- $$f_{\rm G}/R_{\rm B} = 0.34 \text{:} \hspace{0.2cm}\rho_{\rm U} = \frac{0.212^2}{ 0.055^2} = 14.86 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} = 11.72\,{\rm dB} \hspace{0.05cm}.$$
- From this, one can see the optimum, albeit a flat one.
(3) For $M = 4$, the following results are obtained:
- $$f_{\rm G}/R_{\rm B} = 0.27 \text{:} \hspace{0.2cm}\rho_{\rm U} = \frac{0.097^2}{ 0.017^2} = 32.56 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} = 15.13\,{\rm dB} \hspace{0.05cm},$$
- $$f_{\rm G}/R_{\rm B} = 0.28 \text{:} \hspace{0.2cm}\rho_{\rm U} = \frac{0.121^2}{ 0.021^2} = 33.20 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} \hspace{0.15cm}\underline {= 15.21\,{\rm dB}} \hspace{0.05cm},$$
- $$f_{\rm G}/R_{\rm B} = 0.29 \text{:} \hspace{0.2cm}\rho_{\rm U} = \frac{0.139^2}{ 0.025^2} = 30.91 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} = 14.90\,{\rm dB} \hspace{0.05cm}.$$
- Thus, the optimum cutoff frequency is $f_{\rm G}/R_{\rm B} \underline {= 0.28}$ for the quaternary system.
- The signal-to-noise ratio is then more than $3 \, {\rm dB}$ larger than for the binary system with optimized cutoff frequency.
(4) Statements 1, 3 and 4 are correct:
- The correctness of the first statement is confirmed by the table. For $f_{\rm G}/R_{\rm B} ≥ 0.35$, the binary system has a larger eye opening than the quaternary system. Moreover, by normalizing all frequencies to the bit rate, the noise rms value is independent of the level number $M$, so that the optimization can be restricted to the eye opening.
- For $f_{\rm G}/R_{\rm B} < 0.35$, on the other hand, the quaternary system is better, so also for $f_{\rm G}/R_{\rm B} = 0.33$. Although this cutoff frequency is optimal for $M = 2$ and not for $M = 4$, with $f_{\rm G}/R_{\rm B} = 0.33$ the quaternary system is better than the binary system by about $0.85 \, {\rm dB}$.
- The third statement is true. Due to the lower (more precisely: half) symbol rate, for $M = 4$ the eye is still open even with $f_{\rm G}/R_{\rm B} = 0.23$, while for a binary system there is already an (almost) closed eye for $f_{\rm G}/R_{\rm B} = 0.27$.
- With larger characteristic cable attenuation, the tendency goes to smaller and smaller cutoff frequency in order to keep the increase of the noise as small as possible. But if already at $a_* = 80 \, {\rm dB}$ the quaternary system (optimized with respect to cutoff frequency) is better, the same is true for $100 \, {\rm dB}$. The gain is larger than $15.21 - 11.85 \approx 3.4 \, {\rm dB}$. These values were obtained in questions (2) and (3).
- In contrast, no statement is possible for the characteristic cable attenuation $a_* = 40 \, {\rm dB}$ based on the available numerical material. A system simulation provided the following results for this $($for $E_{\rm B}/N_0 = 50 \, {\rm dB})$:
- $$M =2\text{:} \hspace{0.2cm}10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} = 15.43\,{\rm dB} \hspace{0.2cm}{\rm with}\hspace{0.2cm} f_{\rm G}/R_{\rm B} \approx 0.4 \hspace{0.05cm},$$
- $$M =4\text{:} \hspace{0.2cm}10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} = 14.65\,{\rm dB} \hspace{0.2cm}{\rm with}\hspace{0.2cm} f_{\rm G}/R_{\rm B} \approx 0.32 \hspace{0.05cm}.$$