Difference between revisions of "Aufgaben:Exercise 2.7: AMI Code"
m (Guenter moved page Aufgabe 2.7: AMI-Code to Exercise 2.7: AMI Code) |
|||
| (7 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite=Digital_Signal_Transmission/ | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Symbolwise_Coding_with_Pseudo-Ternary_Codes |
}} | }} | ||
| − | [[File: | + | [[File:EN_Dig_A_2_7.png|right|frame|Block diagram of a <br>pseudo-ternary encoder]] |
| − | The diagram shows the block diagram for AMI coding, assuming binary bipolar amplitude coefficients $q_{\nu} ∈ \{–1, +1\}$ at the input. This | + | The diagram shows the block diagram for AMI coding, assuming binary bipolar amplitude coefficients $q_{\nu} ∈ \{–1, +1\}$ at the input. This encoding is done in two stages: |
| − | + | #In the first part of the block diagram, a binary pre-encoded symbol $b_{\nu}$ is generated at each clock from the modulo-2 addition of $q_{\nu}$ and $b_{\nu -1}$. It holds $b_{\nu} ∈ \{–1, +1\}.$<br> | |
| − | + | #Then, the current amplitude coefficient of the ternary transmitted signal $s(t)$ is determined by a conventional subtraction. Thereby holds: | |
| − | :$$a_\nu = {1}/{2} \cdot \ | + | ::$$a_\nu = {1}/{2} \cdot \big [ b_\nu - b_{\nu-1} \big ] \hspace{0.05cm}.$$ |
| − | Due to AMI coding, it is ensured that | + | Due to AMI coding, it is ensured that the AMI encoder signal does not contain these two "long sequences"<br> |
| − | *In the HDB3 code, four consecutive zeros each are marked by a specific violation of the AMI coding rule. | + | $ \langle c_\nu \rangle = \langle \text{...}, +1, +1, +1, +1, +1, \text{...}\rangle$ resp. |
| − | *In the B6ZS code, six consecutive zeros are marked by a targeted violation of the AMI coding rule. | + | |
| + | $ \langle c_\nu \rangle = \langle \text{...}, -1, -1, -1, -1, -1, \text{...}\rangle$. | ||
| + | |||
| + | Modified AMI codes have also been developed to avoid long "zero sequences": | ||
| + | *In the HDB3 code, four consecutive zeros each are marked by a specific violation of the AMI coding rule. | ||
| + | |||
| + | *In the B6ZS code, six consecutive zeros are marked by a targeted violation of the AMI coding rule. | ||
| Line 20: | Line 26: | ||
| − | + | Notes: | |
| − | + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/Symbolwise_Coding_with_Pseudo-Ternary_Codes|"Symbolwise Coding with Pseudo-Ternary Codes"]]. | |
| − | |||
| − | *The exercise belongs to the chapter [[Digital_Signal_Transmission/ | ||
| − | *You can check the results with the | + | *You can check the results with the (German language) SWF applet [[Applets:Pseudoternaercodierung|"Signals, ACF and PSD of pseudo-ternary codes"]]. |
| Line 31: | Line 35: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {At the input, $\langle q_{\nu} \rangle = \langle +1, –1, +1, +1, –1, +1, +1, –1, –1, –1, –1, +1 \rangle$ is applied. Determine the binary | + | {At the input, $\langle q_{\nu} \rangle = \langle +1, –1, +1, +1, –1, +1, +1, –1, –1, –1, –1, +1 \rangle$ is applied. <br>Determine the binary pre-encoded sequence $\langle b_{\nu} \rangle$ with the default $b_{0} = \hspace{0.05cm}-1$. Enter the following values as a check: |
|type="{}"} | |type="{}"} | ||
$b_{1} \hspace{0.26cm} = \ $ { 1 3% } | $b_{1} \hspace{0.26cm} = \ $ { 1 3% } | ||
| Line 37: | Line 41: | ||
$b_{12} \ = \ $ { -1.03--0.97 } | $b_{12} \ = \ $ { -1.03--0.97 } | ||
| − | {Furthermore, determine the sequence $\langle a_{\nu} \rangle$ of the amplitude coefficients of the AMI- | + | {Furthermore, determine the sequence $\langle a_{\nu} \rangle$ of the amplitude coefficients of the AMI-encoded transmitted signal $s(t)$. <br>Enter the following values to check the results: |
|type="{}"} | |type="{}"} | ||
$a_{1} \hspace{0.28cm} = \ $ { 1 3% } | $a_{1} \hspace{0.28cm} = \ $ { 1 3% } | ||
| Line 60: | Line 64: | ||
$\E\big[a_{\nu}^{2}\big] \ = \ $ { 0.5 3% } | $\E\big[a_{\nu}^{2}\big] \ = \ $ { 0.5 3% } | ||
| − | {Calculate the auto-correlation function $\varphi_{a}(\lambda)$, in particular the following ACF values: | + | {Calculate the auto-correlation function $\varphi_{a}(\lambda)$, in particular the following ACF values: |
|type="{}"} | |type="{}"} | ||
$\varphi_{a}(\lambda = 0) \ = \ $ { 0.5 3% } | $\varphi_{a}(\lambda = 0) \ = \ $ { 0.5 3% } | ||
| Line 66: | Line 70: | ||
$\varphi_{a}(\lambda = 2) \ = \ $ { 0. } | $\varphi_{a}(\lambda = 2) \ = \ $ { 0. } | ||
| − | {What is the power-spectral density ${\it \Phi}_{a}(f)$? What are the values for $f = 0$ and $f = 1/(2T)$? | + | {What is the power-spectral density ${\it \Phi}_{a}(f)$? What are the values for $f = 0$ and $f = 1/(2T)$? |
|type="{}"} | |type="{}"} | ||
${\it \Phi}_{a}(f = 0) \ = \ $ { 0. } | ${\it \Phi}_{a}(f = 0) \ = \ $ { 0. } | ||
| Line 76: | Line 80: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' The modulo-2 addition can also be taken as an antivalence. | + | '''(1)''' The modulo-2 addition can also be taken as an "antivalence". |
| − | *It is $b_{\nu} = +1$ if $q_{\nu}$ and $b_{\nu – 1}$ differ, otherwise set $b_{\nu} = -1$. | + | *It is $b_{\nu} = +1$ if $q_{\nu}$ and $b_{\nu – 1}$ differ, otherwise set $b_{\nu} = -1$. |
| − | *With the initial value $b_{0} = -1$ we obtain: | + | *With the initial value $b_{0} = -1$ we obtain: |
:$$b_1\hspace{0.15cm}\underline { = +1}, \hspace{0.2cm} b_2 = +1, \hspace{0.2cm}b_3 = -1, \hspace{0.2cm}b_4 = +1, \hspace{0.2cm}b_5 = +1, \hspace{0.2cm}b_6 = -1\hspace{0.05cm},$$ | :$$b_1\hspace{0.15cm}\underline { = +1}, \hspace{0.2cm} b_2 = +1, \hspace{0.2cm}b_3 = -1, \hspace{0.2cm}b_4 = +1, \hspace{0.2cm}b_5 = +1, \hspace{0.2cm}b_6 = -1\hspace{0.05cm},$$ | ||
:$$b_7 = +1, \hspace{0.2cm} b_8 = +1, \hspace{0.2cm}b_9 = +1, \hspace{0.2cm}b_{10} = +1, \hspace{0.2cm}b_{11} \hspace{0.15cm}\underline {= +1}, \hspace{0.2cm}b_{12} \hspace{0.15cm}\underline {= -1}\hspace{0.05cm}.$$ | :$$b_7 = +1, \hspace{0.2cm} b_8 = +1, \hspace{0.2cm}b_9 = +1, \hspace{0.2cm}b_{10} = +1, \hspace{0.2cm}b_{11} \hspace{0.15cm}\underline {= +1}, \hspace{0.2cm}b_{12} \hspace{0.15cm}\underline {= -1}\hspace{0.05cm}.$$ | ||
| Line 86: | Line 90: | ||
:$$a_1\hspace{0.15cm}\underline { = +1}, \hspace{0.2cm} a_2 = 0, \hspace{0.2cm}a_3 = -1, \hspace{0.2cm}a_4 = +1, \hspace{0.2cm}a_5 = 0, \hspace{0.2cm}a_6 = -1\hspace{0.05cm},$$ | :$$a_1\hspace{0.15cm}\underline { = +1}, \hspace{0.2cm} a_2 = 0, \hspace{0.2cm}a_3 = -1, \hspace{0.2cm}a_4 = +1, \hspace{0.2cm}a_5 = 0, \hspace{0.2cm}a_6 = -1\hspace{0.05cm},$$ | ||
:$$a_7 = +1, \hspace{0.2cm} a_8 = 0, \hspace{0.2cm}a_9 = 0, \hspace{0.2cm}a_{10} = 0, \hspace{0.2cm}a_{11}\hspace{0.15cm}\underline { = 0}, \hspace{0.2cm}a_{12} \hspace{0.15cm}\underline {= -1}\hspace{0.05cm}.$$ | :$$a_7 = +1, \hspace{0.2cm} a_8 = 0, \hspace{0.2cm}a_9 = 0, \hspace{0.2cm}a_{10} = 0, \hspace{0.2cm}a_{11}\hspace{0.15cm}\underline { = 0}, \hspace{0.2cm}a_{12} \hspace{0.15cm}\underline {= -1}\hspace{0.05cm}.$$ | ||
| − | This result is obtained by the equation $a_{\nu} = (b_{\nu} - b_{\nu –1})/2$ or by direct application of the AMI coding rule: | + | This result is obtained by the equation $a_{\nu} = (b_{\nu} - b_{\nu –1})/2$ or by direct application of the AMI coding rule: |
| − | *A source symbol $q_{\nu} = -1$ always leads to $a_{\nu} = 0$. | + | *A source symbol $q_{\nu} = -1$ always leads to $a_{\nu} = 0$. |
| − | * | + | *A source symbols $q_{\nu} = +1$ lead alternately to $a_{\nu} = +1$ and $a_{\nu} = -1$. |
| + | |||
| + | |||
| + | '''(3)''' <u>Solution 1</u> is correct: | ||
| + | *The AMI code yields four consecutive zeros in the range between $\nu = 8$ and $\nu = 11$. | ||
| + | *In the HDB3 code, these four symbols would be marked with "$+ 0 0 +$". Thus, the AMI rule is deliberately violated for identification purposes. | ||
| + | *In contrast, the B6ZS code substitutes only zero sequences over six symbols. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''(4)''' Assuming equally probable binary values $±1$, we obtain ${\Pr}(a_{\nu} = 0) = {\Pr}(q_{\nu} = -1)\hspace{0.15cm}\underline{ = 1/2}$ and for symmetry reasons | + | '''(4)''' Assuming equally probable binary values $±1$, we obtain ${\Pr}(a_{\nu} = 0) = {\Pr}(q_{\nu} = -1)\hspace{0.15cm}\underline{ = 1/2}$ and for symmetry reasons |
: ${\Pr}(a_{\nu} = +1) = {\Pr}(a_{\nu} = -1) \hspace{0.15cm}\underline{ = 1/4}.$ | : ${\Pr}(a_{\nu} = +1) = {\Pr}(a_{\nu} = -1) \hspace{0.15cm}\underline{ = 1/4}.$ | ||
| − | '''(5)''' Using the probabilities calculated in '''(4)''', we obtain: | + | |
| + | '''(5)''' Using the probabilities calculated in '''(4)''', we obtain: | ||
:$${\rm E}\big[a_\nu \big] = \ {1}/{4} \cdot (+1) +{1}/{2} \cdot 0+ {1}/{4} \cdot (-1)\hspace{0.15cm}\underline {= 0}\hspace{0.05cm},$$ | :$${\rm E}\big[a_\nu \big] = \ {1}/{4} \cdot (+1) +{1}/{2} \cdot 0+ {1}/{4} \cdot (-1)\hspace{0.15cm}\underline {= 0}\hspace{0.05cm},$$ | ||
:$$ {\rm E}\big[a_\nu^2 \big] = \ {1}/{4} \cdot (+1)^2 +{1}/{2} \cdot 0^2 + {1}/{4} \cdot (-1)^2 \hspace{0.15cm}\underline {= 0.5} \hspace{0.05cm}.$$ | :$$ {\rm E}\big[a_\nu^2 \big] = \ {1}/{4} \cdot (+1)^2 +{1}/{2} \cdot 0^2 + {1}/{4} \cdot (-1)^2 \hspace{0.15cm}\underline {= 0.5} \hspace{0.05cm}.$$ | ||
| − | '''(6)''' The ACF value at $\lambda = 0$ is equal to the | + | |
| + | '''(6)''' The ACF value at $\lambda = 0$ is equal to the second moment of the amplitude coefficients: | ||
:$$ \varphi_a(\lambda = 0) = {\rm E}[a_\nu^2] \hspace{0.15cm}\underline {= 0.5} \hspace{0.05cm}.$$ | :$$ \varphi_a(\lambda = 0) = {\rm E}[a_\nu^2] \hspace{0.15cm}\underline {= 0.5} \hspace{0.05cm}.$$ | ||
| − | *Since the order of the AMI code is $N = 1$, for $\lambda > 1$: $\varphi_a(\lambda > 1) = {\rm E}[a_\nu^2] \hspace{0.15cm}\underline {= 0} | + | *Since the order of the AMI code is $N = 1$, for $\lambda > 1$: $\varphi_a(\lambda > 1) = {\rm E}[a_\nu^2] \hspace{0.15cm}\underline {= 0} \hspace{0.05cm}.$ |
| − | |||
| − | |||
| − | * | + | *The ACF value $\varphi_{a}(\lambda = 1)$ must be determined by averaging: $\varphi_a(\lambda = 1) = {\rm E}[a_\nu \cdot a_{\nu+1} \cdot {\rm Pr}(a_\nu \cap a_{\nu+1})] \hspace{0.05cm}.$ |
| + | *Of the nine possible combinations for $a_{\nu} \cdot a_{\nu +1}$, only four yield a non-zero value. In the other cases, either $a_{\nu} = 0$ or $a_{\nu +1} = 0$. | ||
| − | However, since in AMI code also | + | *However, since in AMI code also |
:$${\rm Pr}[(a_\nu = +1) \cap (a_{\nu+1}= +1)] = \ 0 \hspace{0.05cm},$$ | :$${\rm Pr}[(a_\nu = +1) \cap (a_{\nu+1}= +1)] = \ 0 \hspace{0.05cm},$$ | ||
:$$ {\rm Pr}[(a_\nu = -1) \cap (a_{\nu+1}= -1)] = \ 0$$ | :$$ {\rm Pr}[(a_\nu = -1) \cap (a_{\nu+1}= -1)] = \ 0$$ | ||
| − | is true, | + | :is true, one obtains as the final result (since the ACF is always an even function): |
:$${\rm Pr}[(a_\nu = +1) \cap (a_{\nu+1}= -1)] = \ {\rm Pr}(a_\nu = +1)\cdot {\rm Pr}(a_{\nu+1} = -1 | a_\nu = +1) = {1}/{4}\cdot{1}/{2} ={1}/{8} \hspace{0.05cm},$$ | :$${\rm Pr}[(a_\nu = +1) \cap (a_{\nu+1}= -1)] = \ {\rm Pr}(a_\nu = +1)\cdot {\rm Pr}(a_{\nu+1} = -1 | a_\nu = +1) = {1}/{4}\cdot{1}/{2} ={1}/{8} \hspace{0.05cm},$$ | ||
:$${\rm Pr}[(a_\nu = -1) \cap (a_{\nu+1}= +1)] = \ {\rm Pr}(a_\nu = -1)\cdot {\rm Pr}(a_{\nu+1} = +1 | a_\nu = -1) = {1}/{4}\cdot {1}/{2} = {1}/{8}$$ | :$${\rm Pr}[(a_\nu = -1) \cap (a_{\nu+1}= +1)] = \ {\rm Pr}(a_\nu = -1)\cdot {\rm Pr}(a_{\nu+1} = +1 | a_\nu = -1) = {1}/{4}\cdot {1}/{2} = {1}/{8}$$ | ||
[[File:P_ID1353__Dig_A_2_7f.png|right|frame|Auto-correlation functions of the AMI code]] | [[File:P_ID1353__Dig_A_2_7f.png|right|frame|Auto-correlation functions of the AMI code]] | ||
| − | + | ||
| − | :$$\varphi_{a}(\lambda = +1) = \varphi_{a}(\lambda = | + | :$$\Rightarrow \hspace{0.3cm} \varphi_{a}(\lambda = +1) = \varphi_{a}(\lambda = -1) = -0.25.$$ |
| − | *This takes into account that $a_{\nu} = +1$ is followed by $a_{\nu +1} = +1$ and $a_{\nu +1} = -1$ with equal probability. | + | *This takes into account that $a_{\nu} = +1$ is followed by $a_{\nu +1} = +1$ and $a_{\nu +1} = -1$ with equal probability. Thus, the result is: |
| − | |||
:$$\varphi_a(\lambda = 0)\hspace{0.15cm}\underline {= 0.5} \hspace{0.05cm}, $$ | :$$\varphi_a(\lambda = 0)\hspace{0.15cm}\underline {= 0.5} \hspace{0.05cm}, $$ | ||
:$$\varphi_a(\lambda = 1)\hspace{0.15cm}\underline {= -0.25} \hspace{0.05cm},$$ | :$$\varphi_a(\lambda = 1)\hspace{0.15cm}\underline {= -0.25} \hspace{0.05cm},$$ | ||
:$$\varphi_a(\lambda = 2)\hspace{0.15cm}\underline {= 0}.$$ | :$$\varphi_a(\lambda = 2)\hspace{0.15cm}\underline {= 0}.$$ | ||
| − | + | ||
| + | |||
The graph shows | The graph shows | ||
| − | + | #the discrete ACF $\varphi_{a}(\lambda)$ of the amplitude coefficients, | |
| − | + | #the ACF $\varphi_{s}(\tau)$ of the transmitted signal under the condition of NRZ rectangular pulses and AMI coding. | |
| + | |||
| + | Here, the ACF $\varphi_{s}(\tau)$ (drawn in blue) is the result of the (discrete) convolution between the discrete ACF $\varphi_{a}(\lambda)$ (drawn in red) and the triangular energy ACF of the basic transmission pulse. | ||
| − | |||
| − | '''(7)''' From the given equation, taking into account the discrete ACF values calculated in '''(6)''' | + | '''(7)''' From the given equation, taking into account the discrete ACF values calculated in '''(6)''', |
:$$\varphi_{a}(\lambda = 0) = 1/2,$$ | :$$\varphi_{a}(\lambda = 0) = 1/2,$$ | ||
:$$\varphi_{a}(|\lambda| = 1) = -1/4,$$ | :$$\varphi_{a}(|\lambda| = 1) = -1/4,$$ | ||
| − | :$$\varphi_{a}(|\lambda| > 1) = 0$$ | + | :$$\varphi_{a}(|\lambda| > 1) = 0,$$ |
we obtain the following result: | we obtain the following result: | ||
:$${\it \Phi}_a(f) = \ \sum_{\lambda = -\infty}^{+\infty}\varphi_a(\lambda)\cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \lambda T} = \varphi_a(\lambda = 0) + 2 \cdot \varphi_a(\lambda = 1 )\cdot\cos ( 2 \pi f \hspace{0.02cm} \lambda T) = \ {1}/{2} \cdot \left [ 1 - \cos ( 2 \pi f \hspace{0.02cm} T)\right ] = \sin^2 ( \pi f \hspace{0.02cm} T) \hspace{0.05cm}.$$ | :$${\it \Phi}_a(f) = \ \sum_{\lambda = -\infty}^{+\infty}\varphi_a(\lambda)\cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \lambda T} = \varphi_a(\lambda = 0) + 2 \cdot \varphi_a(\lambda = 1 )\cdot\cos ( 2 \pi f \hspace{0.02cm} \lambda T) = \ {1}/{2} \cdot \left [ 1 - \cos ( 2 \pi f \hspace{0.02cm} T)\right ] = \sin^2 ( \pi f \hspace{0.02cm} T) \hspace{0.05cm}.$$ | ||
| − | In particular | + | In particular holds: |
:$${\it \Phi}_a(f = 0) \hspace{0.15cm}\underline {= 0},$$ | :$${\it \Phi}_a(f = 0) \hspace{0.15cm}\underline {= 0},$$ | ||
:$${\it \Phi}_a(f = {1}/({2T})) = \sin^2 ({\pi}/{2})\hspace{0.15cm}\underline {= 1} \hspace{0.05cm}.$$ | :$${\it \Phi}_a(f = {1}/({2T})) = \sin^2 ({\pi}/{2})\hspace{0.15cm}\underline {= 1} \hspace{0.05cm}.$$ | ||
| Line 153: | Line 161: | ||
| − | [[Category:Digital Signal Transmission: Exercises|^2.4 | + | [[Category:Digital Signal Transmission: Exercises|^2.4 Pseudo-Ternary Codes^]] |
Latest revision as of 16:11, 25 May 2022
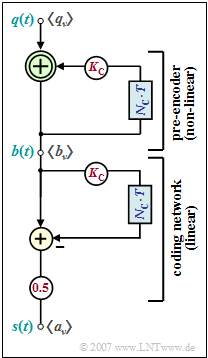
The diagram shows the block diagram for AMI coding, assuming binary bipolar amplitude coefficients $q_{\nu} ∈ \{–1, +1\}$ at the input. This encoding is done in two stages:
- In the first part of the block diagram, a binary pre-encoded symbol $b_{\nu}$ is generated at each clock from the modulo-2 addition of $q_{\nu}$ and $b_{\nu -1}$. It holds $b_{\nu} ∈ \{–1, +1\}.$
- Then, the current amplitude coefficient of the ternary transmitted signal $s(t)$ is determined by a conventional subtraction. Thereby holds:
- $$a_\nu = {1}/{2} \cdot \big [ b_\nu - b_{\nu-1} \big ] \hspace{0.05cm}.$$
Due to AMI coding, it is ensured that the AMI encoder signal does not contain these two "long sequences"
$ \langle c_\nu \rangle = \langle \text{...}, +1, +1, +1, +1, +1, \text{...}\rangle$ resp.
$ \langle c_\nu \rangle = \langle \text{...}, -1, -1, -1, -1, -1, \text{...}\rangle$.
Modified AMI codes have also been developed to avoid long "zero sequences":
- In the HDB3 code, four consecutive zeros each are marked by a specific violation of the AMI coding rule.
- In the B6ZS code, six consecutive zeros are marked by a targeted violation of the AMI coding rule.
The power-spectral density ${\it \Phi}_{a}(f)$ of the amplitude coefficients is to be obtained from the discrete ACF values $\varphi_{a}(\lambda) = {\E}\big[a_{\nu} \cdot a_{\nu + \lambda}\big]$. The Fourier transform in discrete representation is:
- $${\it \Phi}_a(f) = \sum_{\lambda = -\infty}^{+\infty}\varphi_a(\lambda)\cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \lambda T} \hspace{0.05cm}.$$
Notes:
- The exercise belongs to the chapter "Symbolwise Coding with Pseudo-Ternary Codes".
- You can check the results with the (German language) SWF applet "Signals, ACF and PSD of pseudo-ternary codes".
Questions
Solution
- It is $b_{\nu} = +1$ if $q_{\nu}$ and $b_{\nu – 1}$ differ, otherwise set $b_{\nu} = -1$.
- With the initial value $b_{0} = -1$ we obtain:
- $$b_1\hspace{0.15cm}\underline { = +1}, \hspace{0.2cm} b_2 = +1, \hspace{0.2cm}b_3 = -1, \hspace{0.2cm}b_4 = +1, \hspace{0.2cm}b_5 = +1, \hspace{0.2cm}b_6 = -1\hspace{0.05cm},$$
- $$b_7 = +1, \hspace{0.2cm} b_8 = +1, \hspace{0.2cm}b_9 = +1, \hspace{0.2cm}b_{10} = +1, \hspace{0.2cm}b_{11} \hspace{0.15cm}\underline {= +1}, \hspace{0.2cm}b_{12} \hspace{0.15cm}\underline {= -1}\hspace{0.05cm}.$$
(2) AMI coding gives the following amplitude coefficients:
- $$a_1\hspace{0.15cm}\underline { = +1}, \hspace{0.2cm} a_2 = 0, \hspace{0.2cm}a_3 = -1, \hspace{0.2cm}a_4 = +1, \hspace{0.2cm}a_5 = 0, \hspace{0.2cm}a_6 = -1\hspace{0.05cm},$$
- $$a_7 = +1, \hspace{0.2cm} a_8 = 0, \hspace{0.2cm}a_9 = 0, \hspace{0.2cm}a_{10} = 0, \hspace{0.2cm}a_{11}\hspace{0.15cm}\underline { = 0}, \hspace{0.2cm}a_{12} \hspace{0.15cm}\underline {= -1}\hspace{0.05cm}.$$
This result is obtained by the equation $a_{\nu} = (b_{\nu} - b_{\nu –1})/2$ or by direct application of the AMI coding rule:
- A source symbol $q_{\nu} = -1$ always leads to $a_{\nu} = 0$.
- A source symbols $q_{\nu} = +1$ lead alternately to $a_{\nu} = +1$ and $a_{\nu} = -1$.
(3) Solution 1 is correct:
- The AMI code yields four consecutive zeros in the range between $\nu = 8$ and $\nu = 11$.
- In the HDB3 code, these four symbols would be marked with "$+ 0 0 +$". Thus, the AMI rule is deliberately violated for identification purposes.
- In contrast, the B6ZS code substitutes only zero sequences over six symbols.
(4) Assuming equally probable binary values $±1$, we obtain ${\Pr}(a_{\nu} = 0) = {\Pr}(q_{\nu} = -1)\hspace{0.15cm}\underline{ = 1/2}$ and for symmetry reasons
- ${\Pr}(a_{\nu} = +1) = {\Pr}(a_{\nu} = -1) \hspace{0.15cm}\underline{ = 1/4}.$
(5) Using the probabilities calculated in (4), we obtain:
- $${\rm E}\big[a_\nu \big] = \ {1}/{4} \cdot (+1) +{1}/{2} \cdot 0+ {1}/{4} \cdot (-1)\hspace{0.15cm}\underline {= 0}\hspace{0.05cm},$$
- $$ {\rm E}\big[a_\nu^2 \big] = \ {1}/{4} \cdot (+1)^2 +{1}/{2} \cdot 0^2 + {1}/{4} \cdot (-1)^2 \hspace{0.15cm}\underline {= 0.5} \hspace{0.05cm}.$$
(6) The ACF value at $\lambda = 0$ is equal to the second moment of the amplitude coefficients:
- $$ \varphi_a(\lambda = 0) = {\rm E}[a_\nu^2] \hspace{0.15cm}\underline {= 0.5} \hspace{0.05cm}.$$
- Since the order of the AMI code is $N = 1$, for $\lambda > 1$: $\varphi_a(\lambda > 1) = {\rm E}[a_\nu^2] \hspace{0.15cm}\underline {= 0} \hspace{0.05cm}.$
- The ACF value $\varphi_{a}(\lambda = 1)$ must be determined by averaging: $\varphi_a(\lambda = 1) = {\rm E}[a_\nu \cdot a_{\nu+1} \cdot {\rm Pr}(a_\nu \cap a_{\nu+1})] \hspace{0.05cm}.$
- Of the nine possible combinations for $a_{\nu} \cdot a_{\nu +1}$, only four yield a non-zero value. In the other cases, either $a_{\nu} = 0$ or $a_{\nu +1} = 0$.
- However, since in AMI code also
- $${\rm Pr}[(a_\nu = +1) \cap (a_{\nu+1}= +1)] = \ 0 \hspace{0.05cm},$$
- $$ {\rm Pr}[(a_\nu = -1) \cap (a_{\nu+1}= -1)] = \ 0$$
- is true, one obtains as the final result (since the ACF is always an even function):
- $${\rm Pr}[(a_\nu = +1) \cap (a_{\nu+1}= -1)] = \ {\rm Pr}(a_\nu = +1)\cdot {\rm Pr}(a_{\nu+1} = -1 | a_\nu = +1) = {1}/{4}\cdot{1}/{2} ={1}/{8} \hspace{0.05cm},$$
- $${\rm Pr}[(a_\nu = -1) \cap (a_{\nu+1}= +1)] = \ {\rm Pr}(a_\nu = -1)\cdot {\rm Pr}(a_{\nu+1} = +1 | a_\nu = -1) = {1}/{4}\cdot {1}/{2} = {1}/{8}$$
- $$\Rightarrow \hspace{0.3cm} \varphi_{a}(\lambda = +1) = \varphi_{a}(\lambda = -1) = -0.25.$$
- This takes into account that $a_{\nu} = +1$ is followed by $a_{\nu +1} = +1$ and $a_{\nu +1} = -1$ with equal probability. Thus, the result is:
- $$\varphi_a(\lambda = 0)\hspace{0.15cm}\underline {= 0.5} \hspace{0.05cm}, $$
- $$\varphi_a(\lambda = 1)\hspace{0.15cm}\underline {= -0.25} \hspace{0.05cm},$$
- $$\varphi_a(\lambda = 2)\hspace{0.15cm}\underline {= 0}.$$
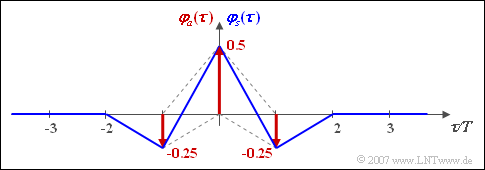
The graph shows
- the discrete ACF $\varphi_{a}(\lambda)$ of the amplitude coefficients,
- the ACF $\varphi_{s}(\tau)$ of the transmitted signal under the condition of NRZ rectangular pulses and AMI coding.
Here, the ACF $\varphi_{s}(\tau)$ (drawn in blue) is the result of the (discrete) convolution between the discrete ACF $\varphi_{a}(\lambda)$ (drawn in red) and the triangular energy ACF of the basic transmission pulse.
(7) From the given equation, taking into account the discrete ACF values calculated in (6),
- $$\varphi_{a}(\lambda = 0) = 1/2,$$
- $$\varphi_{a}(|\lambda| = 1) = -1/4,$$
- $$\varphi_{a}(|\lambda| > 1) = 0,$$
we obtain the following result:
- $${\it \Phi}_a(f) = \ \sum_{\lambda = -\infty}^{+\infty}\varphi_a(\lambda)\cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \lambda T} = \varphi_a(\lambda = 0) + 2 \cdot \varphi_a(\lambda = 1 )\cdot\cos ( 2 \pi f \hspace{0.02cm} \lambda T) = \ {1}/{2} \cdot \left [ 1 - \cos ( 2 \pi f \hspace{0.02cm} T)\right ] = \sin^2 ( \pi f \hspace{0.02cm} T) \hspace{0.05cm}.$$
In particular holds:
- $${\it \Phi}_a(f = 0) \hspace{0.15cm}\underline {= 0},$$
- $${\it \Phi}_a(f = {1}/({2T})) = \sin^2 ({\pi}/{2})\hspace{0.15cm}\underline {= 1} \hspace{0.05cm}.$$