Difference between revisions of "Aufgaben:Exercise 4.16: Binary Frequency Shift Keying"
| (One intermediate revision by one other user not shown) | |||
| Line 81: | Line 81: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
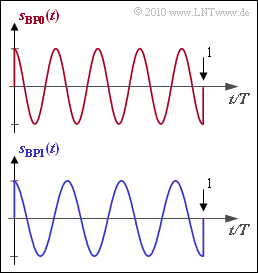
| − | '''(1)''' By counting the oscillations within a symbol duration $T$, the two frequencies $f_0 = 4.5/T$ and $f_1 = 3.5/T$ are obtained. | + | '''(1)''' By counting the oscillations within a symbol duration $T$, the two frequencies $f_0 = 4.5/T$ and $f_1 = 3.5/T$ are obtained. |
| − | *From this carrier frequencies and frequency | + | |
| + | *From this carrier frequencies and frequency deviations are calculated to | ||
:$$f_{\rm T} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {1}/{2}\cdot (f_0 + f_1) = \underline{4 \cdot 1/T}\hspace{0.05cm},$$ | :$$f_{\rm T} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {1}/{2}\cdot (f_0 + f_1) = \underline{4 \cdot 1/T}\hspace{0.05cm},$$ | ||
:$$ \Delta f_{\rm A} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {1}/{2}\cdot (f_0 - f_1)= \underline{0.5 \cdot 1/T }\hspace{0.05cm}.$$ | :$$ \Delta f_{\rm A} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {1}/{2}\cdot (f_0 - f_1)= \underline{0.5 \cdot 1/T }\hspace{0.05cm}.$$ | ||
| − | '''(2)''' With the given equation, the modulation index is: | + | '''(2)''' With the given equation, the modulation index is: |
:$$h = 2 \cdot \Delta f_{\rm A} \cdot T = 2 \cdot 0.5 \cdot 1/T \cdot T \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{h= 1}\hspace{0.05cm}. $$ | :$$h = 2 \cdot \Delta f_{\rm A} \cdot T = 2 \cdot 0.5 \cdot 1/T \cdot T \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{h= 1}\hspace{0.05cm}. $$ | ||
| Line 96: | Line 97: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Orthogonality means that this inner product must be $0$: | + | Orthogonality means that this inner product must be $0$: |
:$$< \hspace{-0.05cm} s_{\rm TP0}(t) \cdot s_{\rm TP1}(t) \hspace{-0.05cm} > \hspace{0.2cm} = | :$$< \hspace{-0.05cm} s_{\rm TP0}(t) \cdot s_{\rm TP1}(t) \hspace{-0.05cm} > \hspace{0.2cm} = | ||
\frac{E}{{\rm j}2\pi h} \cdot \left [ {\rm e}^{\hspace{0.05cm}{\rm j} 2\pi h} - 1 \right ] = 0 | \frac{E}{{\rm j}2\pi h} \cdot \left [ {\rm e}^{\hspace{0.05cm}{\rm j} 2\pi h} - 1 \right ] = 0 | ||
\hspace{0.3cm}\Rightarrow \hspace{0.3cm} h = 1, 2, 3, ...$$ | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} h = 1, 2, 3, ...$$ | ||
| − | Consequently, <u>solutions 3 and 4</u> are correct: | + | Consequently, <u>solutions 3 and 4</u> are correct: |
| − | *If the modulation index $h$ is integer, non-coherent demodulation can be performed without violating orthogonality. | + | *If the modulation index $h$ is integer, non-coherent demodulation can be performed without violating orthogonality. |
'''(4)''' <u>Solutions 1, 3 and 4</u> are correct: | '''(4)''' <u>Solutions 1, 3 and 4</u> are correct: | ||
| − | *For the inner product of the band–pass signals, according to the explanations in the information section, it can be written: | + | *For the inner product of the band–pass signals, according to the explanations in the information section, it can be written: |
:$$< \hspace{-0.05cm}s_{\rm BP0}(t) \hspace{0.01cm} \ \cdot \ \hspace{0.01cm} s_{\rm BP1}(t) \hspace{-0.05cm}> \hspace{0.2cm}= | :$$< \hspace{-0.05cm}s_{\rm BP0}(t) \hspace{0.01cm} \ \cdot \ \hspace{0.01cm} s_{\rm BP1}(t) \hspace{-0.05cm}> \hspace{0.2cm}= | ||
{\rm Re}\left [ \hspace{0.1cm}< \hspace{-0.05cm}s_{\rm TP0}(t) \cdot s_{\rm TP1}(t) \hspace{-0.05cm}> \hspace{0.2cm} \right ] = {\rm Re}\left [ \frac{E}{{\rm j}2\pi h} \cdot \left ( {\rm e}^{\hspace{0.05cm}{\rm j} 2\pi h} - 1 \right ) \right ]$$ | {\rm Re}\left [ \hspace{0.1cm}< \hspace{-0.05cm}s_{\rm TP0}(t) \cdot s_{\rm TP1}(t) \hspace{-0.05cm}> \hspace{0.2cm} \right ] = {\rm Re}\left [ \frac{E}{{\rm j}2\pi h} \cdot \left ( {\rm e}^{\hspace{0.05cm}{\rm j} 2\pi h} - 1 \right ) \right ]$$ | ||
:$$ \Rightarrow\hspace{0.3cm}< \hspace{-0.05cm}s_{\rm BP0}(t) \hspace{0.01cm} \ \cdot \ \hspace{0.01cm} s_{\rm BP1}(t) \hspace{-0.05cm}> \hspace{0.2cm}= {\rm Re}\left [ \frac{E}{2\pi h} \cdot \left ( \sin( 2\pi h) - {\rm j} \cdot [\cos( 2\pi h) - 1 ]\right ) \right ] = \frac{E \cdot \sin( 2\pi h)}{2\pi h} \hspace{0.05cm}.$$ | :$$ \Rightarrow\hspace{0.3cm}< \hspace{-0.05cm}s_{\rm BP0}(t) \hspace{0.01cm} \ \cdot \ \hspace{0.01cm} s_{\rm BP1}(t) \hspace{-0.05cm}> \hspace{0.2cm}= {\rm Re}\left [ \frac{E}{2\pi h} \cdot \left ( \sin( 2\pi h) - {\rm j} \cdot [\cos( 2\pi h) - 1 ]\right ) \right ] = \frac{E \cdot \sin( 2\pi h)}{2\pi h} \hspace{0.05cm}.$$ | ||
| − | *This result is $0$ whenever the modulation index $h$ is an integer multiple of $0.5$. | + | *This result is $0$ whenever the modulation index $h$ is an integer multiple of $0.5$. |
| + | |||
| + | '''(5)''' <u>Solution 2</u> is correct. | ||
| + | *For coherent demodulation, $h$ must be a multiple of $0.5$. | ||
| + | |||
| + | *If non-coherent demodulation is possible, as for example in the case considered here ($h = 1$), coherent demodulation is also applicable. | ||
| − | + | *In contrast, for $h = 0.5$, coherent demodulation can be applied, but non-coherent demodulation (which relies on the envelope) fails. | |
| − | |||
| − | |||
| − | *In contrast, for $h = 0.5$, coherent demodulation can be applied, but non-coherent demodulation (which relies on the envelope) fails. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 20:51, 1 September 2022
In binary FSK, the two messages $m_0$ and $m_1$ are represented by two different frequencies. For the two possible band–pass signals then applies in each case in the range $0 ≤ t ≤ T$ with $f_0 = f_{\rm T} + \Delta f_{\rm A}$ as well as $f_1 = f_{\rm T} \, – \Delta f_{\rm A}$:
- $$s_{\rm BP0}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{2E/T} \cdot \cos( 2\pi f_0 t)\hspace{0.05cm},$$
- $$ s_{\rm BP1}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{2E/T} \cdot \cos( 2\pi f_1 t)\hspace{0.05cm}.$$
The graph shows example signals $($in each case only of one symbol duration $T)$.
- In the above equation, $f_{\rm T}$ indicates the "carrier frequency" and $\Delta f_{\rm A}$ indicates the "frequency deviation" as the maximum deviation of the "instantaneous frequency" from the carrier frequency.
- $E$ is the signal energy. Here, it is equally true for the "average symbol energy" and the "average bit energy":
- $$E_{\rm S} = E_{\rm B} = E\hspace{0.05cm}.$$
Mostly one works with the "modulation index", which is defined as the ratio of total frequency deviation and symbol rate:
- $$h = \frac{2 \cdot \Delta f_{\rm A}}{1/T} = 2 \cdot \Delta f_{\rm A} \cdot T \hspace{0.05cm}.$$
Using $h$, the equivalent low-pass representation leads to the two complex signals
- $$ s_{\rm TP0}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{E/T} \cdot {\rm e}^{\hspace{0.05cm}+{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} \pi \hspace{0.03cm}\cdot \hspace{0.03cm} h \hspace{0.03cm}\cdot \hspace{0.03cm}t/T}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm},$$
- $$ s_{\rm TP1}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{E/T} \cdot {\rm e}^{\hspace{0.05cm}-{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} \pi \hspace{0.03cm}\cdot \hspace{0.03cm} h \hspace{0.03cm}\cdot \hspace{0.03cm}t/T}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm}.$$
An orthogonal FSK exists when the inner product gives the value $0$:
- $$< \hspace{-0.05cm}s_{\rm TP0}(t) \cdot s_{\rm TP1}(t) \hspace{-0.05cm}> \hspace{0.2cm}= \int_{0}^{T} s_{\rm TP0}(t) \cdot s_{\rm TP1}^{\star}(t) \,{\rm d} t =0 \hspace{0.05cm}.$$
In this case, non-coherent demodulation as described in the chapter "Carrier Frequency Systems with Non-Coherent Demodulation" is also possible.
The inner product of the band–pass signals can be determined from the inner product of the low–pass signals by real partitioning:
- $$< \hspace{-0.05cm}s_{\rm BP0}(t) \cdot s_{\rm BP1}(t) \hspace{-0.05cm}> \hspace{0.2cm}= {\rm Re}\left [ \hspace{0.1cm}< \hspace{-0.05cm}s_{\rm TP0}(t) \cdot s_{\rm TP1}(t) \hspace{-0.05cm}> \hspace{0.15cm} \right ]\hspace{0.05cm}.$$
If $〈 s_{\rm BP0}(t) \cdot s_{\rm BP1}(t)〉 = 0$, but at the same time $〈 s_{\rm TP0}(t) \cdot s_{\rm TP1}(t)〉 ≠ 0$,
- so coherent demodulation is possible,
- but no non-coherent demodulation.
Notes:
- The exercise belongs to the chapter "Carrier Frequency Systems with Coherent Demodulation".
- Reference is made in particular to the sections "Binary Frequency Shift Keying" $\rm (BFSK)$ and "Minimum Shift Keying" $\rm (MSK)$.
Questions
Solution
- From this carrier frequencies and frequency deviations are calculated to
- $$f_{\rm T} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {1}/{2}\cdot (f_0 + f_1) = \underline{4 \cdot 1/T}\hspace{0.05cm},$$
- $$ \Delta f_{\rm A} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {1}/{2}\cdot (f_0 - f_1)= \underline{0.5 \cdot 1/T }\hspace{0.05cm}.$$
(2) With the given equation, the modulation index is:
- $$h = 2 \cdot \Delta f_{\rm A} \cdot T = 2 \cdot 0.5 \cdot 1/T \cdot T \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{h= 1}\hspace{0.05cm}. $$
(3) The inner product of the low–pass signals is:
- $$< \hspace{-0.05cm} s_{\rm TP0}(t) \hspace{0.01cm} \ \cdot \ \hspace{0.01cm} s_{\rm TP1}(t) \hspace{-0.05cm} > \hspace{0.2cm} = \int_{0}^{T} s_{\rm TP0}(t) \cdot s_{\rm TP1}^{\star}(t) \,{\rm d} t = \frac{E}{T} \cdot \int_{0}^{T} {\rm e}^{\hspace{0.05cm}{\rm j} 2\pi h \hspace{0.03cm}\cdot \hspace{0.03cm}t/T} \,{\rm d} t = \frac{E}{{\rm j}2\pi h} \cdot \left [ {\rm e}^{\hspace{0.05cm}{\rm j} 2\pi h} - 1 \right ] \hspace{0.05cm}.$$
Orthogonality means that this inner product must be $0$:
- $$< \hspace{-0.05cm} s_{\rm TP0}(t) \cdot s_{\rm TP1}(t) \hspace{-0.05cm} > \hspace{0.2cm} = \frac{E}{{\rm j}2\pi h} \cdot \left [ {\rm e}^{\hspace{0.05cm}{\rm j} 2\pi h} - 1 \right ] = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} h = 1, 2, 3, ...$$
Consequently, solutions 3 and 4 are correct:
- If the modulation index $h$ is integer, non-coherent demodulation can be performed without violating orthogonality.
(4) Solutions 1, 3 and 4 are correct:
- For the inner product of the band–pass signals, according to the explanations in the information section, it can be written:
- $$< \hspace{-0.05cm}s_{\rm BP0}(t) \hspace{0.01cm} \ \cdot \ \hspace{0.01cm} s_{\rm BP1}(t) \hspace{-0.05cm}> \hspace{0.2cm}= {\rm Re}\left [ \hspace{0.1cm}< \hspace{-0.05cm}s_{\rm TP0}(t) \cdot s_{\rm TP1}(t) \hspace{-0.05cm}> \hspace{0.2cm} \right ] = {\rm Re}\left [ \frac{E}{{\rm j}2\pi h} \cdot \left ( {\rm e}^{\hspace{0.05cm}{\rm j} 2\pi h} - 1 \right ) \right ]$$
- $$ \Rightarrow\hspace{0.3cm}< \hspace{-0.05cm}s_{\rm BP0}(t) \hspace{0.01cm} \ \cdot \ \hspace{0.01cm} s_{\rm BP1}(t) \hspace{-0.05cm}> \hspace{0.2cm}= {\rm Re}\left [ \frac{E}{2\pi h} \cdot \left ( \sin( 2\pi h) - {\rm j} \cdot [\cos( 2\pi h) - 1 ]\right ) \right ] = \frac{E \cdot \sin( 2\pi h)}{2\pi h} \hspace{0.05cm}.$$
- This result is $0$ whenever the modulation index $h$ is an integer multiple of $0.5$.
(5) Solution 2 is correct.
- For coherent demodulation, $h$ must be a multiple of $0.5$.
- If non-coherent demodulation is possible, as for example in the case considered here ($h = 1$), coherent demodulation is also applicable.
- In contrast, for $h = 0.5$, coherent demodulation can be applied, but non-coherent demodulation (which relies on the envelope) fails.