Difference between revisions of "Aufgaben:Exercise 2.5Z: Some Calculations about GF(2 power 3)"
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{quiz-Header|Buchseite=Channel_Coding/Extension_Field}} | {{quiz-Header|Buchseite=Channel_Coding/Extension_Field}} | ||
| − | [[File: | + | [[File:EN_KC_Z_2_5_neu.png|right|frame| $\rm GF(2^3)$ elements; polynomial $p(x) = x^3 + x + 1$ ]] |
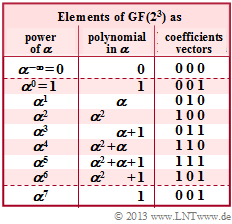
| − | We | + | We consider the extension field with eight elements ⇒ $\rm GF(2^3)$ according to the adjacent table. Since the underlying polynomial |
:$$p(x) = x^3 + x +1 $$ | :$$p(x) = x^3 + x +1 $$ | ||
| − | + | is both, irreducible and primitive, the Galois field can be stated in the following form: | |
| − | is both irreducible and primitive, the Galois field | ||
:$${\rm GF}(2^3) = \{\hspace{0.1cm}0\hspace{0.05cm},\hspace{0.1cm} 1,\hspace{0.05cm}\hspace{0.1cm} | :$${\rm GF}(2^3) = \{\hspace{0.1cm}0\hspace{0.05cm},\hspace{0.1cm} 1,\hspace{0.05cm}\hspace{0.1cm} | ||
\alpha\hspace{0.05cm},\hspace{0.1cm} \alpha^{2}\hspace{0.05cm},\hspace{0.1cm} \alpha^{3}\hspace{0.05cm},\hspace{0.1cm} \alpha^{4}\hspace{0.05cm},\hspace{0.1cm} \alpha^{5}\hspace{0.05cm},\hspace{0.1cm} \alpha^{6}\hspace{0.1cm}\}\hspace{0.05cm}. $$ | \alpha\hspace{0.05cm},\hspace{0.1cm} \alpha^{2}\hspace{0.05cm},\hspace{0.1cm} \alpha^{3}\hspace{0.05cm},\hspace{0.1cm} \alpha^{4}\hspace{0.05cm},\hspace{0.1cm} \alpha^{5}\hspace{0.05cm},\hspace{0.1cm} \alpha^{6}\hspace{0.1cm}\}\hspace{0.05cm}. $$ | ||
| − | The element $\alpha$ results thereby as solution of the equation $p(\alpha) = 0$ in the Galois field $\rm GF(2)$. | + | The element $\alpha$ results thereby as solution of the equation $p(\alpha) = 0$ in the Galois field $\rm GF(2)$. |
*This gives the following constraint: | *This gives the following constraint: | ||
:$$\alpha^3 + \alpha +1 = 0\hspace{0.3cm} \Rightarrow\hspace{0.3cm} \alpha^3 = \alpha +1\hspace{0.05cm}.$$ | :$$\alpha^3 + \alpha +1 = 0\hspace{0.3cm} \Rightarrow\hspace{0.3cm} \alpha^3 = \alpha +1\hspace{0.05cm}.$$ | ||
| Line 18: | Line 17: | ||
:$$\alpha^6 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^5 = \alpha \cdot (\alpha^2 +\alpha + 1)= \alpha^3 + \alpha^2 + \alpha= \alpha + 1 + \alpha^2 + \alpha = \alpha^2+ 1\hspace{0.05cm}.$$ | :$$\alpha^6 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^5 = \alpha \cdot (\alpha^2 +\alpha + 1)= \alpha^3 + \alpha^2 + \alpha= \alpha + 1 + \alpha^2 + \alpha = \alpha^2+ 1\hspace{0.05cm}.$$ | ||
| − | In this exercise you are to do some algebraic transformations in the Galois field $\rm GF(2^3)$ | + | In this exercise you are to do some algebraic transformations in the Galois field $\rm GF(2^3)$. |
| + | *Among other things you are asked for the multiplicative inverse of the element $\alpha^4$. | ||
| + | |||
| + | *Then it must hold: | ||
:$$\alpha^4 \cdot {\rm Inv_M}( \alpha^4) = 1 \hspace{0.05cm}.$$ | :$$\alpha^4 \cdot {\rm Inv_M}( \alpha^4) = 1 \hspace{0.05cm}.$$ | ||
| + | Hints: | ||
| + | * This exercise belongs to the chapter [[Channel_Coding/Extension_Field|"Extension Field"]]. | ||
| − | + | * This exercise is intended as a supplement to the slightly more difficult [[Aufgaben:Exercise_2.5:_Three_Variants_of_GF(2_power_4)|"Exercise 2.5"]]. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | * This exercise is intended as a supplement to the slightly more difficult [[Aufgaben:Exercise_2.5:_Three_Variants_of_GF(2_power_4)|"Exercise 2.5"]] | ||
| Line 37: | Line 35: | ||
===Questions=== | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Which of the statements are true for the higher powers of $\alpha^{i} \ (i ≥ 7)$ | + | {Which of the statements are true for the higher powers of $\alpha^{i} \ (i ≥ 7)$ ? |
|type="[]"} | |type="[]"} | ||
+ $\alpha^7 = 1$, | + $\alpha^7 = 1$, | ||
| Line 52: | Line 50: | ||
- $A = \alpha^4$. | - $A = \alpha^4$. | ||
| − | {Which transformation is allowed for $B = \alpha^{16} - \alpha^{12} \cdot \alpha^3$ | + | {Which transformation is allowed for $B = \alpha^{16} - \alpha^{12} \cdot \alpha^3$ ? |
|type="()"} | |type="()"} | ||
- $B = 1$, | - $B = 1$, | ||
| Line 84: | Line 82: | ||
- $E = \alpha^4$. | - $E = \alpha^4$. | ||
| − | {What statements hold for the multiplicative inverse to $\alpha^2 + \alpha$? | + | {What statements hold for the multiplicative inverse to $\alpha^2 + \alpha$ ? |
|type="[]"} | |type="[]"} | ||
- ${\rm Inv_M}(\alpha^2 + \alpha) = 1$, | - ${\rm Inv_M}(\alpha^2 + \alpha) = 1$, | ||
| Line 94: | Line 92: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' For example, using the table given in the front, you can find: | + | '''(1)''' For example, using the table given in the front, you can find: |
:$$\alpha^7 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^6 = \alpha \cdot (\alpha^2 + 1) = \alpha^3 + \alpha = (\alpha + 1) + \alpha = 1 \hspace{0.05cm},$$ | :$$\alpha^7 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^6 = \alpha \cdot (\alpha^2 + 1) = \alpha^3 + \alpha = (\alpha + 1) + \alpha = 1 \hspace{0.05cm},$$ | ||
:$$\alpha^8 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^7 = \alpha \cdot 1 = \alpha\hspace{0.05cm},$$ | :$$\alpha^8 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^7 = \alpha \cdot 1 = \alpha\hspace{0.05cm},$$ | ||
:$$\alpha^{13} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^7 \cdot \alpha^6 = 1 \cdot \alpha^6 = \alpha^2 + 1\hspace{0.05cm}.$$ | :$$\alpha^{13} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^7 \cdot \alpha^6 = 1 \cdot \alpha^6 = \alpha^2 + 1\hspace{0.05cm}.$$ | ||
| − | The table can therefore be continued modulo $7$. This means: <u>All proposed solutions</u> are correct. | + | *The table can therefore be continued modulo $7$. |
| + | |||
| + | *This means: <u>All proposed solutions</u> are correct. | ||
| + | |||
| + | |||
| + | '''(2)''' Correct is the <u>proposed solution 2</u> because of | ||
| + | *$\alpha^8 = \alpha$ according to subtask '''(1)''', | ||
| + | *$\alpha^6 = \alpha^2 + 1$ $($according to the table$)$, and | ||
| + | *$-\alpha^2 = \alpha^2$ $($operations in the binary Galois field$)$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
So applies: | So applies: | ||
| Line 114: | Line 116: | ||
| − | '''(3)''' With $\alpha^{16} = \alpha^{16-14} = \alpha^2$ | + | '''(3)''' With $\alpha^{16} = \alpha^{16-14} = \alpha^2$ and $\alpha^{12} \cdot \alpha^3 = \alpha^{15} = \alpha^{15-14} = \alpha$ we obtain the <u>proposed solution 5</u>: |
:$$B = \alpha^2 + \alpha= \alpha^4 | :$$B = \alpha^2 + \alpha= \alpha^4 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| Line 120: | Line 122: | ||
| − | '''(4)''' It holds $\alpha^3 = \alpha + 1$ | + | '''(4)''' It holds $\alpha^3 = \alpha + 1$ ⇒ $C = \alpha^3 + \alpha = \alpha + 1 + \alpha = 1$ ⇒ <u>Proposed solution 1</u>. |
| − | '''(5)''' With $\alpha^4 = \alpha^2 + \alpha$ we obtain $D = \alpha^4 + \alpha = \alpha^2$ ⇒ <u>Proposed solution 3</u>. | + | '''(5)''' With $\alpha^4 = \alpha^2 + \alpha$ we obtain $D = \alpha^4 + \alpha = \alpha^2$ ⇒ <u>Proposed solution 3</u>. |
| − | '''(6)''' Correct is the <u>proposed solution 4</u>: | + | '''(6)''' Correct is the <u>proposed solution 4</u>: |
:$$E = A \cdot B \cdot C/D = \alpha \cdot \alpha^4 \cdot 1/\alpha^2 = \alpha^3 | :$$E = A \cdot B \cdot C/D = \alpha \cdot \alpha^4 \cdot 1/\alpha^2 = \alpha^3 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | '''(7)''' According to the table, $\alpha^2 + \alpha = \alpha^4$ holds. Therefore must be valid: | + | '''(7)''' According to the table, $\alpha^2 + \alpha = \alpha^4$ holds. Therefore must be valid: |
:$$\alpha^4 \cdot {\rm Inv_M}( \alpha^4) = 1 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} | :$$\alpha^4 \cdot {\rm Inv_M}( \alpha^4) = 1 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} | ||
{\rm Inv_M}( \alpha^2 + \alpha) = {\rm Inv_M}( \alpha^4) = \alpha^{-4} = \alpha^3 | {\rm Inv_M}( \alpha^2 + \alpha) = {\rm Inv_M}( \alpha^4) = \alpha^{-4} = \alpha^3 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Because of $\alpha^3 = \alpha + 1$ the <u>proposed solutions 2 and 3</u> are correct. | + | *Because of $\alpha^3 = \alpha + 1$ the <u>proposed solutions 2 and 3</u> are correct. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
[[Category:Channel Coding: Exercises|^2.2 Extension Field^]] | [[Category:Channel Coding: Exercises|^2.2 Extension Field^]] | ||
Latest revision as of 12:48, 4 October 2022
We consider the extension field with eight elements ⇒ $\rm GF(2^3)$ according to the adjacent table. Since the underlying polynomial
- $$p(x) = x^3 + x +1 $$
is both, irreducible and primitive, the Galois field can be stated in the following form:
- $${\rm GF}(2^3) = \{\hspace{0.1cm}0\hspace{0.05cm},\hspace{0.1cm} 1,\hspace{0.05cm}\hspace{0.1cm} \alpha\hspace{0.05cm},\hspace{0.1cm} \alpha^{2}\hspace{0.05cm},\hspace{0.1cm} \alpha^{3}\hspace{0.05cm},\hspace{0.1cm} \alpha^{4}\hspace{0.05cm},\hspace{0.1cm} \alpha^{5}\hspace{0.05cm},\hspace{0.1cm} \alpha^{6}\hspace{0.1cm}\}\hspace{0.05cm}. $$
The element $\alpha$ results thereby as solution of the equation $p(\alpha) = 0$ in the Galois field $\rm GF(2)$.
- This gives the following constraint:
- $$\alpha^3 + \alpha +1 = 0\hspace{0.3cm} \Rightarrow\hspace{0.3cm} \alpha^3 = \alpha +1\hspace{0.05cm}.$$
- The following calculations apply to the other elements:
- $$\alpha^4 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^3 = \alpha \cdot (\alpha + 1) = \alpha^2 + \alpha \hspace{0.05cm},$$
- $$\alpha^5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^4 = \alpha \cdot (\alpha^2 +\alpha) = \alpha^3 + \alpha^2 = \alpha^2 + \alpha + 1\hspace{0.05cm},$$
- $$\alpha^6 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^5 = \alpha \cdot (\alpha^2 +\alpha + 1)= \alpha^3 + \alpha^2 + \alpha= \alpha + 1 + \alpha^2 + \alpha = \alpha^2+ 1\hspace{0.05cm}.$$
In this exercise you are to do some algebraic transformations in the Galois field $\rm GF(2^3)$.
- Among other things you are asked for the multiplicative inverse of the element $\alpha^4$.
- Then it must hold:
- $$\alpha^4 \cdot {\rm Inv_M}( \alpha^4) = 1 \hspace{0.05cm}.$$
Hints:
- This exercise belongs to the chapter "Extension Field".
- This exercise is intended as a supplement to the slightly more difficult "Exercise 2.5".
Questions
Solution
- $$\alpha^7 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^6 = \alpha \cdot (\alpha^2 + 1) = \alpha^3 + \alpha = (\alpha + 1) + \alpha = 1 \hspace{0.05cm},$$
- $$\alpha^8 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^7 = \alpha \cdot 1 = \alpha\hspace{0.05cm},$$
- $$\alpha^{13} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^7 \cdot \alpha^6 = 1 \cdot \alpha^6 = \alpha^2 + 1\hspace{0.05cm}.$$
- The table can therefore be continued modulo $7$.
- This means: All proposed solutions are correct.
(2) Correct is the proposed solution 2 because of
- $\alpha^8 = \alpha$ according to subtask (1),
- $\alpha^6 = \alpha^2 + 1$ $($according to the table$)$, and
- $-\alpha^2 = \alpha^2$ $($operations in the binary Galois field$)$.
So applies:
- $$A = \alpha^8 + \alpha^6 - \alpha^2 + 1 = \alpha + (\alpha^2 + 1) + \alpha^2 + 1 = \alpha \hspace{0.05cm}.$$
(3) With $\alpha^{16} = \alpha^{16-14} = \alpha^2$ and $\alpha^{12} \cdot \alpha^3 = \alpha^{15} = \alpha^{15-14} = \alpha$ we obtain the proposed solution 5:
- $$B = \alpha^2 + \alpha= \alpha^4 \hspace{0.05cm}.$$
(4) It holds $\alpha^3 = \alpha + 1$ ⇒ $C = \alpha^3 + \alpha = \alpha + 1 + \alpha = 1$ ⇒ Proposed solution 1.
(5) With $\alpha^4 = \alpha^2 + \alpha$ we obtain $D = \alpha^4 + \alpha = \alpha^2$ ⇒ Proposed solution 3.
(6) Correct is the proposed solution 4:
- $$E = A \cdot B \cdot C/D = \alpha \cdot \alpha^4 \cdot 1/\alpha^2 = \alpha^3 \hspace{0.05cm}.$$
(7) According to the table, $\alpha^2 + \alpha = \alpha^4$ holds. Therefore must be valid:
- $$\alpha^4 \cdot {\rm Inv_M}( \alpha^4) = 1 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} {\rm Inv_M}( \alpha^2 + \alpha) = {\rm Inv_M}( \alpha^4) = \alpha^{-4} = \alpha^3 \hspace{0.05cm}.$$
- Because of $\alpha^3 = \alpha + 1$ the proposed solutions 2 and 3 are correct.