Difference between revisions of "Aufgaben:Exercise 2.5: Three Variants of GF(2 power 4)"
| Line 60: | Line 60: | ||
p(x) = x^4 + x +1 =p_1(x)\hspace{0.05cm}.$$ | p(x) = x^4 + x +1 =p_1(x)\hspace{0.05cm}.$$ | ||
| − | Thus, the <u>proposed solution 1</u> is correct. | + | Thus, the <u>proposed solution 1</u> is correct. |
| + | '''(2)''' Following the same procedure, it can be shown that the power table $\rm (B)$ is based on the polynomial $p_2(x) = x^4 + x^3 + 1$ ⇒ <u>Proposed solution 2</u>. | ||
| − | |||
| + | '''(3)''' Starting from polynomial $p_2(x) = x^4 + x^3 + 1$ one obtains from the determining equation $p(\alpha) = 0$ the result $\alpha^4 = \alpha^3 + 1$. This further yields: | ||
| + | :$$\alpha^5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^4 = \alpha \cdot (\alpha^3 + 1) = \alpha^4 + \alpha = \alpha^3 + \alpha +1\hspace{0.05cm} \Rightarrow\hspace{0.05cm}{\rm vector\hspace{0.15cm} 1011},$$ | ||
| + | :$$\alpha^6 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^5 = \alpha \cdot (\alpha^3 +\alpha + 1) = \alpha^4 + \alpha^2 + \alpha= \alpha^3 +\alpha^2 + \alpha + 1\hspace{0.05cm} \Rightarrow\hspace{0.05cm}{\rm vector\hspace{0.15cm} 1111},$$ | ||
| + | :$$\alpha^7 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^6 = \alpha^4 +\alpha^3 +\alpha^2 +\alpha = \alpha^2 + \alpha + 1\hspace{0.05cm} \Rightarrow\hspace{0.05cm}{\rm vector\hspace{0.15cm} 0111},$$ | ||
| + | :$$\alpha^8 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^7 = \alpha \cdot (\alpha^2 + \alpha + 1) = \alpha^3 +\alpha^2 +\alpha \hspace{0.05cm} \Rightarrow\hspace{0.05cm}{\rm vector\hspace{0.15cm} 1110}.$$ | ||
| + | *Thus, only the <u>proposed solutions 1 and 4</u> are correct. The other two statements are interchanged. | ||
| + | |||
| + | *The following are the complete power tables for $p_1(x) = x^4 + x + 1$ (left, red background) and for $p_2(x) = x^4 + x^3 + 1$ (right, blue background). | ||
| − | + | [[File:P_ID2512__KC_A_2_5d_neu.png|right|frame|Complete power tables over $\rm GF(2^4)$ for two different polynomials <br>$($Sorry, we used here the German terms$)$]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''(4)''' The polynomials $p_1(x) = x^4 + x + 1$ and $p_2(x) = x^4 + x^3 + 1$ are primitive. | |
| − | + | *This can be seen from the fact that $\alpha^i \ne 1$ for $0 < i < 14$ in each case. | |
| − | + | ||
| − | '''(4)''' | + | *In contrast, $\alpha^{15} = \alpha^0 = 1$ holds. In both cases, the Galois field can be expressed as follows: |
| − | *This can be seen from the fact that $\alpha^i | ||
| − | *In contrast, $\alpha^{15} = \alpha^0 = 1$ holds. In both cases, the Galois field can be expressed as follows: | ||
:$${\rm GF}(2^4) = \{\hspace{0.1cm}0\hspace{0.05cm},\hspace{0.1cm} \alpha^{0} = 1,\hspace{0.05cm}\hspace{0.1cm} | :$${\rm GF}(2^4) = \{\hspace{0.1cm}0\hspace{0.05cm},\hspace{0.1cm} \alpha^{0} = 1,\hspace{0.05cm}\hspace{0.1cm} | ||
\alpha\hspace{0.05cm},\hspace{0.1cm} \alpha^{2},\hspace{0.1cm} ... \hspace{0.1cm} , \hspace{0.1cm}\alpha^{14}\hspace{0.1cm}\}\hspace{0.05cm}. $$ | \alpha\hspace{0.05cm},\hspace{0.1cm} \alpha^{2},\hspace{0.1cm} ... \hspace{0.1cm} , \hspace{0.1cm}\alpha^{14}\hspace{0.1cm}\}\hspace{0.05cm}. $$ | ||
| − | For the polynomial $p_3(x) = x^4 + x^3 + x^2 + x +1$ we get: | + | ⇒ For the polynomial $p_3(x) = x^4 + x^3 + x^2 + x +1$ we get: |
| − | :$$\alpha^4 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^3 + \alpha^2 + \alpha +1\hspace{0.25cm} \Rightarrow\hspace{0.25cm}{\rm | + | :$$\alpha^4 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^3 + \alpha^2 + \alpha +1\hspace{0.25cm} \Rightarrow\hspace{0.25cm}{\rm vector\hspace{0.15cm} 1111}\hspace{0.05cm},$$ |
| − | :$$\alpha^5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^4 = \alpha^4 + \alpha^3 + \alpha^2 + \alpha = (\alpha^3 + \alpha^2 + \alpha +1) + \alpha^3 + \alpha^2 + \alpha = 1 \hspace{0.25cm} \Rightarrow\hspace{0.25cm}{\rm | + | :$$\alpha^5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^4 = \alpha^4 + \alpha^3 + \alpha^2 + \alpha = $$ |
| − | + | ::$$= (\alpha^3 + \alpha^2 + \alpha +1) + \alpha^3 + \alpha^2 + \alpha = 1 \hspace{0.25cm} \Rightarrow\hspace{0.25cm}{\rm vector\hspace{0.15cm} 0001}\hspace{0.05cm}.$$ | |
| − | *So here already $\alpha^5 = \alpha^0 = 1 \Rightarrow \ p_3(x)$ is not a primitive polynomial ⇒ <u>Proposed solution 2</u>. | + | *So here is already $\alpha^5 = \alpha^0 = 1 $ <br>$\Rightarrow \ p_3(x)$ is not a primitive polynomial ⇒ <u>Proposed solution 2</u>. |
| − | *For the other powers | + | |
| + | *For the other powers of this polynomial holds: | ||
:$$\alpha^6 = \alpha^{11} = \alpha\hspace{0.05cm},\hspace{0.2cm} | :$$\alpha^6 = \alpha^{11} = \alpha\hspace{0.05cm},\hspace{0.2cm} | ||
\alpha^7 = \alpha^{12} = \alpha^2\hspace{0.05cm},\hspace{0.2cm} | \alpha^7 = \alpha^{12} = \alpha^2\hspace{0.05cm},\hspace{0.2cm} | ||
Latest revision as of 18:10, 3 October 2022
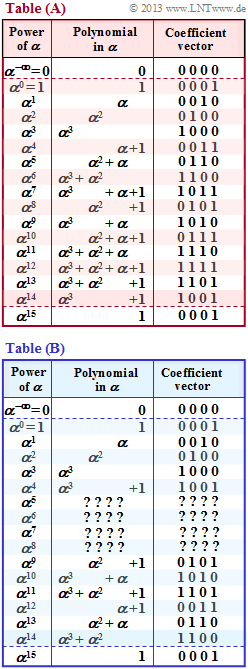
Irreducible and primitive polynomials have great importance in the description of error correction methods. For example, in [LN97] one finds the following irreducible polynomials of degree $m = 4$:
- $p_1(x) = x^4 + x +1$,
- $p_2(x) = x^4 + x^3 + 1$,
- $p_3(x) = x^4 + x^3 + x^2 + x + 1$.
The first two polynomials are also primitive. This can be seen from the power tables given on the right – the lower table $\rm (B)$ however not quite complete.
- From both tables we see that all powers $\alpha^i$ for $1 ≤ i ≤ 14$ are unequal $1$ in the polynomial representation. Only for $i = 15$ it follows that
- $$\alpha^{15} = \alpha^{0} = 1 \hspace{0.3cm} \Rightarrow\hspace{0.3cm}{\rm Coefficient\hspace{0.15cm}vector\hspace{0.15cm} 0001}\hspace{0.05cm} .$$
- It is not specified whether the tables $\rm (A)$ and $\rm (B)$ result from the polynomial $p_1(x) = x^4 + x + 1$ or from $p_2(x) =x^4 + x^3 + 1$. You are to make these assignments in subtasks (1) and (2).
- In the subtask (3) you are also to complete the missing powers $\alpha^5, \ \alpha^6, \ \alpha^7$ and $\alpha^8$ in the table $\rm (B)$.
- The subtask (4) refers to the also irreducible polynomial $p_3(x) = x^4 + x^3 + x^2 + x +1$. According to the above criteria, you are to decide whether this polynomial is primitive.
Hints:
- The exercise belongs to the chapter "Extension Field".
- The literature citation [LN97] refers to the book "Lidl, R.; Niederreiter, H.: Finite Fields. Encyclopedia of Mathematics and its Application. 2nd ed. Cambridge: University Press, 1997."
Questions
Solution
- $$\alpha^{4} = \alpha + 1 \hspace{0.3cm} \Rightarrow\hspace{0.3cm}\alpha^{4} + \alpha + 1 = 0 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} p(x) = x^4 + x +1 =p_1(x)\hspace{0.05cm}.$$
Thus, the proposed solution 1 is correct.
(2) Following the same procedure, it can be shown that the power table $\rm (B)$ is based on the polynomial $p_2(x) = x^4 + x^3 + 1$ ⇒ Proposed solution 2.
(3) Starting from polynomial $p_2(x) = x^4 + x^3 + 1$ one obtains from the determining equation $p(\alpha) = 0$ the result $\alpha^4 = \alpha^3 + 1$. This further yields:
- $$\alpha^5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^4 = \alpha \cdot (\alpha^3 + 1) = \alpha^4 + \alpha = \alpha^3 + \alpha +1\hspace{0.05cm} \Rightarrow\hspace{0.05cm}{\rm vector\hspace{0.15cm} 1011},$$
- $$\alpha^6 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^5 = \alpha \cdot (\alpha^3 +\alpha + 1) = \alpha^4 + \alpha^2 + \alpha= \alpha^3 +\alpha^2 + \alpha + 1\hspace{0.05cm} \Rightarrow\hspace{0.05cm}{\rm vector\hspace{0.15cm} 1111},$$
- $$\alpha^7 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^6 = \alpha^4 +\alpha^3 +\alpha^2 +\alpha = \alpha^2 + \alpha + 1\hspace{0.05cm} \Rightarrow\hspace{0.05cm}{\rm vector\hspace{0.15cm} 0111},$$
- $$\alpha^8 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^7 = \alpha \cdot (\alpha^2 + \alpha + 1) = \alpha^3 +\alpha^2 +\alpha \hspace{0.05cm} \Rightarrow\hspace{0.05cm}{\rm vector\hspace{0.15cm} 1110}.$$
- Thus, only the proposed solutions 1 and 4 are correct. The other two statements are interchanged.
- The following are the complete power tables for $p_1(x) = x^4 + x + 1$ (left, red background) and for $p_2(x) = x^4 + x^3 + 1$ (right, blue background).
(4) The polynomials $p_1(x) = x^4 + x + 1$ and $p_2(x) = x^4 + x^3 + 1$ are primitive.
- This can be seen from the fact that $\alpha^i \ne 1$ for $0 < i < 14$ in each case.
- In contrast, $\alpha^{15} = \alpha^0 = 1$ holds. In both cases, the Galois field can be expressed as follows:
- $${\rm GF}(2^4) = \{\hspace{0.1cm}0\hspace{0.05cm},\hspace{0.1cm} \alpha^{0} = 1,\hspace{0.05cm}\hspace{0.1cm} \alpha\hspace{0.05cm},\hspace{0.1cm} \alpha^{2},\hspace{0.1cm} ... \hspace{0.1cm} , \hspace{0.1cm}\alpha^{14}\hspace{0.1cm}\}\hspace{0.05cm}. $$
⇒ For the polynomial $p_3(x) = x^4 + x^3 + x^2 + x +1$ we get:
- $$\alpha^4 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^3 + \alpha^2 + \alpha +1\hspace{0.25cm} \Rightarrow\hspace{0.25cm}{\rm vector\hspace{0.15cm} 1111}\hspace{0.05cm},$$
- $$\alpha^5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^4 = \alpha^4 + \alpha^3 + \alpha^2 + \alpha = $$
- $$= (\alpha^3 + \alpha^2 + \alpha +1) + \alpha^3 + \alpha^2 + \alpha = 1 \hspace{0.25cm} \Rightarrow\hspace{0.25cm}{\rm vector\hspace{0.15cm} 0001}\hspace{0.05cm}.$$
- So here is already $\alpha^5 = \alpha^0 = 1 $
$\Rightarrow \ p_3(x)$ is not a primitive polynomial ⇒ Proposed solution 2.
- For the other powers of this polynomial holds:
- $$\alpha^6 = \alpha^{11} = \alpha\hspace{0.05cm},\hspace{0.2cm} \alpha^7 = \alpha^{12} = \alpha^2\hspace{0.05cm},\hspace{0.2cm} \alpha^8 = \alpha^{13} = \alpha^3\hspace{0.05cm},$$
- $$\alpha^9 = \alpha^{14} = \alpha^4\hspace{0.05cm},\hspace{0.2cm} \alpha^{10} = \alpha^{15} = \alpha^0 = 1\hspace{0.05cm}.$$