Difference between revisions of "Aufgaben:Exercise 3.13: Path Weighting Function again"
m (Guenter moved page Aufgabe 3.13: Nochmals zu den Pfadgewichtsfunktionen to Exercise 3.13: Path Weighting Function again) |
|||
| (9 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Distance_Characteristics_and_Error_Probability_Barriers}} |
| − | [[File: | + | [[File:EN_KC_A_3_13.png|right|frame|For the reduction of the state transition diagram]] |
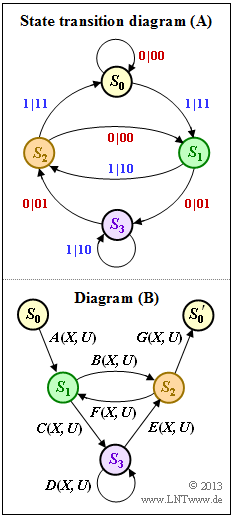
| − | + | In the [[Channel_Coding/Distance_Characteristics_and_Error_Probability_Barriers#Rules_for_manipulating_the_state_transition_diagram|"rules for manipulating the state transition diagram"]] section, for the example of our rate $1/2$ standard encoder | |
| − | + | *with memory $m = 2$ and | |
| − | + | *the transfer function matrix | |
| + | :$${\boldsymbol{\rm G}}(D) = \big ( 1 + D + D^2\hspace{0.05cm},\hspace{0.1cm} 1 + D^2 \hspace{0.05cm}\big ),$$ | ||
| + | |||
| + | the calculation of path weighting enumerator functions was described in great detail. The results given were: | ||
:$$T_{\rm enh}(X, U) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} \frac{U\hspace{-0.05cm} X^5}{1- 2U\hspace{-0.05cm}X} =U\hspace{-0.05cm}X^5 \cdot \big [ 1 + (2U\hspace{-0.08cm}X) + (2U\hspace{-0.08cm}X)^2 + \text{...} \hspace{0.05cm} \big ] \hspace{0.01cm},$$ | :$$T_{\rm enh}(X, U) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} \frac{U\hspace{-0.05cm} X^5}{1- 2U\hspace{-0.05cm}X} =U\hspace{-0.05cm}X^5 \cdot \big [ 1 + (2U\hspace{-0.08cm}X) + (2U\hspace{-0.08cm}X)^2 + \text{...} \hspace{0.05cm} \big ] \hspace{0.01cm},$$ | ||
:$$T(X) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} \frac{X^5}{1- 2X} = X^5 \cdot \big [ 1 + (2X) + (2X)^2 + \text{...} \hspace{0.05cm} \big ] \hspace{0.05cm}.$$ | :$$T(X) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} \frac{X^5}{1- 2X} = X^5 \cdot \big [ 1 + (2X) + (2X)^2 + \text{...} \hspace{0.05cm} \big ] \hspace{0.05cm}.$$ | ||
| − | + | Now the same calculations shall be done for the [[Channel_Coding/Algebraic_and_Polynomial_Description#Systematic_convolutional_codes|"equivalent systematic encoder"]] with the transfer function matrix | |
| − | :$${\boldsymbol{\rm G}}(D) = \big ( 1 \hspace{0.05cm},\hspace{0.1cm} (1 | + | :$${\boldsymbol{\rm G}}(D) = \big ( 1 \hspace{0.05cm},\hspace{0.1cm} (1 + D^2)/(1 + D + D^2) \hspace{0.05cm}\big ).$$ |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | *The diagram shows the state transition diagram $\rm (A)$ and the structure of the reduced diagram $\rm (B)$, where the transitions are denoted by $A(X, \, U), \ \text{...}\ , \ G(X, \, U)$ in general. | ||
| + | |||
| + | *In subtask '''(1)''' these abbreviations are to be adapted to the state transition diagram $\rm (A)$ . | ||
| + | Hints: | ||
| + | * This exercise belongs to the chapter [[Channel_Coding/Distance_Characteristics_and_Error_Probability_Bounds| "Distance Characteristics and Error Probability Bounds"]]. | ||
| + | |||
| + | * For the solution of subtasks '''(2)''' and '''(3)''' we refer here again to the section [[Channel_Coding/Distance_Characteristics_and_Error_Probability_Bounds#Rules_for_manipulating_the_state_transition_diagram|"Rules for manipulating the state transition diagram"]] in the theory part. | ||
| − | + | ===Questions=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What expressions do the following abbreviations stand for? |
|type="[]"} | |type="[]"} | ||
+ $A(X, \, U) = UX^2$, | + $A(X, \, U) = UX^2$, | ||
| Line 43: | Line 41: | ||
+ $G(X, \, U) = UX^2$. | + $G(X, \, U) = UX^2$. | ||
| − | { | + | {What expressions apply to the extended path weighting enumerator function? |
|type="[]"} | |type="[]"} | ||
- $T_{\rm enh}(X, \, U) = UX^5 \ / \ (1 \, –2UX)$. | - $T_{\rm enh}(X, \, U) = UX^5 \ / \ (1 \, –2UX)$. | ||
- $T_{\rm enh}(X, \, U) = UX^5 + 2 U^2X^6 + 4U^3X^7 + 8U^4X^8 + \ \text{...}$, | - $T_{\rm enh}(X, \, U) = UX^5 + 2 U^2X^6 + 4U^3X^7 + 8U^4X^8 + \ \text{...}$, | ||
| − | + | + | + None of the proposals are correct. |
| − | { | + | {What expressions apply to the "simple path weighting enumerator function"? |
|type="[]"} | |type="[]"} | ||
+ $T(X) = X^5 \ / \ (1 \, –2X)$. | + $T(X) = X^5 \ / \ (1 \, –2X)$. | ||
+ $T(X) = X^5 + 2X^6 + 4X^7 + 8X^8 + \ \text{...} $ | + $T(X) = X^5 + 2X^6 + 4X^7 + 8X^8 + \ \text{...} $ | ||
| − | - | + | - None of the proposals are correct. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' <u> | + | '''(1)''' <u>All proposed solutions</u> are correct. In the adapted diagram $\rm (B)$ all transitions are drawn: |
| − | [[File: | + | [[File:EN_KC_A_3_13a.png|right|frame|Reduction of the state transition diagram]] |
| − | * | + | *The transition from $S_0$ to $S_1$ is denoted by "$1 \ | \ 11$". |
| − | * | + | |
| − | * | + | *The output sequence $\underline{x}_i = (11)$ is expressed by $X^2$, the input bit $u_i = 1$ by $U$. |
| + | |||
| + | *The same result is obtained for $G(X, \, U)$: | ||
:$$A(X, U) = G(X, U)= UX^2 | :$$A(X, U) = G(X, U)= UX^2 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *The output sequences $\underline{x}_i = (01)$ as well as $\underline{x}_i = (10)$ are both marked with $X$. |
| − | * | + | |
| + | *Taking into account the input bits, we thus obtain: | ||
:$$u_i = 1\hspace{-0.1cm}:\hspace{0.15cm} B(X, U) = D(X, U)= UX\hspace{0.05cm},$$ | :$$u_i = 1\hspace{-0.1cm}:\hspace{0.15cm} B(X, U) = D(X, U)= UX\hspace{0.05cm},$$ | ||
:$$u_i = 0\hspace{-0.1cm}:\hspace{0.15cm} C(X, U) = E(X, U)= X | :$$u_i = 0\hspace{-0.1cm}:\hspace{0.15cm} C(X, U) = E(X, U)= X | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *The transition "$0 \ | \ 00$" from $S_2$ to $S_1$ is expressed by $F(X, \, U) = 1$. |
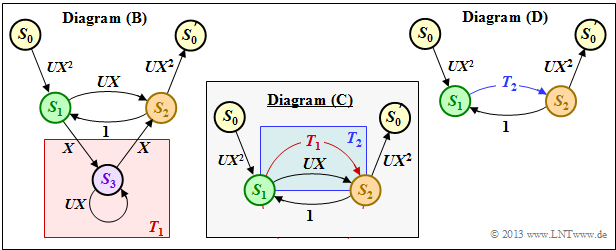
| − | '''(2)''' | + | '''(2)''' According to the method in section [[Channel_Coding/Distance_Characteristics_and_Error_Probability_Barriers#Rules_for_manipulating_the_state_transition_diagram|"Rules for manipulating the state transition diagram"]] in the theory part, first the transition from $S_1$ to $S_2$ via $S_3$ is summarized by an "ring". |
| − | * | + | |
| + | * One obtains for the red background in the diagram $\rm (B)$: | ||
:$$T_1(X, U) = \frac{A(X, U) \cdot B(X, U)}{1- C(X, U)} = \frac{X \cdot X}{1- U \cdot X} | :$$T_1(X, U) = \frac{A(X, U) \cdot B(X, U)}{1- C(X, U)} = \frac{X \cdot X}{1- U \cdot X} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | * The two "parallel transitions" corresponding to the blue background in the diagram $\rm (C)$ can be combined as follows: |
:$$T_2(X, U) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} T_1(X, U) + B(X, U) =\frac{X^2}{1- U X}+ U X = | :$$T_2(X, U) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} T_1(X, U) + B(X, U) =\frac{X^2}{1- U X}+ U X = | ||
\frac{X^2 + U- U^2X^2}{1- U X} | \frac{X^2 + U- U^2X^2}{1- U X} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | * The extended path weighting enumerator function results according to diagram $\rm (D)$ as "feedback<": |
:$$T_{\rm enh}(X, U) = \frac{A(X, U) \cdot G(X, U)\cdot T_2(X, U)}{1- F(X, U) \cdot T_2(X, U)} | :$$T_{\rm enh}(X, U) = \frac{A(X, U) \cdot G(X, U)\cdot T_2(X, U)}{1- F(X, U) \cdot T_2(X, U)} | ||
= \frac{UX^2 \cdot UX^2\cdot \frac{X^2 + UX- U^2X^2}{1- U X}}{1- 1 \cdot \frac{X^2 + UX- U^2X^2}{1- U X}}\hspace{0.05cm}.$$ | = \frac{UX^2 \cdot UX^2\cdot \frac{X^2 + UX- U^2X^2}{1- U X}}{1- 1 \cdot \frac{X^2 + UX- U^2X^2}{1- U X}}\hspace{0.05cm}.$$ | ||
| − | + | Even after several attempts, the author has not succeeded in further simplifying this expression in a target-oriented way. He tends to the <u>proposed solution 3</u> with the addition "without guarantee". | |
| − | * | + | |
| − | + | *However, this result would imply that the extended path weighting enumerator function of the equivalent systematic code is different from that of the nonsystematic code. We will still clarify this issue with an expert. | |
| − | '''(3)''' | + | |
| − | * | + | '''(3)''' Correct are the <u>proposed solutions 1 and 2</u>: |
| + | *If one sets the formal parameter $U = 1$ in the extended function $T_{\rm enh}(X, \, U)$, one obtains the solution proposition 1: | ||
:$$T(X) = \frac{X^4 \cdot \frac{X^2 + X- X^2}{1- X}}{1- \frac{X^2 + X- X^2}{1- X}}= | :$$T(X) = \frac{X^4 \cdot \frac{X^2 + X- X^2}{1- X}}{1- \frac{X^2 + X- X^2}{1- X}}= | ||
\frac{X^5 }{1- X - X} = | \frac{X^5 }{1- X - X} = | ||
\frac{X^5 }{1- 2X} \hspace{0.05cm}.$$ | \frac{X^5 }{1- 2X} \hspace{0.05cm}.$$ | ||
| − | * | + | *Using the series expansion $1/(1 \, –x) = 1 + x + x^2 + \ \text{...}\ $, we arrive at the proposed solution 2. |
| − | * | + | |
| + | *That is, the simple path weighting enumerator function $T(X)$ matches for both codes. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category:Channel Coding: Exercises|^3.5 | + | [[Category:Channel Coding: Exercises|^3.5 Distance Properties^]] |
Latest revision as of 17:50, 22 November 2022
In the "rules for manipulating the state transition diagram" section, for the example of our rate $1/2$ standard encoder
- with memory $m = 2$ and
- the transfer function matrix
- $${\boldsymbol{\rm G}}(D) = \big ( 1 + D + D^2\hspace{0.05cm},\hspace{0.1cm} 1 + D^2 \hspace{0.05cm}\big ),$$
the calculation of path weighting enumerator functions was described in great detail. The results given were:
- $$T_{\rm enh}(X, U) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} \frac{U\hspace{-0.05cm} X^5}{1- 2U\hspace{-0.05cm}X} =U\hspace{-0.05cm}X^5 \cdot \big [ 1 + (2U\hspace{-0.08cm}X) + (2U\hspace{-0.08cm}X)^2 + \text{...} \hspace{0.05cm} \big ] \hspace{0.01cm},$$
- $$T(X) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} \frac{X^5}{1- 2X} = X^5 \cdot \big [ 1 + (2X) + (2X)^2 + \text{...} \hspace{0.05cm} \big ] \hspace{0.05cm}.$$
Now the same calculations shall be done for the "equivalent systematic encoder" with the transfer function matrix
- $${\boldsymbol{\rm G}}(D) = \big ( 1 \hspace{0.05cm},\hspace{0.1cm} (1 + D^2)/(1 + D + D^2) \hspace{0.05cm}\big ).$$
- The diagram shows the state transition diagram $\rm (A)$ and the structure of the reduced diagram $\rm (B)$, where the transitions are denoted by $A(X, \, U), \ \text{...}\ , \ G(X, \, U)$ in general.
- In subtask (1) these abbreviations are to be adapted to the state transition diagram $\rm (A)$ .
Hints:
- This exercise belongs to the chapter "Distance Characteristics and Error Probability Bounds".
- For the solution of subtasks (2) and (3) we refer here again to the section "Rules for manipulating the state transition diagram" in the theory part.
Questions
Solution
- The transition from $S_0$ to $S_1$ is denoted by "$1 \ | \ 11$".
- The output sequence $\underline{x}_i = (11)$ is expressed by $X^2$, the input bit $u_i = 1$ by $U$.
- The same result is obtained for $G(X, \, U)$:
- $$A(X, U) = G(X, U)= UX^2 \hspace{0.05cm}.$$
- The output sequences $\underline{x}_i = (01)$ as well as $\underline{x}_i = (10)$ are both marked with $X$.
- Taking into account the input bits, we thus obtain:
- $$u_i = 1\hspace{-0.1cm}:\hspace{0.15cm} B(X, U) = D(X, U)= UX\hspace{0.05cm},$$
- $$u_i = 0\hspace{-0.1cm}:\hspace{0.15cm} C(X, U) = E(X, U)= X \hspace{0.05cm}.$$
- The transition "$0 \ | \ 00$" from $S_2$ to $S_1$ is expressed by $F(X, \, U) = 1$.
(2) According to the method in section "Rules for manipulating the state transition diagram" in the theory part, first the transition from $S_1$ to $S_2$ via $S_3$ is summarized by an "ring".
- One obtains for the red background in the diagram $\rm (B)$:
- $$T_1(X, U) = \frac{A(X, U) \cdot B(X, U)}{1- C(X, U)} = \frac{X \cdot X}{1- U \cdot X} \hspace{0.05cm}.$$
- The two "parallel transitions" corresponding to the blue background in the diagram $\rm (C)$ can be combined as follows:
- $$T_2(X, U) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} T_1(X, U) + B(X, U) =\frac{X^2}{1- U X}+ U X = \frac{X^2 + U- U^2X^2}{1- U X} \hspace{0.05cm}.$$
- The extended path weighting enumerator function results according to diagram $\rm (D)$ as "feedback<":
- $$T_{\rm enh}(X, U) = \frac{A(X, U) \cdot G(X, U)\cdot T_2(X, U)}{1- F(X, U) \cdot T_2(X, U)} = \frac{UX^2 \cdot UX^2\cdot \frac{X^2 + UX- U^2X^2}{1- U X}}{1- 1 \cdot \frac{X^2 + UX- U^2X^2}{1- U X}}\hspace{0.05cm}.$$
Even after several attempts, the author has not succeeded in further simplifying this expression in a target-oriented way. He tends to the proposed solution 3 with the addition "without guarantee".
- However, this result would imply that the extended path weighting enumerator function of the equivalent systematic code is different from that of the nonsystematic code. We will still clarify this issue with an expert.
(3) Correct are the proposed solutions 1 and 2:
- If one sets the formal parameter $U = 1$ in the extended function $T_{\rm enh}(X, \, U)$, one obtains the solution proposition 1:
- $$T(X) = \frac{X^4 \cdot \frac{X^2 + X- X^2}{1- X}}{1- \frac{X^2 + X- X^2}{1- X}}= \frac{X^5 }{1- X - X} = \frac{X^5 }{1- 2X} \hspace{0.05cm}.$$
- Using the series expansion $1/(1 \, –x) = 1 + x + x^2 + \ \text{...}\ $, we arrive at the proposed solution 2.
- That is, the simple path weighting enumerator function $T(X)$ matches for both codes.