Difference between revisions of "Aufgaben:Exercise 3.11: Viterbi Path Finding"
| (2 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
[[File:P_ID2694__KC_A_3_11.png|right|frame|Evaluated trellis diagram]] | [[File:P_ID2694__KC_A_3_11.png|right|frame|Evaluated trellis diagram]] | ||
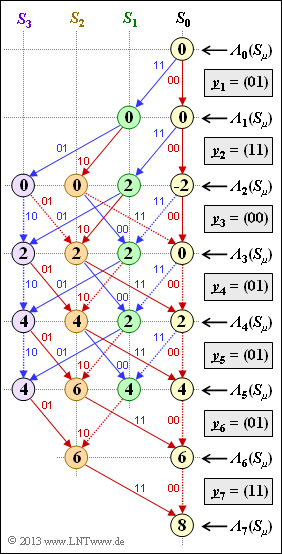
| − | One result of [[Aufgaben:Exercise_3.10:_Metric_Calculation| | + | One result of [[Aufgaben:Exercise_3.10:_Metric_Calculation| $\text{Exercise 3.10}$]] was adjacent trellis evaluation in terms of metrics ${\it \Lambda}_i(S_{\mu})$. |
| + | *At all decoding steps $i$ the $($in general$)$ $2^m = 4$ metrics were determined, selecting for each node the larger of two comparison values. | ||
| − | + | *The branch with the lower value was discarded. One can recognize discarded branches in the graph by dotted lines. | |
| − | |||
| − | At the end time (in the example $i = 7$ | + | Otherwise, the same conditions apply as for [[Aufgaben:Exercise_3.10:_Metric_Calculation| $\text{Exercise 3.10}$]]. For example, also in the adjacent graph, a red arrow indicates the information bit $u_i = 0$ and a blue arrow stands for $u_i = 1$. |
| − | * the | + | |
| + | In the present exercise we consider the second and important part of the Viterbi algorithm, namely the search for the "surviving paths" ${\it \Phi}_i(S_{\mu})$. These are at time $i$ in state $S_{\mu}$ with $\mu \in \{1,\ 2,\ 3,\ 4 \}$. The search is best organized in the backward direction $($i.e., from bottom to top in the graph$)$. | ||
| + | |||
| + | At the end time $($in the example $i = 7)$ there is only one surviving path ${\it \Phi}_7(S_0)$ due to termination. From this it is possible to extract: | ||
| + | * the sequence $\underline{z}$ selected by the decoder $($short: "decoder sequence"$)$ ⇒ highest possible probability ${\rm Pr}(\underline{z} = \underline{x})$, | ||
| + | |||
* the associated information sequence $\underline{v}$ with the greatest possible probability ${\rm Pr}(\underline{v} = \underline{u})$. | * the associated information sequence $\underline{v}$ with the greatest possible probability ${\rm Pr}(\underline{v} = \underline{u})$. | ||
| − | A decision at an earlier time, for example at $i = 5$, does not always satisfy the maximum likelihood criterion. Here there are four surviving paths ${\it \Phi}_5(S_0), \hspace{0.05cm}\text{ ...} \hspace{0.1cm} , \ {\it \Phi}_5(S_3)$, which at time $i = 5$ are in states $S_0, \hspace{0.05cm}\text{ ...} \hspace{0.1cm} , \ S_3$ | + | A decision at an earlier time, for example at $i = 5$, does not always satisfy the maximum likelihood criterion. Here there are four surviving paths ${\it \Phi}_5(S_0), \hspace{0.05cm}\text{ ...} \hspace{0.1cm} , \ {\it \Phi}_5(S_3)$, which at time $i = 5$ are in states $S_0, \hspace{0.05cm}\text{ ...} \hspace{0.1cm} , \ S_3$. |
| − | *One of these four paths is certainly part of the maximum likelihood path, which is the best possible path for $i → ∞$ $($at termination significantly earlier, here at $i = 7)$ | + | *One of these four paths is certainly part of the maximum likelihood path, which is the best possible path for $i → ∞$ $($at termination significantly earlier, here at $i = 7)$. |
| − | *But if a constraint decision is to be made already at time $i = 5$ one usually chooses the path ${\it \Phi}_5(S_{\mu})$ with the largest metric at that time ${\it \Lambda}_5(S_{\mu})$. | + | |
| + | *But if a constraint decision is to be made already at time $i = 5$, one usually chooses the path ${\it \Phi}_5(S_{\mu})$ with the largest metric at that time ${\it \Lambda}_5(S_{\mu})$. | ||
| Line 21: | Line 27: | ||
| − | Hints: | + | <u>Hints:</u> |
*This exercise belongs to the chapter [[Channel_Coding/Decoding_of_Convolutional_Codes| "Decoding of Convolutional Codes"]]. | *This exercise belongs to the chapter [[Channel_Coding/Decoding_of_Convolutional_Codes| "Decoding of Convolutional Codes"]]. | ||
| − | *Reference is made in particular to the | + | |
| + | *Reference is made in particular to the section [[Channel_Coding/Decoding_of_Convolutional_Codes#Evaluating_the_trellis_in_the_error-free_case_.E2.80.93_Path_search|"Evaluating the trellis in the error-free case – Path finding"]]. | ||
| Line 31: | Line 38: | ||
===Questions=== | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {For which | + | {For which estimated sequence $\underline{z}$ $($for the encoded sequence $\underline{z})$ does the decision fall at time $i = 7$? |
|type="()"} | |type="()"} | ||
- $\underline{z} = (11, \, 10, \, 00, \, 01, \, 01, \, 11, \, 00)$, | - $\underline{z} = (11, \, 10, \, 00, \, 01, \, 01, \, 11, \, 00)$, | ||
| Line 37: | Line 44: | ||
- $\underline{z} = (00, \, 11, \, 01, \, 01, \, 00, \, 10, \, 11)$. | - $\underline{z} = (00, \, 11, \, 01, \, 01, \, 00, \, 10, \, 11)$. | ||
| − | {How many transmission errors (at least) | + | {How many transmission errors have occurred $($at least$)$? |
|type="{}"} | |type="{}"} | ||
| − | $N_{\rm | + | $N_{\rm bit\:error} \ = \ ${ 3 3% } |
{Which information sequence $\underline{v}$ does the Viterbi decoder choose? | {Which information sequence $\underline{v}$ does the Viterbi decoder choose? | ||
| Line 47: | Line 54: | ||
- $\underline{v} = (0, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0)$. | - $\underline{v} = (0, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0)$. | ||
| − | {Would a final (and correct) decision have been possible already at $i = 6$ | + | {Would a final $($and correct$)$ decision have been possible already at $i = 6$? |
|type="()"} | |type="()"} | ||
- Yes. | - Yes. | ||
| Line 59: | Line 66: | ||
+ $S_0 → S_0 → S_1 → S_2 → S_1 → S_3$. | + $S_0 → S_0 → S_1 → S_2 → S_1 → S_3$. | ||
| − | {Which path would you choose at time $i = 5$ | + | {Which path would you choose at time $i = 5$? |
|type="()"} | |type="()"} | ||
- $S_0 → S_0 → S_1 → S_3 → S_2 → S_0$, | - $S_0 → S_0 → S_1 → S_3 → S_2 → S_0$, | ||
| Line 76: | Line 83: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
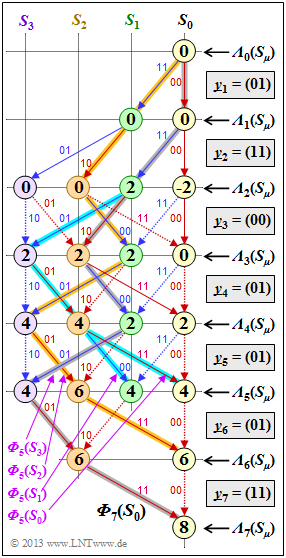
| − | '''(1)''' Correct is the <u>proposed solution 2</u>: | + | '''(1)''' Correct is the <u>proposed solution 2</u>: |
| − | *Unambiguously find the surviving path by searching backwards, i.e., from node ${\it \Lambda}_7(S_0)$ to node ${\it \Lambda}_0(S_0)$. | + | *Unambiguously find the surviving path by searching backwards, i.e., from node ${\it \Lambda}_7(S_0)$ to node ${\it \Lambda}_0(S_0)$. |
| − | *Using the | + | |
| + | *Using the 2-bit sequences $(00, \, 01, \, 10$ or $11)$ given at the transitions, we obtain in the forward direction the result according to <u>proposition 2</u>: | ||
:$$\underline{z} = \big (00\hspace{0.05cm}, 11\hspace{0.05cm}, 10\hspace{0.05cm}, 00\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 11\hspace{0.03cm} \big ) \hspace{0.05cm}.$$ | :$$\underline{z} = \big (00\hspace{0.05cm}, 11\hspace{0.05cm}, 10\hspace{0.05cm}, 00\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 11\hspace{0.03cm} \big ) \hspace{0.05cm}.$$ | ||
| − | * | + | *One not reach the final node ${\it \Lambda}_7(S_0)$ along other paths. |
| − | '''(2)''' By comparing the | + | '''(2)''' By comparing the decoder sequence $\underline{z}$ selected in subtask '''(1)''' with the received sequence |
| − | :$$\underline{y} = \big (01\hspace{0.05cm}, 11\hspace{0.05cm}, 00\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 11\hspace{0.03cm} \big )$$ | + | :$$\underline{y} = \big (01\hspace{0.05cm}, 11\hspace{0.05cm}, 00\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 11\hspace{0.03cm} \big ),$$ |
| − | one detects <u>three bit errors</u> at positions 2, 5, and 8. | + | one detects <u>three bit errors</u> at positions '''2''', '''5''', and '''8'''. |
| − | *If a | + | |
| − | *Because of the final value ${\it \Lambda}_7(S_0) = 8$ or ${\it \Gamma}_7(S_0) = 3$ – see [[Aufgaben:Exercise_3.10:_Metric_Calculation| | + | *If a encoded sequence $\underline{x} ≠ \underline{z}$ was sent, there can of course be more. |
| + | |||
| + | *Because of the final value ${\it \Lambda}_7(S_0) = 8$ or ${\it \Gamma}_7(S_0) = 3$ – see [[Aufgaben:Exercise_3.10:_Metric_Calculation|$\text{Exercise 3.10}$]] – but one can assume that a correct decision ⇒ $\underline{z} = \underline{x}$ has been made. | ||
[[File:P_ID2697__KC_A_3_11_ML_neu.png|right|frame|Viterbi path finding]] | [[File:P_ID2697__KC_A_3_11_ML_neu.png|right|frame|Viterbi path finding]] | ||
| − | '''(3)''' Correct is <u>proposed solution 1</u>: | + | '''(3)''' Correct is the <u>proposed solution 1</u>: |
| − | *From the colors of the surviving path – red represents $u_i = 0$ and blue represents $u_i = 1$ – one can see the correctness of <u>solution proposal 1</u>: red – blue – red – blue – blue – red – red. | + | *From the colors of the surviving path – red represents $u_i = 0$ and blue represents $u_i = 1$ – one can see the correctness of <u>solution proposal 1</u>: red – blue – red – blue – blue – red – red. |
| − | *It should be noted that the actual information sequence $\underline{u}$ is only of length $L = 5$. | + | |
| − | + | *It should be noted that the actual information sequence $\underline{u}$ is only of length $L = 5$. Only by termination one arrives at the total length $L' = L + m = 7$. | |
| + | |||
| + | '''(4)''' At time $i = 6$ there are still two surviving paths. | ||
| + | *A decision could be forcibly made based on the larger metric. | ||
| − | + | *However, because of ${\it \Lambda}_6(S_0) = {\it \Lambda}_6(S_2) = 6$ this is not possible in our example ⇒ <u>No</u>. | |
| − | '''(5)''' The graph shows that <u>all proposed solutions</u> are correct. The paths are labeled ${\it \Phi}_5(S_0)$, ... , ${\it \Phi}_5(S_3)$. | + | '''(5)''' The graph shows that <u>all proposed solutions</u> are correct. The paths are labeled ${\it \Phi}_5(S_0)$, ... , ${\it \Phi}_5(S_3)$. |
| − | '''(6)''' The constraint decision at time $i = 5$ would select the path with the largest metric ${\it \Lambda}_5(S_{\mu})$, i.e., the path ${\it \Phi}_5(S_2)$ corresponding to <u>proposition 3</u>. | + | '''(6)''' The constraint decision at time $i = 5$ would select the path with the largest metric ${\it \Lambda}_5(S_{\mu})$, <br>i.e., the path ${\it \Phi}_5(S_2)$ corresponding to <u>proposition 3</u>. |
| − | '''(7)''' Based on our solution to subtask (1), the path ${\it \Phi}_5(S_3)$ according to <u>proposition 4</u> would have been the better choice. | + | '''(7)''' Based on our solution to subtask '''(1)''', the path ${\it \Phi}_5(S_3)$ according to <u>proposition 4</u> would have been the better choice. This is part of the path to ${\it \Phi}_7(S_0)$. |
| − | + | ||
| − | *At | + | *At time $i = 5$, however, there is still nothing in favor of this choice. |
| − | *The (ultimately correct) path is only highlighted by the two termination bits. | + | |
| + | *The (ultimately correct) path is only highlighted by the two termination bits. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 16:06, 19 November 2022
One result of $\text{Exercise 3.10}$ was adjacent trellis evaluation in terms of metrics ${\it \Lambda}_i(S_{\mu})$.
- At all decoding steps $i$ the $($in general$)$ $2^m = 4$ metrics were determined, selecting for each node the larger of two comparison values.
- The branch with the lower value was discarded. One can recognize discarded branches in the graph by dotted lines.
Otherwise, the same conditions apply as for $\text{Exercise 3.10}$. For example, also in the adjacent graph, a red arrow indicates the information bit $u_i = 0$ and a blue arrow stands for $u_i = 1$.
In the present exercise we consider the second and important part of the Viterbi algorithm, namely the search for the "surviving paths" ${\it \Phi}_i(S_{\mu})$. These are at time $i$ in state $S_{\mu}$ with $\mu \in \{1,\ 2,\ 3,\ 4 \}$. The search is best organized in the backward direction $($i.e., from bottom to top in the graph$)$.
At the end time $($in the example $i = 7)$ there is only one surviving path ${\it \Phi}_7(S_0)$ due to termination. From this it is possible to extract:
- the sequence $\underline{z}$ selected by the decoder $($short: "decoder sequence"$)$ ⇒ highest possible probability ${\rm Pr}(\underline{z} = \underline{x})$,
- the associated information sequence $\underline{v}$ with the greatest possible probability ${\rm Pr}(\underline{v} = \underline{u})$.
A decision at an earlier time, for example at $i = 5$, does not always satisfy the maximum likelihood criterion. Here there are four surviving paths ${\it \Phi}_5(S_0), \hspace{0.05cm}\text{ ...} \hspace{0.1cm} , \ {\it \Phi}_5(S_3)$, which at time $i = 5$ are in states $S_0, \hspace{0.05cm}\text{ ...} \hspace{0.1cm} , \ S_3$.
- One of these four paths is certainly part of the maximum likelihood path, which is the best possible path for $i → ∞$ $($at termination significantly earlier, here at $i = 7)$.
- But if a constraint decision is to be made already at time $i = 5$, one usually chooses the path ${\it \Phi}_5(S_{\mu})$ with the largest metric at that time ${\it \Lambda}_5(S_{\mu})$.
Hints:
- This exercise belongs to the chapter "Decoding of Convolutional Codes".
- Reference is made in particular to the section "Evaluating the trellis in the error-free case – Path finding".
Questions
Solution
- Unambiguously find the surviving path by searching backwards, i.e., from node ${\it \Lambda}_7(S_0)$ to node ${\it \Lambda}_0(S_0)$.
- Using the 2-bit sequences $(00, \, 01, \, 10$ or $11)$ given at the transitions, we obtain in the forward direction the result according to proposition 2:
- $$\underline{z} = \big (00\hspace{0.05cm}, 11\hspace{0.05cm}, 10\hspace{0.05cm}, 00\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 11\hspace{0.03cm} \big ) \hspace{0.05cm}.$$
- One not reach the final node ${\it \Lambda}_7(S_0)$ along other paths.
(2) By comparing the decoder sequence $\underline{z}$ selected in subtask (1) with the received sequence
- $$\underline{y} = \big (01\hspace{0.05cm}, 11\hspace{0.05cm}, 00\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 11\hspace{0.03cm} \big ),$$
one detects three bit errors at positions 2, 5, and 8.
- If a encoded sequence $\underline{x} ≠ \underline{z}$ was sent, there can of course be more.
- Because of the final value ${\it \Lambda}_7(S_0) = 8$ or ${\it \Gamma}_7(S_0) = 3$ – see $\text{Exercise 3.10}$ – but one can assume that a correct decision ⇒ $\underline{z} = \underline{x}$ has been made.
(3) Correct is the proposed solution 1:
- From the colors of the surviving path – red represents $u_i = 0$ and blue represents $u_i = 1$ – one can see the correctness of solution proposal 1: red – blue – red – blue – blue – red – red.
- It should be noted that the actual information sequence $\underline{u}$ is only of length $L = 5$. Only by termination one arrives at the total length $L' = L + m = 7$.
(4) At time $i = 6$ there are still two surviving paths.
- A decision could be forcibly made based on the larger metric.
- However, because of ${\it \Lambda}_6(S_0) = {\it \Lambda}_6(S_2) = 6$ this is not possible in our example ⇒ No.
(5) The graph shows that all proposed solutions are correct. The paths are labeled ${\it \Phi}_5(S_0)$, ... , ${\it \Phi}_5(S_3)$.
(6) The constraint decision at time $i = 5$ would select the path with the largest metric ${\it \Lambda}_5(S_{\mu})$,
i.e., the path ${\it \Phi}_5(S_2)$ corresponding to proposition 3.
(7) Based on our solution to subtask (1), the path ${\it \Phi}_5(S_3)$ according to proposition 4 would have been the better choice. This is part of the path to ${\it \Phi}_7(S_0)$.
- At time $i = 5$, however, there is still nothing in favor of this choice.
- The (ultimately correct) path is only highlighted by the two termination bits.