Difference between revisions of "Aufgaben:Exercise 4.3: Iterative Decoding at the BSC"
| (7 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{quiz-Header|Buchseite=Channel_Coding/Soft-in_Soft-Out_Decoder}} | {{quiz-Header|Buchseite=Channel_Coding/Soft-in_Soft-Out_Decoder}} | ||
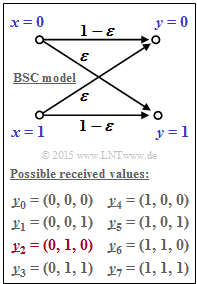
| − | [[File: | + | [[File:EN_KC_A_4_3.png|right|frame|BSC model and (above) <br>possible received values]] |
| − | We consider | + | We consider in this exercise two codes: |
| − | * the | + | * the "single parity–check code" ⇒ [[Channel_Coding/Examples_of_Binary_Block_Codes#Single_Parity-check_Codes| $\text{SPC (3, 2, 2)}$]]: |
:$$\underline{x} = \big (\hspace{0.05cm}(0, 0, 0), \hspace{0.1cm} | :$$\underline{x} = \big (\hspace{0.05cm}(0, 0, 0), \hspace{0.1cm} | ||
(0, 1, 1), \hspace{0.1cm} | (0, 1, 1), \hspace{0.1cm} | ||
| Line 9: | Line 9: | ||
(1, 1, 0) \hspace{0.05cm} \big ) | (1, 1, 0) \hspace{0.05cm} \big ) | ||
\hspace{0.05cm}, $$ | \hspace{0.05cm}, $$ | ||
| − | * the repetition code ⇒ [[Channel_Coding/Examples_of_Binary_Block_Codes#Repetition_Codes| $\text{ | + | * the repetition code ⇒ [[Channel_Coding/Examples_of_Binary_Block_Codes#Repetition_Codes| $\text{RC (3, 1, 3)}$]]: |
:$$\underline{x} = \big (\hspace{0.05cm}(0, 0, 0), \hspace{0.1cm} | :$$\underline{x} = \big (\hspace{0.05cm}(0, 0, 0), \hspace{0.1cm} | ||
(1, 1, 1) \hspace{0.05cm} \big ) | (1, 1, 1) \hspace{0.05cm} \big ) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| + | The channel is described at bit level by the [[Digital_Signal_Transmission/Binary_Symmetric_Channel|$\text{BSC model}$]]. According to the graphic, the following applies: | ||
| + | :$${\rm Pr}(y_i \ne x_i) =\varepsilon = 0.269\hspace{0.05cm},$$ | ||
| + | :$${\rm Pr}(y_i = x_i) =1-\varepsilon = 0.731\hspace{0.05cm}.$$ | ||
| − | + | Here, $\varepsilon$ denotes the falsification probability of the BSC model. | |
| − | |||
| − | |||
| − | + | Except for the last subtask, the following received value is always assumed: | |
| − | |||
| − | Except for the last subtask, the following received value is always assumed: | ||
:$$\underline{y} = (0, 1, 0) =\underline{y}_2 | :$$\underline{y} = (0, 1, 0) =\underline{y}_2 | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | The | + | The chosen indexing of all possible received vectors can be taken from the graphic. |
| − | *The most considered vector $\underline{y}_2$ is highlighted in red | + | *The most considered vector $\underline{y}_2$ is highlighted in red. |
| − | * | + | |
| + | *Only for subtask '''(6)''' applies: | ||
:$$\underline{y} = (1, 1, 0) =\underline{y}_6 | :$$\underline{y} = (1, 1, 0) =\underline{y}_6 | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
For decoding purposes, the exercise will examine: | For decoding purposes, the exercise will examine: | ||
| − | * the [[Channel_Coding/Decoding_of_Linear_Block_Codes#Generalization_of_syndrome_coding|" | + | * the [[Channel_Coding/Decoding_of_Linear_Block_Codes#Generalization_of_syndrome_coding|"syndrome decoding"]], which follows the concept "hard decision maximum likelihood detection" $\rm (HD-ML)$ for the codes under consideration. <br>$($because soft values are not available at the BSC$)$; |
| − | |||
| + | * the bit-wise [[Channel_Coding/Soft-in_Soft-Out_Decoder#Bit-wise_soft-in_soft-out_decoding|"Soft–in Soft–out Decoding"]] $\rm (SISO)$ according to this section. | ||
| Line 42: | Line 42: | ||
| + | <u>Hints:</u> | ||
| + | * This exercise refers to the chapter [[Channel_Coding/Soft-in_Soft-Out_Decoder| "Soft–in Soft–out Decoder"]]. | ||
| − | + | * Reference is made in particular to the sections | |
| − | + | :*[[Channel_Coding/Soft-in_Soft-Out_Decoder#Bit-wise_soft-in_soft-out_decoding|"Bit-wise Soft–in Soft–out Decoding"]], | |
| − | + | :*[[Channel_Coding/Channel_Models_and_Decision_Structures#Binary_Symmetric_Channel_.E2.80.93_BSC|"Binary Symmetric Channel"]] | |
| − | * Reference is made in particular to the | + | * The code word selected by the decoder is denoted in the questions by $\underline{z}$. |
| − | : | ||
| − | : | ||
| − | * The | ||
| Line 58: | Line 57: | ||
{Which statements are valid for decoding the $\text{SPC (3, 2, 2)}$? | {Which statements are valid for decoding the $\text{SPC (3, 2, 2)}$? | ||
|type="()"} | |type="()"} | ||
| − | - The | + | - The hard decision syndrome decoding yields the result $\underline{z} = (0, \, 1, \, 0)$. |
| − | - The | + | - The hard decision syndrome decoding returns the result $\underline{z} = (0, \, 0, \, 0)$. |
| − | + The | + | + The hard decision syndrome decoding fails here. |
{Which statements are valid for the $\text{ RC (3, 1, 3)}$? | {Which statements are valid for the $\text{ RC (3, 1, 3)}$? | ||
|type="()"} | |type="()"} | ||
| − | - The | + | - The hard decision syndrome decoding returns the result $\underline{z} = (0, \, 1, \, 0)$. |
| − | + The | + | + The hard decision syndrome decoding returns the result $\underline{z} = (0, \, 0, \, 0)$. |
| − | - The | + | - The hard decision syndrome decoding fails here. |
| − | {How certain is this decision if we define | + | {How certain is this decision if we define reliability $($"security"$)$ $S$ as the quotient of the probabilities for a correct or an incorrect decision? <br>Set the falsification probability of the BSC model to $\varepsilon = 26.9\%$. |
|type="{}"} | |type="{}"} | ||
$S \ = \ ${ 2.717 3% } | $S \ = \ ${ 2.717 3% } | ||
$\hspace{0.75cm} \ln {(S)} \ = \ ${ 1 3% } | $\hspace{0.75cm} \ln {(S)} \ = \ ${ 1 3% } | ||
| − | {What are the intrinsic | + | {What are the intrinsic log likelihood ratios for iterative bit-wise decoding of the $\text{RC (3, 1)}$ received word $\underline{y}_2 = (0, \, 1, \, 0)$? |
|type="{}"} | |type="{}"} | ||
$L_{\rm K}(1) \ = \ ${ 1 3% } | $L_{\rm K}(1) \ = \ ${ 1 3% } | ||
| Line 79: | Line 78: | ||
$L_{\rm K}(3) \ = \ ${ 1 3% } | $L_{\rm K}(3) \ = \ ${ 1 3% } | ||
| − | {Which statements are true for decoding the received word $\underline{y}_2 = (0, \, 1, \, 0)$ | + | {Which statements are true for decoding the received word $\underline{y}_2 = (0, \, 1, \, 0)$? Continue to assume the $\text{RC (3, 1, 3)}$. |
|type="[]"} | |type="[]"} | ||
+ From the first iteration all signs of $L_{\rm APP}(i)$ are positive. | + From the first iteration all signs of $L_{\rm APP}(i)$ are positive. | ||
+ Already after the second iteration ${\rm Pr}(\underline{x}_0\hspace{0.05cm} |\hspace{0.05cm} \underline{y}_2)$ is greater than $99\%$. | + Already after the second iteration ${\rm Pr}(\underline{x}_0\hspace{0.05cm} |\hspace{0.05cm} \underline{y}_2)$ is greater than $99\%$. | ||
| − | + With each iteration the absolute values $L_{\rm APP}(i)$ become larger. | + | + With each iteration the absolute values $|L_{\rm APP}(i)|$ become larger. |
| − | {Which statements are true for decoding the received word $\underline{y}_6 = (1, 1, 0)$ when $\underline{x}_0 = (0, 0, 0)$ was sent? | + | {Which statements are true for decoding the received word $\underline{y}_6 = (1, 1, 0)$, when $\underline{x}_0 = (0, 0, 0)$ was sent? |
|type="[]"} | |type="[]"} | ||
- The iterative decoder decides correctly. | - The iterative decoder decides correctly. | ||
+ The iterative decoder decides wrong. | + The iterative decoder decides wrong. | ||
| − | + The "reliability" for | + | + The "reliability" for $\underline{y}_6 \Rightarrow \underline{x}_0$ increases with increasing $I$. |
</quiz> | </quiz> | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Correct is the <u>proposed solution 3</u>: | + | '''(1)''' Correct is the <u>proposed solution 3</u>: |
| − | *The received word $\underline{y}_2 = (0, 1, 0)$ is not a valid | + | *The received word $\underline{y}_2 = (0, 1, 0)$ is not a valid code word of the single parity–check code $\text{SPC (3, 2)}$. Thus, the first statement is false. |
| − | |||
| + | *In addition, since the $\text{SPC (3, 2)}$ has only the minimum distance $d_{\rm min} = 2$, no error can be corrected. | ||
| − | '''(2)''' Correct is the <u>proposed solution 2</u>: | + | |
| − | *The possible | + | '''(2)''' Correct is the <u>proposed solution 2</u>: |
| − | *The minimum distance of this code is $d_{\rm min} = 3$, so $t = (d_{\rm min} \, - 1)/2 = 1$ error can be corrected. | + | *The possible code words at the $\text{RP (3, 1)}$ are $\underline{x}_0 = (0, 0, 0)$ and $\underline{x}_1 = (1, 1, 1)$. |
| − | *In addition to $\underline{y}_0 = (0, 0, 0)$, $\underline{y}_1 = (0, 0, 1), \ \underline{y}_2 = (0, 1, 0)$, and $\underline{y}_4 = (1, 0, 0)$ are also assigned to the decoding result $\underline{x}_0 = (0, 0, 0)$. | + | |
| + | *The minimum distance of this code is $d_{\rm min} = 3$, so $t = (d_{\rm min} \, - 1)/2 = 1$ error can be corrected. | ||
| + | |||
| + | *In addition to $\underline{y}_0 = (0, 0, 0)$, the received words $\underline{y}_1 = (0, 0, 1), \ \underline{y}_2 = (0, 1, 0)$, and $\underline{y}_4 = (1, 0, 0)$ are also assigned to the decoding result $\underline{x}_0 = (0, 0, 0)$. | ||
| − | '''(3)''' According to the BSC model, the conditional probability | + | '''(3)''' According to the BSC model, the conditional probability that $\underline{y}_2 = (0, 1, 0)$ is received, given that $\underline{x}_0 = (0, 0, 0)$ was sent: |
:$${\rm Pr}(\underline{y} = \underline{y}_2 \hspace{0.1cm}| \hspace{0.1cm}\underline{x} = \underline{x}_0 ) = (1-\varepsilon)^2 \cdot \varepsilon\hspace{0.05cm}.$$ | :$${\rm Pr}(\underline{y} = \underline{y}_2 \hspace{0.1cm}| \hspace{0.1cm}\underline{x} = \underline{x}_0 ) = (1-\varepsilon)^2 \cdot \varepsilon\hspace{0.05cm}.$$ | ||
| − | *The first term $(1 \, –\varepsilon)^2$ indicates the probability that the first and | + | *The first term $(1 \, –\varepsilon)^2$ indicates the probability that the first and third bit were transmitted correctly. $\varepsilon$ describes the falsification probability for the second bit. |
| − | *Correspondingly, for the second possible code word $\underline{x}_1 = (1, 1, 1)$: | + | *Correspondingly, for the second possible code word $\underline{x}_1 = (1, 1, 1)$: |
:$${\rm Pr}(\underline{y} = \underline{y}_2 \hspace{0.1cm}| \hspace{0.1cm}\underline{x} = \underline{x}_1 ) = \varepsilon^2 \cdot (1-\varepsilon) \hspace{0.05cm}.$$ | :$${\rm Pr}(\underline{y} = \underline{y}_2 \hspace{0.1cm}| \hspace{0.1cm}\underline{x} = \underline{x}_1 ) = \varepsilon^2 \cdot (1-\varepsilon) \hspace{0.05cm}.$$ | ||
| − | *According to Bayes' theorem, the inference probabilities are then: | + | *According to Bayes' theorem, the inference probabilities are then: |
:$${\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y} = \underline{y}_2 ) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Pr}(\underline{y} = \underline{y}_2 \hspace{0.1cm}| \hspace{0.1cm}\underline{x} = \underline{x}_0 ) \cdot \frac{{\rm Pr}(\underline{x} = \underline{x}_0)} | :$${\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y} = \underline{y}_2 ) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Pr}(\underline{y} = \underline{y}_2 \hspace{0.1cm}| \hspace{0.1cm}\underline{x} = \underline{x}_0 ) \cdot \frac{{\rm Pr}(\underline{x} = \underline{x}_0)} | ||
{{\rm Pr}(\underline{y} = \underline{y}_2)} \hspace{0.05cm},$$ | {{\rm Pr}(\underline{y} = \underline{y}_2)} \hspace{0.05cm},$$ | ||
:$${\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_1 \hspace{0.1cm}| \hspace{0.1cm}\underline{y} = \underline{y}_2 ) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Pr}(\underline{y} = \underline{y}_2 \hspace{0.1cm}| \hspace{0.1cm}\underline{x} = \underline{x}_1 ) \cdot \frac{{\rm Pr}(\underline{x} = \underline{x}_1)} | :$${\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_1 \hspace{0.1cm}| \hspace{0.1cm}\underline{y} = \underline{y}_2 ) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Pr}(\underline{y} = \underline{y}_2 \hspace{0.1cm}| \hspace{0.1cm}\underline{x} = \underline{x}_1 ) \cdot \frac{{\rm Pr}(\underline{x} = \underline{x}_1)} | ||
{{\rm Pr}(\underline{y} = \underline{y}_2)} $$ | {{\rm Pr}(\underline{y} = \underline{y}_2)} $$ | ||
| − | :$$\Rightarrow \hspace{0.3cm} S = \frac{{\rm Pr( | + | :$$\Rightarrow \hspace{0.3cm} S = \frac{{\rm Pr(correct \hspace{0.15cm}decision)}} |
{{\rm Pr(wrong \hspace{0.15cm}decision) }} = \frac{(1-\varepsilon)^2 \cdot \varepsilon}{\varepsilon^2 \cdot (1-\varepsilon)}= \frac{(1-\varepsilon)}{\varepsilon}\hspace{0.05cm}.$$ | {{\rm Pr(wrong \hspace{0.15cm}decision) }} = \frac{(1-\varepsilon)^2 \cdot \varepsilon}{\varepsilon^2 \cdot (1-\varepsilon)}= \frac{(1-\varepsilon)}{\varepsilon}\hspace{0.05cm}.$$ | ||
| − | *With $\varepsilon = 0.269$ we get the following numerical values: | + | *With $\varepsilon = 0.269$ we get the following numerical values: |
:$$S = {0.731}/{0.269}\hspace{0.15cm}\underline {= 2.717}\hspace{0.3cm}\Rightarrow | :$$S = {0.731}/{0.269}\hspace{0.15cm}\underline {= 2.717}\hspace{0.3cm}\Rightarrow | ||
\hspace{0.3cm}{\rm ln}\hspace{0.15cm}(S)\hspace{0.15cm} \underline {= 1}\hspace{0.05cm}.$$ | \hspace{0.3cm}{\rm ln}\hspace{0.15cm}(S)\hspace{0.15cm} \underline {= 1}\hspace{0.05cm}.$$ | ||
| + | [[File:P_ID2988__KC_A_4_3e_v1.png|rightr|frame| Iterative decoding of $(+1, -1, +1)$]] | ||
| + | '''(4)''' The sign of the channel log likelihood ratios $L_{\rm K}(i)$ is | ||
| + | *positive if $y_i = 0$, and | ||
| + | |||
| + | *negative for $y_i = 1$. | ||
| − | + | ||
| − | + | The absolute value $|L_{\rm K}(i)|$ indicates the reliability of $y_i$. | |
| − | + | *In the BSC model, $|L_{\rm K}(i)| = \ln {(1 \, – \varepsilon)/\varepsilon} = 1$ for all $i$. Thus: | |
:$$\underline {L_{\rm K}}(1)\hspace{0.15cm} \underline {= +1}\hspace{0.05cm},\hspace{0.5cm} | :$$\underline {L_{\rm K}}(1)\hspace{0.15cm} \underline {= +1}\hspace{0.05cm},\hspace{0.5cm} | ||
\underline {L_{\rm K}}(2)\hspace{0.15cm} \underline {= -1}\hspace{0.05cm},\hspace{0.5cm} | \underline {L_{\rm K}}(2)\hspace{0.15cm} \underline {= -1}\hspace{0.05cm},\hspace{0.5cm} | ||
| Line 138: | Line 145: | ||
| − | '''(5)''' The adjacent table illustrates the iterative | + | '''(5)''' The adjacent table illustrates the iterative bit-wise decoding starting from $\underline{y}_2 = (0, \, 1, \, 0)$. |
| − | + | ||
These results can be interpreted as follows: | These results can be interpreted as follows: | ||
| − | * The preassignment (iteration $I = 0$ | + | * The preassignment $($iteration $I = 0)$ happens according to $\underline{L}_{\rm APP} = \underline{L}_{\rm K}$. A hard decision ⇒ "$\sign \ {\underline{L}_{\rm APP}(i)}$" would lead to the decoding result $(0, \, 1, \, 0)$. |
| − | * After the first iteration $(I = 1)$ all a posteriori | + | |
| + | *The reliability of this obviously incorrect result is given as $|{\it \Sigma}_{\rm APP}| = 1$. This value agrees with $\ln (S)$ calculated in subtask '''(3)'''. | ||
| + | |||
| + | * After the first iteration $(I = 1)$ all a-posteriori log likelihood ratios are $L_{\rm APP}(i) = +1$. A hard decision here would yield the $($expected$)$ correct result $\underline{x}_{\rm APP} = (0, \, 0, \, 0)$. | ||
| + | |||
| + | *The probability that this outcome is correct is quantified by $|{\it \Sigma}_{\rm APP}| = 3$: | ||
:$${\rm ln}\hspace{0.25cm}\frac{{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)}{1-{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)} = 3 | :$${\rm ln}\hspace{0.25cm}\frac{{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)}{1-{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)} = 3 | ||
\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| Line 148: | Line 160: | ||
:$$\hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2) = {20}/{21} | :$$\hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2) = {20}/{21} | ||
{\approx 95.39\%}\hspace{0.05cm}.$$ | {\approx 95.39\%}\hspace{0.05cm}.$$ | ||
| − | * The second iteration confirms the decoding result of the first iteration. The reliability is even quantified here with | + | * The second iteration confirms the decoding result of the first iteration. The reliability is even quantified here with $9$. This value can be interpreted as follows: |
:$$\frac{{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)}{1-{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)} = {\rm e}^9 | :$$\frac{{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)}{1-{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)} = {\rm e}^9 | ||
\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2) = {{\rm e}^9}/{({\rm e}^9+1)} | {\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2) = {{\rm e}^9}/{({\rm e}^9+1)} | ||
\approx 99.99\% \hspace{0.05cm}.$$ | \approx 99.99\% \hspace{0.05cm}.$$ | ||
| − | *With each further iteration the reliability value and thus the probability ${\rm Pr}(\underline{x}_0 | \underline{y}_2)$ increases drastically ⇒ <u>All proposed solutions</u> are correct. | + | *With each further iteration the reliability value and thus the probability ${\rm Pr}(\underline{x}_0 | \underline{y}_2)$ increases drastically ⇒ <u>All proposed solutions</u> are correct. |
| + | |||
| + | [[File:P_ID2991__KC_A_4_3f_v1.png|right|frame|Iterative decoding of $(–1, –1, +1)$]] | ||
| + | '''(6)''' Correct are <u>the proposed solutions 2 and 3</u>: | ||
| + | *For the received vector $\underline{y}_6 = (1, \, 1, \, 0)$, the second table applies. | ||
| − | + | *The decoder now decides for the sequence $\underline{x}_1 = (1, \, 1, \, 1)$. | |
| − | + | ||
| − | + | *The case »$\underline{y}_6 = (1, \, 1, \, 0)$ received under the condition $\underline{x}_1 = (1, \, 1, \, 1)$ sent« would correspond exactly to the constellation »$\underline{y}_2 = (0, \, 1, \, 0)$ received and $\underline{x}_0 = (0, \, 0, \, 0)$ sent« considered in the last subtask. | |
| − | + | *But since $\underline{x}_0 = (0, \, 0, \, 0)$ was sent, there are now two bit errors with the following consequence: | |
| − | |||
| − | *But since $\underline{x}_0 = (0, \, 0, \, 0)$ was sent, there are now two bit errors with the following consequence: | ||
:* The iterative decoder decides incorrectly. | :* The iterative decoder decides incorrectly. | ||
| + | |||
:* With each further iteration the wrong decision is declared as more reliable. | :* With each further iteration the wrong decision is declared as more reliable. | ||
Latest revision as of 17:44, 30 November 2022
We consider in this exercise two codes:
- the "single parity–check code" ⇒ $\text{SPC (3, 2, 2)}$:
- $$\underline{x} = \big (\hspace{0.05cm}(0, 0, 0), \hspace{0.1cm} (0, 1, 1), \hspace{0.1cm} (1, 0, 1), \hspace{0.1cm} (1, 1, 0) \hspace{0.05cm} \big ) \hspace{0.05cm}, $$
- the repetition code ⇒ $\text{RC (3, 1, 3)}$:
- $$\underline{x} = \big (\hspace{0.05cm}(0, 0, 0), \hspace{0.1cm} (1, 1, 1) \hspace{0.05cm} \big ) \hspace{0.05cm}.$$
The channel is described at bit level by the $\text{BSC model}$. According to the graphic, the following applies:
- $${\rm Pr}(y_i \ne x_i) =\varepsilon = 0.269\hspace{0.05cm},$$
- $${\rm Pr}(y_i = x_i) =1-\varepsilon = 0.731\hspace{0.05cm}.$$
Here, $\varepsilon$ denotes the falsification probability of the BSC model.
Except for the last subtask, the following received value is always assumed:
- $$\underline{y} = (0, 1, 0) =\underline{y}_2 \hspace{0.05cm}. $$
The chosen indexing of all possible received vectors can be taken from the graphic.
- The most considered vector $\underline{y}_2$ is highlighted in red.
- Only for subtask (6) applies:
- $$\underline{y} = (1, 1, 0) =\underline{y}_6 \hspace{0.05cm}. $$
For decoding purposes, the exercise will examine:
- the "syndrome decoding", which follows the concept "hard decision maximum likelihood detection" $\rm (HD-ML)$ for the codes under consideration.
$($because soft values are not available at the BSC$)$;
- the bit-wise "Soft–in Soft–out Decoding" $\rm (SISO)$ according to this section.
Hints:
- This exercise refers to the chapter "Soft–in Soft–out Decoder".
- Reference is made in particular to the sections
- The code word selected by the decoder is denoted in the questions by $\underline{z}$.
Questions
Solution
- The received word $\underline{y}_2 = (0, 1, 0)$ is not a valid code word of the single parity–check code $\text{SPC (3, 2)}$. Thus, the first statement is false.
- In addition, since the $\text{SPC (3, 2)}$ has only the minimum distance $d_{\rm min} = 2$, no error can be corrected.
(2) Correct is the proposed solution 2:
- The possible code words at the $\text{RP (3, 1)}$ are $\underline{x}_0 = (0, 0, 0)$ and $\underline{x}_1 = (1, 1, 1)$.
- The minimum distance of this code is $d_{\rm min} = 3$, so $t = (d_{\rm min} \, - 1)/2 = 1$ error can be corrected.
- In addition to $\underline{y}_0 = (0, 0, 0)$, the received words $\underline{y}_1 = (0, 0, 1), \ \underline{y}_2 = (0, 1, 0)$, and $\underline{y}_4 = (1, 0, 0)$ are also assigned to the decoding result $\underline{x}_0 = (0, 0, 0)$.
(3) According to the BSC model, the conditional probability that $\underline{y}_2 = (0, 1, 0)$ is received, given that $\underline{x}_0 = (0, 0, 0)$ was sent:
- $${\rm Pr}(\underline{y} = \underline{y}_2 \hspace{0.1cm}| \hspace{0.1cm}\underline{x} = \underline{x}_0 ) = (1-\varepsilon)^2 \cdot \varepsilon\hspace{0.05cm}.$$
- The first term $(1 \, –\varepsilon)^2$ indicates the probability that the first and third bit were transmitted correctly. $\varepsilon$ describes the falsification probability for the second bit.
- Correspondingly, for the second possible code word $\underline{x}_1 = (1, 1, 1)$:
- $${\rm Pr}(\underline{y} = \underline{y}_2 \hspace{0.1cm}| \hspace{0.1cm}\underline{x} = \underline{x}_1 ) = \varepsilon^2 \cdot (1-\varepsilon) \hspace{0.05cm}.$$
- According to Bayes' theorem, the inference probabilities are then:
- $${\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y} = \underline{y}_2 ) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Pr}(\underline{y} = \underline{y}_2 \hspace{0.1cm}| \hspace{0.1cm}\underline{x} = \underline{x}_0 ) \cdot \frac{{\rm Pr}(\underline{x} = \underline{x}_0)} {{\rm Pr}(\underline{y} = \underline{y}_2)} \hspace{0.05cm},$$
- $${\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_1 \hspace{0.1cm}| \hspace{0.1cm}\underline{y} = \underline{y}_2 ) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Pr}(\underline{y} = \underline{y}_2 \hspace{0.1cm}| \hspace{0.1cm}\underline{x} = \underline{x}_1 ) \cdot \frac{{\rm Pr}(\underline{x} = \underline{x}_1)} {{\rm Pr}(\underline{y} = \underline{y}_2)} $$
- $$\Rightarrow \hspace{0.3cm} S = \frac{{\rm Pr(correct \hspace{0.15cm}decision)}} {{\rm Pr(wrong \hspace{0.15cm}decision) }} = \frac{(1-\varepsilon)^2 \cdot \varepsilon}{\varepsilon^2 \cdot (1-\varepsilon)}= \frac{(1-\varepsilon)}{\varepsilon}\hspace{0.05cm}.$$
- With $\varepsilon = 0.269$ we get the following numerical values:
- $$S = {0.731}/{0.269}\hspace{0.15cm}\underline {= 2.717}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm ln}\hspace{0.15cm}(S)\hspace{0.15cm} \underline {= 1}\hspace{0.05cm}.$$
(4) The sign of the channel log likelihood ratios $L_{\rm K}(i)$ is
- positive if $y_i = 0$, and
- negative for $y_i = 1$.
The absolute value $|L_{\rm K}(i)|$ indicates the reliability of $y_i$.
- In the BSC model, $|L_{\rm K}(i)| = \ln {(1 \, – \varepsilon)/\varepsilon} = 1$ for all $i$. Thus:
- $$\underline {L_{\rm K}}(1)\hspace{0.15cm} \underline {= +1}\hspace{0.05cm},\hspace{0.5cm} \underline {L_{\rm K}}(2)\hspace{0.15cm} \underline {= -1}\hspace{0.05cm},\hspace{0.5cm} \underline {L_{\rm K}}(3)\hspace{0.15cm} \underline {= +1}\hspace{0.05cm}.$$
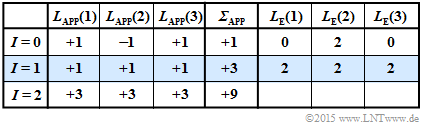
(5) The adjacent table illustrates the iterative bit-wise decoding starting from $\underline{y}_2 = (0, \, 1, \, 0)$.
These results can be interpreted as follows:
- The preassignment $($iteration $I = 0)$ happens according to $\underline{L}_{\rm APP} = \underline{L}_{\rm K}$. A hard decision ⇒ "$\sign \ {\underline{L}_{\rm APP}(i)}$" would lead to the decoding result $(0, \, 1, \, 0)$.
- The reliability of this obviously incorrect result is given as $|{\it \Sigma}_{\rm APP}| = 1$. This value agrees with $\ln (S)$ calculated in subtask (3).
- After the first iteration $(I = 1)$ all a-posteriori log likelihood ratios are $L_{\rm APP}(i) = +1$. A hard decision here would yield the $($expected$)$ correct result $\underline{x}_{\rm APP} = (0, \, 0, \, 0)$.
- The probability that this outcome is correct is quantified by $|{\it \Sigma}_{\rm APP}| = 3$:
- $${\rm ln}\hspace{0.25cm}\frac{{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)}{1-{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)} = 3 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \frac{{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)}{1-{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)} = {\rm e}^3 \approx 20$$
- $$\hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2) = {20}/{21} {\approx 95.39\%}\hspace{0.05cm}.$$
- The second iteration confirms the decoding result of the first iteration. The reliability is even quantified here with $9$. This value can be interpreted as follows:
- $$\frac{{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)}{1-{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)} = {\rm e}^9 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2) = {{\rm e}^9}/{({\rm e}^9+1)} \approx 99.99\% \hspace{0.05cm}.$$
- With each further iteration the reliability value and thus the probability ${\rm Pr}(\underline{x}_0 | \underline{y}_2)$ increases drastically ⇒ All proposed solutions are correct.
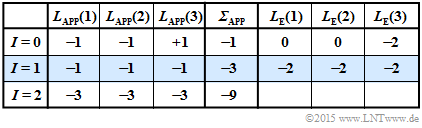
(6) Correct are the proposed solutions 2 and 3:
- For the received vector $\underline{y}_6 = (1, \, 1, \, 0)$, the second table applies.
- The decoder now decides for the sequence $\underline{x}_1 = (1, \, 1, \, 1)$.
- The case »$\underline{y}_6 = (1, \, 1, \, 0)$ received under the condition $\underline{x}_1 = (1, \, 1, \, 1)$ sent« would correspond exactly to the constellation »$\underline{y}_2 = (0, \, 1, \, 0)$ received and $\underline{x}_0 = (0, \, 0, \, 0)$ sent« considered in the last subtask.
- But since $\underline{x}_0 = (0, \, 0, \, 0)$ was sent, there are now two bit errors with the following consequence:
- The iterative decoder decides incorrectly.
- With each further iteration the wrong decision is declared as more reliable.