Difference between revisions of "Aufgaben:Exercise 4.1: Log Likelihood Ratio"
| (5 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
{{quiz-Header|Buchseite=Channel_Coding/Soft-in_Soft-Out_Decoder}} | {{quiz-Header|Buchseite=Channel_Coding/Soft-in_Soft-Out_Decoder}} | ||
| − | [[File: | + | [[File:EN_KC_A_4_1.png|right|frame|Considered channel models]] |
To interpret the "log likelihood ratio" $\rm (LLR)$ we start from the "binary symmetric channel" $\rm (BSC)$ as in the [[Channel_Coding/Soft-in_Soft-Out_Decoder#Reliability_information_-_Log_Likelihood_Ratio|"theory section"]] . | To interpret the "log likelihood ratio" $\rm (LLR)$ we start from the "binary symmetric channel" $\rm (BSC)$ as in the [[Channel_Coding/Soft-in_Soft-Out_Decoder#Reliability_information_-_Log_Likelihood_Ratio|"theory section"]] . | ||
| Line 19: | Line 19: | ||
:$$L_{\rm A}(x)={\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = 0)}{{\rm Pr}(x = 1)}\hspace{0.05cm},$$ | :$$L_{\rm A}(x)={\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = 0)}{{\rm Pr}(x = 1)}\hspace{0.05cm},$$ | ||
| − | where the subscript $\rm A$ indicates the "a-priori log likelihood ratio" or the "a-priori L–value". | + | where the subscript "$\rm A$" indicates the "a-priori log likelihood ratio" or the "a-priori L–value". |
For example, for ${\rm Pr}(x = 0) = 0.2 \ \Rightarrow \ {\rm Pr}(x = 1) = 0.8$ ⇒ $L_{\rm A}(x) = \, -1.382$. | For example, for ${\rm Pr}(x = 0) = 0.2 \ \Rightarrow \ {\rm Pr}(x = 1) = 0.8$ ⇒ $L_{\rm A}(x) = \, -1.382$. | ||
| − | From the BSC& | + | From the BSC model, it is possible to determine the L–value of the conditional probabilities ${\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x)$ in forward direction $($German: "Vorwärtsrichtung" ⇒ subscript "V"$)$, which is denoted by $L_{\rm V}(y)$ in the present exercise: |
:$$L_{\rm V}(y) = L(y\hspace{0.05cm}|\hspace{0.05cm}x) = | :$$L_{\rm V}(y) = L(y\hspace{0.05cm}|\hspace{0.05cm}x) = | ||
{\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x = 0)}{{\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x = 1)} = | {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x = 0)}{{\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x = 1)} = | ||
| Line 31: | Line 31: | ||
\\ {\rm f\ddot{u}r} \hspace{0.15cm} y = 1. \\ \end{array}$$ | \\ {\rm f\ddot{u}r} \hspace{0.15cm} y = 1. \\ \end{array}$$ | ||
| − | For example, for $\varepsilon = 0.1$: | + | For example, for $\varepsilon = 0.1$: |
:$$L_{\rm V}(y = 0) = +2.197\hspace{0.05cm}, \hspace{0.3cm}L_{\rm V}(y = 1) = -2.197\hspace{0.05cm}.$$ | :$$L_{\rm V}(y = 0) = +2.197\hspace{0.05cm}, \hspace{0.3cm}L_{\rm V}(y = 1) = -2.197\hspace{0.05cm}.$$ | ||
| − | Of particular importance to coding theory are the inference probabilities ${\rm Pr}(x\hspace{0.05cm}|\hspace{0.05cm}y)$, which are related to the | + | Of particular importance to coding theory are the inference probabilities ${\rm Pr}(x\hspace{0.05cm}|\hspace{0.05cm}y)$, which are related to the backward probabilities ${\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x)$ and the input probabilities ${\rm Pr}(x = 0)$ and ${\rm Pr}(x = 1)$ via Bayes' theorem. |
| − | The corresponding | + | The corresponding L–value in backward direction $($German: "Rückwärtsrichtung" ⇒ subscript "R"$)$ is denoted in this exercise by $L_{\rm R}(y)$: |
:$$L_{\rm R}(y) = L(x\hspace{0.05cm}|\hspace{0.05cm}y) = | :$$L_{\rm R}(y) = L(x\hspace{0.05cm}|\hspace{0.05cm}y) = | ||
{\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = 0)\hspace{0.05cm}|\hspace{0.05cm}y)}{{\rm Pr}(x = 1)\hspace{0.05cm}|\hspace{0.05cm}y)} \hspace{0.05cm} .$$ | {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = 0)\hspace{0.05cm}|\hspace{0.05cm}y)}{{\rm Pr}(x = 1)\hspace{0.05cm}|\hspace{0.05cm}y)} \hspace{0.05cm} .$$ | ||
| Line 44: | Line 44: | ||
| + | <u>Hints:</u> | ||
| + | * The exercise belongs to the chapter [[Channel_Coding/Soft-in_Soft-Out_Decoder| "Soft–in Soft–out Decoder"]]. | ||
| + | * Reference is made in particular to the section [[Channel_Coding/Soft-in_Soft-Out_Decoder#Reliability_information_-_Log_Likelihood_Ratio| "Reliability Information – Log Likelihood Ratio"]]. | ||
| − | + | *In the last subtasks you have to clarify whether the found relations between $L_{\rm A}, \ L_{\rm V}$ and $L_{\rm R}$ can also be transferred to the "2-on-$M$ channel". | |
| − | + | ||
| − | + | *For this purpose, we choose a bipolar approach for the input symbols: "$0$" → "$+1$" and "$1$" → "$–1$". | |
| − | |||
| − | |||
| − | *In the last subtasks | ||
| − | *For this purpose, we choose a bipolar approach for the input symbols: "$0$" → "$+1$" and "$1$" → "$–1$". | ||
| Line 70: | Line 69: | ||
- ${\rm Pr}(x = 0 | y = 0) = {\rm Pr}(y = 0 | x = 0) \cdot {\rm Pr}(y = 0) / {\rm Pr}(x = 0)$. | - ${\rm Pr}(x = 0 | y = 0) = {\rm Pr}(y = 0 | x = 0) \cdot {\rm Pr}(y = 0) / {\rm Pr}(x = 0)$. | ||
| − | {Under what conditions does the inference | + | {Under what conditions does the inference log likelihood ratio hold for all possible output values $y ∈ \{0, \, 1\}$: $L(x\hspace{0.05cm}|\hspace{0.05cm}y) = L(y\hspace{0.05cm}|\hspace{0.05cm}x)$ resp. $L_{\rm R}(y) = L_{\rm V}(y)$? |
|type="()"} | |type="()"} | ||
- For any input distribution ${\rm Pr}(x = 0), \ {\rm Pr}(x = 1)$. | - For any input distribution ${\rm Pr}(x = 0), \ {\rm Pr}(x = 1)$. | ||
+ For the uniform distribution only: $\hspace{0.2cm} {\rm Pr}(x = 0) = {\rm Pr}(x = 1) = 1/2$. | + For the uniform distribution only: $\hspace{0.2cm} {\rm Pr}(x = 0) = {\rm Pr}(x = 1) = 1/2$. | ||
| − | {Let the initial symbol be $y = 1$. What inference LLR is obtained with the | + | {Let the initial symbol be $y = 1$. What inference LLR is obtained with the falsification probability $\varepsilon = 0.1$ for equally probable symbols? |
|type="{}"} | |type="{}"} | ||
$L_{\rm R}(y = 1) = L(x | y = 1) \ = \ ${ -2.26291--2.13109 } | $L_{\rm R}(y = 1) = L(x | y = 1) \ = \ ${ -2.26291--2.13109 } | ||
| − | {Let the initial symbol now be $y = 0$. What inference | + | {Let the initial symbol now be $y = 0$. What inference log likelihood ratio is obtained for ${\rm Pr}(x = 0) = 0.2$ and $\varepsilon = 0.1$? |
|type="{}"} | |type="{}"} | ||
$L_{\rm R}(y = 0) = L(x | y = 0) \ = \ ${ 0.815 3% } | $L_{\rm R}(y = 0) = L(x | y = 0) \ = \ ${ 0.815 3% } | ||
| − | {Can the result derived in '''(3) | + | {Can the result derived in subtask '''(3)''' ⇒ $L_{\rm R} = L_{\rm V} + L_{\rm A}$ also be applied to the "2-on-''M''" channel? |
|type="()"} | |type="()"} | ||
+ Yes. | + Yes. | ||
- No. | - No. | ||
| − | {Can the context be applied to the AWGN | + | {Can the context be applied to the AWGN channel as well? |
|type="()"} | |type="()"} | ||
+ Yes. | + Yes. | ||
| Line 96: | Line 95: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' For the conditional probabilities, according to the [[Theory_of_Stochastic_Signals/Statistical_Dependence_and_Independence#Conditional_Probability| "Bayes' theorem"]] with intersection $A ∩ B$: | + | '''(1)''' For the conditional probabilities, according to the [[Theory_of_Stochastic_Signals/Statistical_Dependence_and_Independence#Conditional_Probability| "Bayes' theorem"]] with intersection $A ∩ B$: |
:$${\rm Pr}(B \hspace{0.05cm}|\hspace{0.05cm} A) = \frac{{\rm Pr}(A \cap B)}{{\rm Pr}(A)}\hspace{0.05cm}, | :$${\rm Pr}(B \hspace{0.05cm}|\hspace{0.05cm} A) = \frac{{\rm Pr}(A \cap B)}{{\rm Pr}(A)}\hspace{0.05cm}, | ||
\hspace{0.3cm} {\rm Pr}(A \hspace{0.05cm}|\hspace{0.05cm} B) = \frac{{\rm Pr}(A \cap B)}{{\rm Pr}(B)}\hspace{0.3cm} | \hspace{0.3cm} {\rm Pr}(A \hspace{0.05cm}|\hspace{0.05cm} B) = \frac{{\rm Pr}(A \cap B)}{{\rm Pr}(B)}\hspace{0.3cm} | ||
| Line 102: | Line 101: | ||
{\rm Pr}(B \hspace{0.05cm}|\hspace{0.05cm} A) \cdot \frac{{\rm Pr}(A)}{{\rm Pr}(B)}\hspace{0.05cm}.$$ | {\rm Pr}(B \hspace{0.05cm}|\hspace{0.05cm} A) \cdot \frac{{\rm Pr}(A)}{{\rm Pr}(B)}\hspace{0.05cm}.$$ | ||
| − | Correct is the <u>proposition 3</u>. | + | *Correct is the <u>proposition 3</u>. |
| + | *In the special case ${\rm Pr}(B) = {\rm Pr}(A)$ ⇒ also the suggestion 1 would be correct. | ||
| − | '''(2)''' With $A$ ⇒ "$x = 0$" and $B$ ⇒ "$y = 0$" we immediately get the equation according to <u>proposition 1</u>: | + | |
| + | |||
| + | '''(2)''' With $A$ ⇒ "$x = 0$" and $B$ ⇒ "$y = 0$" we immediately get the equation according to <u>proposition 1</u>: | ||
:$${\rm Pr}(x = 0\hspace{0.05cm}|\hspace{0.05cm} y = 0) = | :$${\rm Pr}(x = 0\hspace{0.05cm}|\hspace{0.05cm} y = 0) = | ||
{\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x = 0) \cdot \frac{{\rm Pr}(x = 0)}{{\rm Pr}(y = 0)}\hspace{0.05cm}.$$ | {\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x = 0) \cdot \frac{{\rm Pr}(x = 0)}{{\rm Pr}(y = 0)}\hspace{0.05cm}.$$ | ||
| − | '''(3)''' We compute the | + | '''(3)''' We compute the L–values of the inference probabilities. Assuming $y = 0$ holds: |
:$$L_{\rm R}(y= 0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} L(x\hspace{0.05cm}|\hspace{0.05cm}y= 0)= | :$$L_{\rm R}(y= 0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} L(x\hspace{0.05cm}|\hspace{0.05cm}y= 0)= | ||
{\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = 0\hspace{0.05cm}|\hspace{0.05cm}y=0)}{{\rm Pr}(x = 1\hspace{0.05cm}|\hspace{0.05cm}y=0)} = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm}x=0) \cdot {\rm Pr}(x = 0) / {\rm Pr}(y = 0)}{{\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm}x = 1)\cdot {\rm Pr}(x = 1) / {\rm Pr}(y = 0)} $$ | {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = 0\hspace{0.05cm}|\hspace{0.05cm}y=0)}{{\rm Pr}(x = 1\hspace{0.05cm}|\hspace{0.05cm}y=0)} = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm}x=0) \cdot {\rm Pr}(x = 0) / {\rm Pr}(y = 0)}{{\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm}x = 1)\cdot {\rm Pr}(x = 1) / {\rm Pr}(y = 0)} $$ | ||
| Line 117: | Line 119: | ||
:$$\Rightarrow \hspace{0.3cm} L_{\rm R}(y= 0) = L(x\hspace{0.05cm}|\hspace{0.05cm}y= 0) = L_{\rm V}(y= 0) + L_{\rm A}(x)\hspace{0.05cm}.$$ | :$$\Rightarrow \hspace{0.3cm} L_{\rm R}(y= 0) = L(x\hspace{0.05cm}|\hspace{0.05cm}y= 0) = L_{\rm V}(y= 0) + L_{\rm A}(x)\hspace{0.05cm}.$$ | ||
| − | Similarly, assuming $y = 1$, the result is: | + | *Similarly, assuming $y = 1$, the result is: |
:$$L_{\rm R}(y= 1) = L(x\hspace{0.05cm}|\hspace{0.05cm}y= 1) = L_{\rm V}(y= 1) + L_{\rm A}(x)\hspace{0.05cm}.$$ | :$$L_{\rm R}(y= 1) = L(x\hspace{0.05cm}|\hspace{0.05cm}y= 1) = L_{\rm V}(y= 1) + L_{\rm A}(x)\hspace{0.05cm}.$$ | ||
| − | The two results can be summarized using $y ∈ \{0, \, 1\}$ and | + | *The two results can be summarized using $y ∈ \{0, \, 1\}$ and |
| − | * the input | + | |
| − | :$$L_{\rm A}(x) = | + | * the input log likelihood ratio, |
| − | {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x=0) }{\rm Pr}(x = 1)}\hspace{0.05cm},$$ | + | :$$L_{\rm A}(x) = {\rm ln} \hspace{0.15cm} \frac{ {\rm Pr}(x=0) }{ {\rm Pr}(x = 1)}\hspace{0.05cm},$$ |
| − | * as well as the forward | + | |
| + | * as well as the forward log likelihood ratio, | ||
:$$L_{\rm V}(y) = L(y\hspace{0.05cm}|\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y \hspace{0.05cm}|\hspace{0.05cm}x=0) }{{\rm Pr}(y \hspace{0.05cm}|\hspace{0.05cm}x = 1)} | :$$L_{\rm V}(y) = L(y\hspace{0.05cm}|\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y \hspace{0.05cm}|\hspace{0.05cm}x=0) }{{\rm Pr}(y \hspace{0.05cm}|\hspace{0.05cm}x = 1)} | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| Line 131: | Line 134: | ||
:$$L_{\rm R}(y) = L(x\hspace{0.05cm}|\hspace{0.05cm}y) = L_{\rm V}(y) + L_{\rm A}(x)\hspace{0.05cm}.$$ | :$$L_{\rm R}(y) = L(x\hspace{0.05cm}|\hspace{0.05cm}y) = L_{\rm V}(y) + L_{\rm A}(x)\hspace{0.05cm}.$$ | ||
| − | The identity $L_{\rm R}(y) ≡ L_{\rm V}(y)$ requires $L_{\rm A}(x) = 0$ ⇒ equally probable symbols ⇒ <u>proposition 2</u>. | + | *The identity $L_{\rm R}(y) ≡ L_{\rm V}(y)$ requires $L_{\rm A}(x) = 0$ ⇒ equally probable symbols ⇒ <u>proposition 2</u>. |
| − | |||
| − | * | + | '''(4)''' From the exercise description, you can see that with falsification probability $\varepsilon = 0.1$, the initial value $y = 1$ leads to forward log likelihood ratio $L_{\rm V}(y = 1) = \, –2.197$. |
| + | |||
| + | *Because of ${\rm Pr}(x = 0) = 1/2 \ \Rightarrow \ L_{\rm A}(x) = 0$: | ||
:$$L_{\rm R}(y = 1) = L_{\rm V}(y = 1) \hspace{0.15cm}\underline{= -2.197}\hspace{0.05cm}.$$ | :$$L_{\rm R}(y = 1) = L_{\rm V}(y = 1) \hspace{0.15cm}\underline{= -2.197}\hspace{0.05cm}.$$ | ||
| − | '''(5)''' With the same | + | |
| − | *With ${\rm Pr}(x = 0) = 0.2 \ \Rightarrow \ L_{\rm A}(x) = \, -1.382$ we thus obtain: | + | '''(5)''' With the same falsification probability $\varepsilon = 0.1$ ⇒ $L_{\rm V}(y = 0)$ differs from $L_{\rm V}(y = 1)$ only by the sign. |
| + | *With ${\rm Pr}(x = 0) = 0.2 \ \Rightarrow \ L_{\rm A}(x) = \, -1.382$ we thus obtain: | ||
:$$L_{\rm R}(y = 0) = (+)2.197 - 1.382 \hspace{0.15cm}\underline{=+0.815}\hspace{0.05cm}.$$ | :$$L_{\rm R}(y = 0) = (+)2.197 - 1.382 \hspace{0.15cm}\underline{=+0.815}\hspace{0.05cm}.$$ | ||
| − | '''(6)''' | + | '''(6)''' The relation $L_{\rm R} = L_{\rm V} + L_{\rm A}$ also holds for the "2-on-$M$ channel", regardless of the set size $M$ of the output alphabet ⇒ <u>Answer Yes</u>. |
| − | '''(7)''' The AWGN channel is described by the outlined "2–on–$M$–channel" with $M → ∞$ also ⇒ <u>Answer Yes</u>. | + | '''(7)''' The AWGN channel is described by the outlined "2–on–$M$–channel" with $M → ∞$ also ⇒ <u>Answer Yes</u>. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
[[Category:Channel Coding: Exercises|^4.1 Soft–in Soft–out Decoder^]] | [[Category:Channel Coding: Exercises|^4.1 Soft–in Soft–out Decoder^]] | ||
Latest revision as of 16:27, 23 January 2023
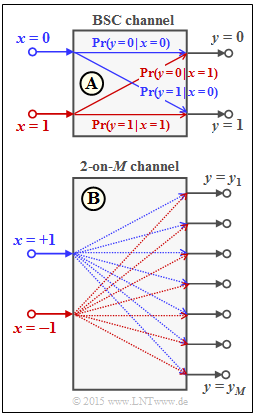
To interpret the "log likelihood ratio" $\rm (LLR)$ we start from the "binary symmetric channel" $\rm (BSC)$ as in the "theory section" .
For the binary random variables at the channel input and output holds:
- $$x \in \{0\hspace{0.05cm}, 1\} \hspace{0.05cm},\hspace{0.25cm}y \in \{0\hspace{0.05cm}, 1\} \hspace{0.05cm}. $$
This model is shown in the upper graph. The following applies to the conditional probabilities in the forward direction:
- $${\rm Pr}(y = 1\hspace{0.05cm}|\hspace{0.05cm} x = 0) = {\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x = 1) = \varepsilon \hspace{0.05cm},$$
- $${\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x = 0) = {\rm Pr}(y = 1\hspace{0.05cm}|\hspace{0.05cm} x = 1) = 1-\varepsilon \hspace{0.05cm}.$$
The falsification probability $\varepsilon$ is the crucial parameter of the BSC model.
Regarding the probability distribution at the input instead of considering the probabilities ${\rm Pr}(x = 0)$ and ${\rm Pr}(x = 1)$ it is convenient to consider the log likelihood ratio.
For the unipolar approach used here, the following applies by definition:
- $$L_{\rm A}(x)={\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = 0)}{{\rm Pr}(x = 1)}\hspace{0.05cm},$$
where the subscript "$\rm A$" indicates the "a-priori log likelihood ratio" or the "a-priori L–value".
For example, for ${\rm Pr}(x = 0) = 0.2 \ \Rightarrow \ {\rm Pr}(x = 1) = 0.8$ ⇒ $L_{\rm A}(x) = \, -1.382$.
From the BSC model, it is possible to determine the L–value of the conditional probabilities ${\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x)$ in forward direction $($German: "Vorwärtsrichtung" ⇒ subscript "V"$)$, which is denoted by $L_{\rm V}(y)$ in the present exercise:
- $$L_{\rm V}(y) = L(y\hspace{0.05cm}|\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x = 0)}{{\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x = 1)} = \left\{ \begin{array}{c} {\rm ln} \hspace{0.15cm} [(1 - \varepsilon)/\varepsilon]\\ {\rm ln} \hspace{0.15cm} [\varepsilon/(1 - \varepsilon)] \end{array} \right.\hspace{0.15cm} \begin{array}{*{1}c} {\rm f\ddot{u}r} \hspace{0.15cm} y = 0, \\ {\rm f\ddot{u}r} \hspace{0.15cm} y = 1. \\ \end{array}$$
For example, for $\varepsilon = 0.1$:
- $$L_{\rm V}(y = 0) = +2.197\hspace{0.05cm}, \hspace{0.3cm}L_{\rm V}(y = 1) = -2.197\hspace{0.05cm}.$$
Of particular importance to coding theory are the inference probabilities ${\rm Pr}(x\hspace{0.05cm}|\hspace{0.05cm}y)$, which are related to the backward probabilities ${\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x)$ and the input probabilities ${\rm Pr}(x = 0)$ and ${\rm Pr}(x = 1)$ via Bayes' theorem.
The corresponding L–value in backward direction $($German: "Rückwärtsrichtung" ⇒ subscript "R"$)$ is denoted in this exercise by $L_{\rm R}(y)$:
- $$L_{\rm R}(y) = L(x\hspace{0.05cm}|\hspace{0.05cm}y) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = 0)\hspace{0.05cm}|\hspace{0.05cm}y)}{{\rm Pr}(x = 1)\hspace{0.05cm}|\hspace{0.05cm}y)} \hspace{0.05cm} .$$
Hints:
- The exercise belongs to the chapter "Soft–in Soft–out Decoder".
- Reference is made in particular to the section "Reliability Information – Log Likelihood Ratio".
- In the last subtasks you have to clarify whether the found relations between $L_{\rm A}, \ L_{\rm V}$ and $L_{\rm R}$ can also be transferred to the "2-on-$M$ channel".
- For this purpose, we choose a bipolar approach for the input symbols: "$0$" → "$+1$" and "$1$" → "$–1$".
Questions
Solution
- $${\rm Pr}(B \hspace{0.05cm}|\hspace{0.05cm} A) = \frac{{\rm Pr}(A \cap B)}{{\rm Pr}(A)}\hspace{0.05cm}, \hspace{0.3cm} {\rm Pr}(A \hspace{0.05cm}|\hspace{0.05cm} B) = \frac{{\rm Pr}(A \cap B)}{{\rm Pr}(B)}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm Pr}(A \hspace{0.05cm}|\hspace{0.05cm} B) = {\rm Pr}(B \hspace{0.05cm}|\hspace{0.05cm} A) \cdot \frac{{\rm Pr}(A)}{{\rm Pr}(B)}\hspace{0.05cm}.$$
- Correct is the proposition 3.
- In the special case ${\rm Pr}(B) = {\rm Pr}(A)$ ⇒ also the suggestion 1 would be correct.
(2) With $A$ ⇒ "$x = 0$" and $B$ ⇒ "$y = 0$" we immediately get the equation according to proposition 1:
- $${\rm Pr}(x = 0\hspace{0.05cm}|\hspace{0.05cm} y = 0) = {\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x = 0) \cdot \frac{{\rm Pr}(x = 0)}{{\rm Pr}(y = 0)}\hspace{0.05cm}.$$
(3) We compute the L–values of the inference probabilities. Assuming $y = 0$ holds:
- $$L_{\rm R}(y= 0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} L(x\hspace{0.05cm}|\hspace{0.05cm}y= 0)= {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = 0\hspace{0.05cm}|\hspace{0.05cm}y=0)}{{\rm Pr}(x = 1\hspace{0.05cm}|\hspace{0.05cm}y=0)} = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm}x=0) \cdot {\rm Pr}(x = 0) / {\rm Pr}(y = 0)}{{\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm}x = 1)\cdot {\rm Pr}(x = 1) / {\rm Pr}(y = 0)} $$
- $$\Rightarrow \hspace{0.3cm} L_{\rm R}(y= 0)= {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm}x=0) }{{\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm}x = 1)} + {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x=0) }{{\rm Pr}(x = 1)}$$
- $$\Rightarrow \hspace{0.3cm} L_{\rm R}(y= 0) = L(x\hspace{0.05cm}|\hspace{0.05cm}y= 0) = L_{\rm V}(y= 0) + L_{\rm A}(x)\hspace{0.05cm}.$$
- Similarly, assuming $y = 1$, the result is:
- $$L_{\rm R}(y= 1) = L(x\hspace{0.05cm}|\hspace{0.05cm}y= 1) = L_{\rm V}(y= 1) + L_{\rm A}(x)\hspace{0.05cm}.$$
- The two results can be summarized using $y ∈ \{0, \, 1\}$ and
- the input log likelihood ratio,
- $$L_{\rm A}(x) = {\rm ln} \hspace{0.15cm} \frac{ {\rm Pr}(x=0) }{ {\rm Pr}(x = 1)}\hspace{0.05cm},$$
- as well as the forward log likelihood ratio,
- $$L_{\rm V}(y) = L(y\hspace{0.05cm}|\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y \hspace{0.05cm}|\hspace{0.05cm}x=0) }{{\rm Pr}(y \hspace{0.05cm}|\hspace{0.05cm}x = 1)} \hspace{0.05cm},$$
as follows:
- $$L_{\rm R}(y) = L(x\hspace{0.05cm}|\hspace{0.05cm}y) = L_{\rm V}(y) + L_{\rm A}(x)\hspace{0.05cm}.$$
- The identity $L_{\rm R}(y) ≡ L_{\rm V}(y)$ requires $L_{\rm A}(x) = 0$ ⇒ equally probable symbols ⇒ proposition 2.
(4) From the exercise description, you can see that with falsification probability $\varepsilon = 0.1$, the initial value $y = 1$ leads to forward log likelihood ratio $L_{\rm V}(y = 1) = \, –2.197$.
- Because of ${\rm Pr}(x = 0) = 1/2 \ \Rightarrow \ L_{\rm A}(x) = 0$:
- $$L_{\rm R}(y = 1) = L_{\rm V}(y = 1) \hspace{0.15cm}\underline{= -2.197}\hspace{0.05cm}.$$
(5) With the same falsification probability $\varepsilon = 0.1$ ⇒ $L_{\rm V}(y = 0)$ differs from $L_{\rm V}(y = 1)$ only by the sign.
- With ${\rm Pr}(x = 0) = 0.2 \ \Rightarrow \ L_{\rm A}(x) = \, -1.382$ we thus obtain:
- $$L_{\rm R}(y = 0) = (+)2.197 - 1.382 \hspace{0.15cm}\underline{=+0.815}\hspace{0.05cm}.$$
(6) The relation $L_{\rm R} = L_{\rm V} + L_{\rm A}$ also holds for the "2-on-$M$ channel", regardless of the set size $M$ of the output alphabet ⇒ Answer Yes.
(7) The AWGN channel is described by the outlined "2–on–$M$–channel" with $M → ∞$ also ⇒ Answer Yes.