Difference between revisions of "Aufgaben:Exercise 1.2Z: Measurement of the Frequency Response"
| (47 intermediate revisions by 8 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Linear_and_Time_Invariant_Systems/System_Description_in_Frequency_Domain}} |
| − | |||
| − | |||
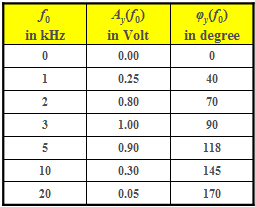
| − | + | [[File:EN_LZI_Z_1_2.png|right|Measured signal amplitudes <br>and phases for filter $\rm B$|frame]] | |
| − | $$|Y_{\rm A} (f)| = 1.6\hspace{0.05cm}{\rm V} \cdot {\rm \delta } (f | + | For the metrological determination of the filter frequency response a sinusoidal input signal with an amplitude of $2 \hspace{0.05cm} \text{V}$ and given frequency $f_0$ is applied. The output signal $y(t)$ or its spectrum $Y(f)$ are then determined according to magnitude and phase. |
| + | |||
| + | *The magnitude spectrum at the output of filter $\rm A$ with frequency $f_0 = 1 \ \text{kHz}$ is: | ||
| + | :$$|Y_{\rm A} (f)| = 1.6\hspace{0.05cm}{\rm V} \cdot {\rm \delta } (f | ||
\pm f_0) + 0.4\hspace{0.05cm}{\rm V} \cdot {\rm \delta } (f \pm 3 f_0) .$$ | \pm f_0) + 0.4\hspace{0.05cm}{\rm V} \cdot {\rm \delta } (f \pm 3 f_0) .$$ | ||
| − | + | *For another filter $\rm B$ the output signal is always a harmonic oscillation with the (single) frequency $f_0$. For the frequencies $f_0$ given in the table the amplitudes $A_y(f_0)$ and the phases $φ_y(f_0)$ are measured. Here, the following holds: | |
| − | $$Y_{\rm B} (f) = | + | :$$Y_{\rm B} (f) = {A_y}/{2} \cdot {\rm e}^{ {\rm j} \varphi_y} |
| − | \cdot {\rm \delta } (f + f_0) + | + | \cdot {\rm \delta } (f + f_0) + {A_y}/{2} \cdot {\rm e}^{ |
-{\rm j} \varphi_y} \cdot {\rm \delta } (f - f_0).$$ | -{\rm j} \varphi_y} \cdot {\rm \delta } (f - f_0).$$ | ||
| − | |||
| − | |||
| − | |||
| − | + | In the exercise, filter $\rm B$ should be given in the form:$$H_{\rm B}(f) = {\rm e}^{-a_{\rm B}(f)}\cdot {\rm e}^{-{\rm j} | |
| + | \hspace{0.05cm} \cdot \hspace{0.05cm} b_{\rm B}(f)}.$$ | ||
| + | |||
| + | Here, | ||
| + | *$a_{\rm B}(f_0)$ denotes the damping curve, and | ||
| + | *$b_{\rm B}(f_0)$ the phase response. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| − | '' | + | ''Please note:'' |
| + | *The task belongs to the chapter [[Linear_and_Time_Invariant_Systems/System_Description_in_Frequency_Domain | System Description in Frequency Domain]]. | ||
| + | |||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which of the statements are true regarding filter $\rm A$ ? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - The following holds: $|H(f)| = 0.8$. |
| − | + | + | + Filter $\rm A$ does not represent an LTI system. |
| − | + | + | + The specification of a frequency response is not possible. |
| − | { | + | {Which of the statements are true regarding filter $\rm B$ ? |
| − | |type=" | + | |type="()"} |
| − | - Filter B | + | - Filter $\rm B$ is a low-pass filter. |
| − | - Filter B | + | - Filter $\rm B$ is a high-pass filter. |
| − | + Filter B | + | + Filter $\rm B$ is a band-pass filter. |
| − | - Filter B | + | - Filter $\rm B$ is a band-stop filter. |
| − | { | + | {Determine the damping and the phase value for filter $\rm B$ and $f_0 = 3 \ \text{kHz}$. |
|type="{}"} | |type="{}"} | ||
| − | $a_{\rm B}(f_0 = \: \rm 3 \: kHz) =$ { 0.693 5% } Np | + | $a_{\rm B}(f_0 = \: \rm 3 \: kHz) \ = \ $ { 0.693 5% } $\text{Np}$ |
| − | $b_{\rm B}(f_0 = \: \rm 3 \: kHz) =$ { 0 } | + | $b_{\rm B}(f_0 = \: \rm 3 \: kHz) \ =\ $ { 0. } $\text{degree}$ |
| − | { | + | {What is the damping and phase value for $f_0 = 2 \ \text{kHz}$? |
|type="{}"} | |type="{}"} | ||
| − | $a_{\rm B}(f_0 = \: \rm 2 \: kHz) =$ { 0.916 5% } Np | + | $a_{\rm B}(f_0 = \: \rm 2 \: kHz) \ = \ $ { 0.916 5% } $\text{Np}$ |
| − | $b_{\rm B}(f_0 = \: \rm 2 \: kHz) =$ { 20 2% } | + | $b_{\rm B}(f_0 = \: \rm 2 \: kHz) \ =\ $ { 20 2% } $\text{degree}$ |
| Line 57: | Line 67: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' <u>Approaches 2 und 3</u> are correct: | |
| + | *For an LTI system, $Y(f) = X(f) · H(f)$ holds. | ||
| + | *Therefore, it is not possible for a component with $3 f_0$ to be present in the output signal if such a one is missing in the input signal. | ||
| + | *This means: There is no LTI system on hand and accordingly no frequency response can be specified. | ||
| + | |||
| + | |||
| + | '''(2)''' <u>Approach 3</u> is correct: | ||
| + | *Based on the given numerical values for $A_y(f_0)$ filter $\rm B$ can be assumed to be a <u>band-pass filter</u>. | ||
| − | |||
| − | + | '''(3)''' With $A_x = 2 \text{ V}$ and $\varphi_x = 90^\circ$ (sine function) the following is obtained for $f_0 = f_3 =3 \text{ kHz}$: | |
| − | $$H_{\rm B} (f_3) = \frac{A_y}{A_x} \cdot {\rm e}^{ -{\rm j} | + | :$$H_{\rm B} (f_3) = \frac{A_y}{A_x} \cdot {\rm e}^{ -{\rm j} |
(\varphi_x - \varphi_y)} = \frac{1\hspace{0.05cm}{\rm | (\varphi_x - \varphi_y)} = \frac{1\hspace{0.05cm}{\rm | ||
V}}{2\hspace{0.05cm}{\rm V}} \cdot {\rm e}^{ -{\rm j} (90^{\circ} - | V}}{2\hspace{0.05cm}{\rm V}} \cdot {\rm e}^{ -{\rm j} (90^{\circ} - | ||
90^{\circ})} = 0.5.$$ | 90^{\circ})} = 0.5.$$ | ||
| − | + | Thus, for $f_0 = f_3 = 3 \text{ kHz}$ the values | |
| + | *$a_{\rm B} (f_3)\rm \underline{\: ≈ \: 0.693 \: Np}$ and | ||
| + | *$b_{\rm B}(f_3) \rm \underline{\: = \: 0 \: (degree)}$ are determined. | ||
| − | + | '''(4)''' Analogously, the frequency response for $f_0 = f_2 =2 \text{ kHz}$ can be determined: | |
| − | $$H_{\rm B} ( f_2) = \frac{0.8\hspace{0.05cm}{\rm | + | :$$H_{\rm B} ( f_2) = \frac{0.8\hspace{0.05cm}{\rm |
V}}{2\hspace{0.05cm}{\rm V}} \cdot {\rm e}^{ -{\rm j} (90^{\circ} - | V}}{2\hspace{0.05cm}{\rm V}} \cdot {\rm e}^{ -{\rm j} (90^{\circ} - | ||
70^{\circ})} = 0.4\cdot {\rm e}^{ -{\rm j} 20^{\circ}}.$$ | 70^{\circ})} = 0.4\cdot {\rm e}^{ -{\rm j} 20^{\circ}}.$$ | ||
| − | + | Hence, for $f_0 = f_2 = 2 \ \text{ kHz}$: | |
| − | + | *$a_{\rm B}(f_2) \rm \underline{\: ≈ \: 0.916 \: Np}$, | |
| + | * $b_{\rm B}(f_2) \rm \underline{\: = \: 20°}$. | ||
| + | |||
| + | |||
| + | For $f_0 = -f_2 =-\hspace{-0.01cm}2 \text{ kHz}$ the same damping value applies. However, the phase has the opposite sign. So, $b_{\rm B}(–f_2) = \ –\hspace{-0.01cm}20^{\circ}.$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 84: | Line 106: | ||
| − | [[Category: | + | [[Category:Linear and Time-Invariant Systems: Exercises|^1.1 System Description in Frequency Domain^]] |
Latest revision as of 14:30, 7 October 2021
For the metrological determination of the filter frequency response a sinusoidal input signal with an amplitude of $2 \hspace{0.05cm} \text{V}$ and given frequency $f_0$ is applied. The output signal $y(t)$ or its spectrum $Y(f)$ are then determined according to magnitude and phase.
- The magnitude spectrum at the output of filter $\rm A$ with frequency $f_0 = 1 \ \text{kHz}$ is:
- $$|Y_{\rm A} (f)| = 1.6\hspace{0.05cm}{\rm V} \cdot {\rm \delta } (f \pm f_0) + 0.4\hspace{0.05cm}{\rm V} \cdot {\rm \delta } (f \pm 3 f_0) .$$
- For another filter $\rm B$ the output signal is always a harmonic oscillation with the (single) frequency $f_0$. For the frequencies $f_0$ given in the table the amplitudes $A_y(f_0)$ and the phases $φ_y(f_0)$ are measured. Here, the following holds:
- $$Y_{\rm B} (f) = {A_y}/{2} \cdot {\rm e}^{ {\rm j} \varphi_y} \cdot {\rm \delta } (f + f_0) + {A_y}/{2} \cdot {\rm e}^{ -{\rm j} \varphi_y} \cdot {\rm \delta } (f - f_0).$$
In the exercise, filter $\rm B$ should be given in the form:$$H_{\rm B}(f) = {\rm e}^{-a_{\rm B}(f)}\cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} b_{\rm B}(f)}.$$
Here,
- $a_{\rm B}(f_0)$ denotes the damping curve, and
- $b_{\rm B}(f_0)$ the phase response.
Please note:
- The task belongs to the chapter System Description in Frequency Domain.
Questions
Solution
- For an LTI system, $Y(f) = X(f) · H(f)$ holds.
- Therefore, it is not possible for a component with $3 f_0$ to be present in the output signal if such a one is missing in the input signal.
- This means: There is no LTI system on hand and accordingly no frequency response can be specified.
(2) Approach 3 is correct:
- Based on the given numerical values for $A_y(f_0)$ filter $\rm B$ can be assumed to be a band-pass filter.
(3) With $A_x = 2 \text{ V}$ and $\varphi_x = 90^\circ$ (sine function) the following is obtained for $f_0 = f_3 =3 \text{ kHz}$:
- $$H_{\rm B} (f_3) = \frac{A_y}{A_x} \cdot {\rm e}^{ -{\rm j} (\varphi_x - \varphi_y)} = \frac{1\hspace{0.05cm}{\rm V}}{2\hspace{0.05cm}{\rm V}} \cdot {\rm e}^{ -{\rm j} (90^{\circ} - 90^{\circ})} = 0.5.$$
Thus, for $f_0 = f_3 = 3 \text{ kHz}$ the values
- $a_{\rm B} (f_3)\rm \underline{\: ≈ \: 0.693 \: Np}$ and
- $b_{\rm B}(f_3) \rm \underline{\: = \: 0 \: (degree)}$ are determined.
(4) Analogously, the frequency response for $f_0 = f_2 =2 \text{ kHz}$ can be determined:
- $$H_{\rm B} ( f_2) = \frac{0.8\hspace{0.05cm}{\rm V}}{2\hspace{0.05cm}{\rm V}} \cdot {\rm e}^{ -{\rm j} (90^{\circ} - 70^{\circ})} = 0.4\cdot {\rm e}^{ -{\rm j} 20^{\circ}}.$$
Hence, for $f_0 = f_2 = 2 \ \text{ kHz}$:
- $a_{\rm B}(f_2) \rm \underline{\: ≈ \: 0.916 \: Np}$,
- $b_{\rm B}(f_2) \rm \underline{\: = \: 20°}$.
For $f_0 = -f_2 =-\hspace{-0.01cm}2 \text{ kHz}$ the same damping value applies. However, the phase has the opposite sign. So, $b_{\rm B}(–f_2) = \ –\hspace{-0.01cm}20^{\circ}.$