Difference between revisions of "Aufgaben:Exercise 1.3Z: Exponentially Decreasing Impulse Response"
From LNTwww
| (43 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Linear_and_Time_Invariant_Systems/System_Description_in_Time_Domain}} |
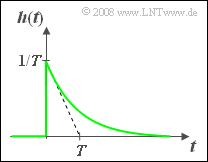
| − | [[File:P_ID819__LZI_Z_1_3.png |right| | + | [[File:P_ID819__LZI_Z_1_3.png |right|frame|Decreasing impulse response]] |
| − | + | The impulse response $h(t)$ of an LTI system, which | |
| − | $$h(t) = | + | *is identically zero for all times $t < 0$, |
| − | + | *changes abruptly at time $t > 0$, and | |
| − | $$|H(f = f_{\rm G})| = | + | *decreases for $t > 0$ according to an exponential function: |
| − | + | :$$h(t) = {1}/{T} \cdot {\rm e}^{-t/T},$$ was measured. | |
| − | + | Let the parameter be $T = 1 \hspace{0.15cm} \rm ms$. In the subtask '''(3)''' the 3dB cut-off frequency $f_{\rm G}$ is to be determined, which is (implicitly) defined as follows: | |
| + | :$$|H(f = f_{\rm G})| = {1}/{\sqrt{2}} \cdot|H(f = 0)| .$$ | ||
| − | === | + | |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Please note:'' | ||
| + | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/System_Description_in_Time_Domain|System Description in Time Domain]]. | ||
| + | *The following definite integral is given: | ||
| + | :$$\int_{ 0 }^{ \infty } \frac{1}{1+x^2} \hspace{0.1cm}{\rm d}x = {\pi}/{2} .$$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Compute the frequency response $H(f)$. What value is obtained for $f = 0$? |
|type="{}"} | |type="{}"} | ||
| − | $H(f = 0) =$ { 1 } | + | $H(f = 0) \ = \ $ { 1 3% } |
| − | { | + | {What is the value of the impulse response at time $t = 0$? |
|type="{}"} | |type="{}"} | ||
| − | $h(t = 0) =$ { 500 } 1/s | + | $h(t = 0) \ = \ $ { 500 3% } $\rm 1/s$ |
| − | { | + | {Compute the 3dB cut-off frequency $f_{\rm G}$. |
|type="{}"} | |type="{}"} | ||
| − | $f_{\rm G} =$ { 159 } Hz | + | $f_{\rm G} \ =\ $ { 159 3% } $\rm Hz$ |
| − | { | + | {Which of the following statements are true? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The considered system is causal. |
| − | - | + | - The considered system has high-pass filter characteristics. |
| − | - | + | - If a cosine signal of frequency $f_{\rm G}$ is applied to the system input, the output signal is also cosine-shaped. |
| Line 40: | Line 57: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' The frequency response $H(f)$ is the Fourier transform of $h(t)$: |
| − | $$H(f) = \int_{-\infty}^{+\infty}h(t) \cdot {\rm e}^{\hspace{0.05cm}{-\rm j}2\pi ft}\hspace{0.15cm} {\rm d}t = \frac{1}{T} \cdot \int_{0}^{+\infty} {\rm e}^{\hspace{0.05cm}{-(\rm j}2\pi f+ {1}/{T}) t}\hspace{0.15cm} | + | :$$H(f) = \int_{-\infty}^{+\infty}h(t) \cdot {\rm e}^{\hspace{0.05cm}{-\rm j}2\pi ft}\hspace{0.15cm} {\rm d}t = \frac{1}{T} \cdot \int_{0}^{+\infty} {\rm e}^{\hspace{0.05cm}{-(\rm j}2\pi f+ {1}/{T}) t}\hspace{0.15cm} |
{\rm d}t.$$ | {\rm d}t.$$ | ||
| − | + | *Integration leads to the result: | |
| − | $$H(f) = \left[ \frac{-1/T}{{\rm j}2\pi f+{1}/{T}} \cdot {\rm e}^{\hspace{0.05cm}{-(\rm j}2\pi f+ {1}/{T}) | + | :$$H(f) = \left[ \frac{-1/T}{{\rm j}2\pi f+{1}/{T}} \cdot {\rm e}^{\hspace{0.05cm}{-(\rm j}2\pi f+ {1}/{T}) |
t}\right]_{0}^{\infty}= \frac{1}{1+{\rm j} \cdot 2\pi fT}.$$ | t}\right]_{0}^{\infty}= \frac{1}{1+{\rm j} \cdot 2\pi fT}.$$ | ||
| − | + | *At frequency $f = 0$ the frequency response has the value $H(f = 0) \; \underline{= 1}$. | |
| − | '''2 | + | |
| − | $$H(f) = \frac{1}{1+(2\pi fT)^2} -{\rm j} \cdot \frac{2\pi fT}{1+(2\pi fT)^2}.$$ | + | '''(2)''' This frequency response can also be written with real and imaginary parts as follows: |
| − | + | :$$H(f) = \frac{1}{1+(2\pi fT)^2} -{\rm j} \cdot \frac{2\pi fT}{1+(2\pi fT)^2}.$$ | |
| − | $$h(t=0)=2 \cdot \int_{ 0 }^{ \infty } \frac{1}{1+(2\pi fT)^2} \hspace{0.1cm}{\rm | + | *The impulse response at time $t = 0$ is equal to the integral over $H(f)$. |
| + | *Since the imaginary part is odd only the real part has to be integrated over. | ||
| + | *Using the symmetry property one obtains: | ||
| + | :$$h(t=0)=2 \cdot \int_{ 0 }^{ \infty } \frac{1}{1+(2\pi fT)^2} \hspace{0.1cm}{\rm | ||
d}f = \frac{1}{\pi T} \cdot \int_{ 0 }^{ \infty } \frac{1}{1+x^2} \hspace{0.1cm}{\rm d}x .$$ | d}f = \frac{1}{\pi T} \cdot \int_{ 0 }^{ \infty } \frac{1}{1+x^2} \hspace{0.1cm}{\rm d}x .$$ | ||
| − | + | *Using the given definite integral with the result $π/2$ the following is obtained: | |
| − | $$h(t=0)= \frac{1}{2 T} \hspace{0.15cm}\underline{= {\rm 500\cdot 1/s}}.$$ | + | :$$h(t=0)= \frac{1}{2 T} \hspace{0.15cm}\underline{= {\rm 500\cdot 1/s}}.$$ |
| − | + | *The result shows that the impulse response at $t = 0$ is equal to the mean value of the left-hand and right-hand limits. | |
| + | |||
| − | '''3 | + | '''(3)''' The amplitude response in this task or in general with the 3dB cut-off frequency $f_{\rm G}$ is: |
| − | $$|H(f)| = \frac{1}{\sqrt{1+(2\pi fT)^2}} = \frac{1}{\sqrt{1+(f/f_{\rm G})^2}}.$$ | + | :$$|H(f)| = \frac{1}{\sqrt{1+(2\pi fT)^2}} = \frac{1}{\sqrt{1+(f/f_{\rm G})^2}}.$$ |
| − | + | *By comparing the coefficients one obtains: | |
| − | $$f_{\rm G} = | + | :$$f_{\rm G} = \frac{1}{2\pi T} \hspace{0.15cm}\underline{= {\rm 159 \hspace{0.1cm} Hz}}.$$ |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''(4)''' <u>The first statement</u> is correct: | |
| − | $$y(t) = K \cdot \cos( 2 \pi f_{\rm G} t - 45^{\circ}).$$ | + | *Due to $h(t) = 0$ for $t < 0$: The system is indeed causal. It is a <u>low-pass filter of first order</u>. |
| − | + | *In contrast, a high-pass filter would have to satisfy the following condition: | |
| + | :$$H(f = 0) = \int_{-\infty}^{+\infty}h(t) \hspace{0.15cm}{\rm d}t = 0.$$ | ||
| + | *$H(f)$ is a complex function. The phase response is (see [[Aufgaben:Exercise_1.1Z:_Low-Pass_Filter_of_1st_and_2nd_Order|Exercise 1.1Z]]): | ||
| + | :$$b(f) = \arctan {f}/{f_{\rm G}}.$$ | ||
| + | *For the frequency $f = f_{\rm G}$ one obtains $b(f = f_{\rm G}) = π/4 = 45^\circ$. | ||
| + | *If a cosine signal of frequency $f = f_{\rm G}$ is applied ot the input, the output signal is given by: | ||
| + | :$$y(t) = K \cdot \cos( 2 \pi f_{\rm G} t - 45^{\circ}).$$ | ||
| + | *This signal is a harmonic oscillation but not a cosine signal. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 81: | Line 104: | ||
| − | [[Category: | + | [[Category:Linear and Time-Invariant Systems: Exercises|^1.2 System Description in Time Domain^]] |
Latest revision as of 18:17, 18 July 2021
The impulse response $h(t)$ of an LTI system, which
- is identically zero for all times $t < 0$,
- changes abruptly at time $t > 0$, and
- decreases for $t > 0$ according to an exponential function:
- $$h(t) = {1}/{T} \cdot {\rm e}^{-t/T},$$ was measured.
Let the parameter be $T = 1 \hspace{0.15cm} \rm ms$. In the subtask (3) the 3dB cut-off frequency $f_{\rm G}$ is to be determined, which is (implicitly) defined as follows:
- $$|H(f = f_{\rm G})| = {1}/{\sqrt{2}} \cdot|H(f = 0)| .$$
Please note:
- The exercise belongs to the chapter System Description in Time Domain.
- The following definite integral is given:
- $$\int_{ 0 }^{ \infty } \frac{1}{1+x^2} \hspace{0.1cm}{\rm d}x = {\pi}/{2} .$$
Questions
Solution
(1) The frequency response $H(f)$ is the Fourier transform of $h(t)$:
- $$H(f) = \int_{-\infty}^{+\infty}h(t) \cdot {\rm e}^{\hspace{0.05cm}{-\rm j}2\pi ft}\hspace{0.15cm} {\rm d}t = \frac{1}{T} \cdot \int_{0}^{+\infty} {\rm e}^{\hspace{0.05cm}{-(\rm j}2\pi f+ {1}/{T}) t}\hspace{0.15cm} {\rm d}t.$$
- Integration leads to the result:
- $$H(f) = \left[ \frac{-1/T}{{\rm j}2\pi f+{1}/{T}} \cdot {\rm e}^{\hspace{0.05cm}{-(\rm j}2\pi f+ {1}/{T}) t}\right]_{0}^{\infty}= \frac{1}{1+{\rm j} \cdot 2\pi fT}.$$
- At frequency $f = 0$ the frequency response has the value $H(f = 0) \; \underline{= 1}$.
(2) This frequency response can also be written with real and imaginary parts as follows:
- $$H(f) = \frac{1}{1+(2\pi fT)^2} -{\rm j} \cdot \frac{2\pi fT}{1+(2\pi fT)^2}.$$
- The impulse response at time $t = 0$ is equal to the integral over $H(f)$.
- Since the imaginary part is odd only the real part has to be integrated over.
- Using the symmetry property one obtains:
- $$h(t=0)=2 \cdot \int_{ 0 }^{ \infty } \frac{1}{1+(2\pi fT)^2} \hspace{0.1cm}{\rm d}f = \frac{1}{\pi T} \cdot \int_{ 0 }^{ \infty } \frac{1}{1+x^2} \hspace{0.1cm}{\rm d}x .$$
- Using the given definite integral with the result $π/2$ the following is obtained:
- $$h(t=0)= \frac{1}{2 T} \hspace{0.15cm}\underline{= {\rm 500\cdot 1/s}}.$$
- The result shows that the impulse response at $t = 0$ is equal to the mean value of the left-hand and right-hand limits.
(3) The amplitude response in this task or in general with the 3dB cut-off frequency $f_{\rm G}$ is:
- $$|H(f)| = \frac{1}{\sqrt{1+(2\pi fT)^2}} = \frac{1}{\sqrt{1+(f/f_{\rm G})^2}}.$$
- By comparing the coefficients one obtains:
- $$f_{\rm G} = \frac{1}{2\pi T} \hspace{0.15cm}\underline{= {\rm 159 \hspace{0.1cm} Hz}}.$$
(4) The first statement is correct:
- Due to $h(t) = 0$ for $t < 0$: The system is indeed causal. It is a low-pass filter of first order.
- In contrast, a high-pass filter would have to satisfy the following condition:
- $$H(f = 0) = \int_{-\infty}^{+\infty}h(t) \hspace{0.15cm}{\rm d}t = 0.$$
- $H(f)$ is a complex function. The phase response is (see Exercise 1.1Z):
- $$b(f) = \arctan {f}/{f_{\rm G}}.$$
- For the frequency $f = f_{\rm G}$ one obtains $b(f = f_{\rm G}) = π/4 = 45^\circ$.
- If a cosine signal of frequency $f = f_{\rm G}$ is applied ot the input, the output signal is given by:
- $$y(t) = K \cdot \cos( 2 \pi f_{\rm G} t - 45^{\circ}).$$
- This signal is a harmonic oscillation but not a cosine signal.