Difference between revisions of "Aufgaben:Exercise 1.1Z: Sum of Two Ternary Signals"
From LNTwww
| (21 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Some_Basic_Definitions}} |
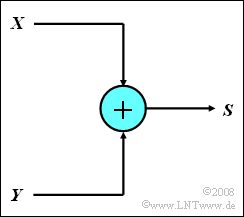
| − | [[File:P_ID146__Sto_Z1_1.png|right|]] | + | [[File:P_ID146__Sto_Z1_1.png|right|framed|Sum $S$ of two <br>ternary signals $X$ and $Y$]] |
| − | + | Let two three-stage message sources $X$ and $Y$ be given, whose output signals can only assume the values $-1$, $0$ and $+1$ respectively. The signal sources are statistically independent of each other. | |
| − | |||
| − | ''' | + | *A simple circuit now forms the sum signal $S = X + Y$. |
| − | === | + | *At the signal source $X$, the values $-1$, $0$ and $+1$ occur with equal probability. |
| + | *For source $Y$, the signal value $0$ is twice as likely as the other two values $-1$ and $+1$, respectively. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hints: | ||
| + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Einige_grundlegende_Definitionen | Some basic definitions of probability theory]]. | ||
| + | |||
| + | *Solve the subtasks '''(3)''' and '''(4)''' according to the classical definition. | ||
| + | *Nevertheless, consider the different occurrence frequencies of the signal $Y$. | ||
| + | *The topic of this section is illustrated with examples in the (German language) learning video <br>[[Klassische_Definition_der_Wahrscheinlickeit_(Lernvideo)|Klassische Definition der Wahrscheinlichkeit]] $\Rightarrow$ "Classical definition of probability". | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What are the probabilities of occurrence of the signal values of $Y$? What is the probability that $Y = 0$ ? |
|type="{}"} | |type="{}"} | ||
| − | $Pr(Y=0) = $ { 0.5 3% } | + | ${\rm Pr}(Y=0) \ = \ $ { 0.5 3% } |
| − | { | + | {How many different signal values $(I)$ can the sum signal $S$ assume? Which are these? |
|type="{}"} | |type="{}"} | ||
| − | $ I = $ { 5 3% } | + | $ I \ = \ $ { 5 3% } |
| − | { | + | {What are the probabilities of the values determined in subtask '''(2)'''? How probable is the maximum value $S_{\rm max}$? |
|type="{}"} | |type="{}"} | ||
| − | $ Pr(S = S_\max ) = $ { 0.0833 3% } | + | $ {\rm Pr}(S = S_{\rm max} ) \ = \ $ { 0.0833 3% } |
| − | { | + | {How do the probabilities change, if now instead of the sum the difference $D = X - Y$ is considered? Give reasons for your answer. |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The probabilities remain the same. |
| − | - | + | - The probabilities change. How do they change? |
| Line 34: | Line 50: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' Since the probabilities of $ \pm 1$ are the same and ${\rm Pr}(Y = 0) = 2 \cdot {\rm Pr}(Y = 1)$ holds, we get: | |
| + | |||
| + | :$${\rm Pr}(Y = 1) + {\rm Pr}(Y = 0) + {\rm Pr}(Y = -1) = 1/2 \cdot {\rm Pr}(Y = 0) + {\rm Pr}(Y = 0) + 1/2\cdot {\rm Pr}(Y = 0) = 1\hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm Pr}(Y = 0)\;\underline { = 0.5}. $$ | ||
| − | |||
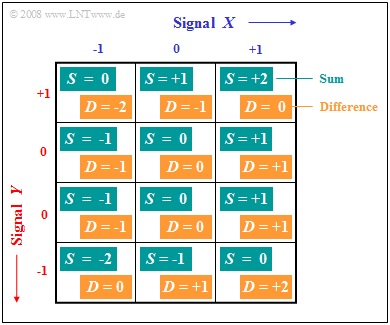
| − | $ \ | + | [[File:EN_Sto_Z1_1_c_neu.png|right|frame|400px|Sum and difference of ternary random variables]] |
| + | '''(2)''' $S$ can take a total of $\underline {I =5}$ values, namely $0$, $\pm 1$ and $\pm 2$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''(3)''' Since $Y$ is not equally distributed, one cannot (actually) apply the "Classical Definition of Probability" here. | |
| − | $ | + | *However, if we divide $Y$ into four ranges according to the graph, assigning two of the ranges to the event $Y = 0$, we can still proceed according to the classical definition. |
| + | *One then obtains: | ||
| − | $Pr(S = +1) = \ | + | :$${\rm Pr}(S = 0) = {4}/{12} = {1}/{3},$$ |
| + | :$${\rm Pr}(S = +1) = {\rm Pr}(S = -1) ={3}/{12} = {1}/{4},$$ | ||
| + | :$${\rm Pr}(S = +2) = {\rm Pr}(S = -2) ={1}/{12}$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm}{\rm Pr}(S = S_{\rm max}) = {\rm Pr}(S = +2) =1/12 \;\underline {= 0.0833}.$$ | ||
| − | |||
| − | $ | + | '''(4)''' It is also evident from the graph that the difference signal $D$ and the sum signal $S$ take the same values with equal probabilities. |
| − | + | *This was to be expected, since ${\rm Pr}(Y = +1) ={\rm Pr}(Y = -1)$ is given ⇒ <u>Proposed solution 1</u>. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Theory of Stochastic Signals: Exercises|^1.1 Some Basic Definitions |
^]] | ^]] | ||
Latest revision as of 16:42, 26 November 2021
Sum $S$ of two
ternary signals $X$ and $Y$
ternary signals $X$ and $Y$
Let two three-stage message sources $X$ and $Y$ be given, whose output signals can only assume the values $-1$, $0$ and $+1$ respectively. The signal sources are statistically independent of each other.
- A simple circuit now forms the sum signal $S = X + Y$.
- At the signal source $X$, the values $-1$, $0$ and $+1$ occur with equal probability.
- For source $Y$, the signal value $0$ is twice as likely as the other two values $-1$ and $+1$, respectively.
Hints:
- The exercise belongs to the chapter Some basic definitions of probability theory.
- Solve the subtasks (3) and (4) according to the classical definition.
- Nevertheless, consider the different occurrence frequencies of the signal $Y$.
- The topic of this section is illustrated with examples in the (German language) learning video
Klassische Definition der Wahrscheinlichkeit $\Rightarrow$ "Classical definition of probability".
Questions
Solution
(1) Since the probabilities of $ \pm 1$ are the same and ${\rm Pr}(Y = 0) = 2 \cdot {\rm Pr}(Y = 1)$ holds, we get:
- $${\rm Pr}(Y = 1) + {\rm Pr}(Y = 0) + {\rm Pr}(Y = -1) = 1/2 \cdot {\rm Pr}(Y = 0) + {\rm Pr}(Y = 0) + 1/2\cdot {\rm Pr}(Y = 0) = 1\hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm Pr}(Y = 0)\;\underline { = 0.5}. $$
Sum and difference of ternary random variables
(2) $S$ can take a total of $\underline {I =5}$ values, namely $0$, $\pm 1$ and $\pm 2$.
(3) Since $Y$ is not equally distributed, one cannot (actually) apply the "Classical Definition of Probability" here.
- However, if we divide $Y$ into four ranges according to the graph, assigning two of the ranges to the event $Y = 0$, we can still proceed according to the classical definition.
- One then obtains:
- $${\rm Pr}(S = 0) = {4}/{12} = {1}/{3},$$
- $${\rm Pr}(S = +1) = {\rm Pr}(S = -1) ={3}/{12} = {1}/{4},$$
- $${\rm Pr}(S = +2) = {\rm Pr}(S = -2) ={1}/{12}$$
- $$\Rightarrow \hspace{0.3cm}{\rm Pr}(S = S_{\rm max}) = {\rm Pr}(S = +2) =1/12 \;\underline {= 0.0833}.$$
(4) It is also evident from the graph that the difference signal $D$ and the sum signal $S$ take the same values with equal probabilities.
- This was to be expected, since ${\rm Pr}(Y = +1) ={\rm Pr}(Y = -1)$ is given ⇒ Proposed solution 1.
