Difference between revisions of "Aufgaben:Exercise 3.6Z: Complex Exponential Function"
From LNTwww
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Signaldarstellung/Gesetzmäßigkeiten der Fouriertransformation }} right| In Zusammenhang mit Ba…“) |
m (Text replacement - "bandpass" to "band-pass") |
||
| (31 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Signal_Representation/Fourier_Transform_Laws |
}} | }} | ||
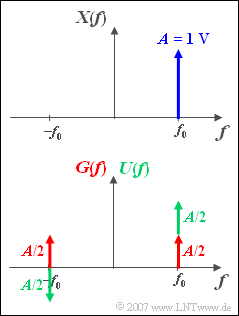
| − | [[File:P_ID518__Sig_Z_3_6_neu.png|right|]] | + | [[File:P_ID518__Sig_Z_3_6_neu.png|right|frame|Splitting the complex exponential function in the spectral domain]] |
| − | In | + | In connection with [[Signal_Representation/Differences_and_Similarities_of_LP_and_BP_Signals|"band-pass systems"]] , one-sided spectra are often used. In the graphic you see such a one-sided spectral function ${X(f)}$, which results in a complex time signal ${x(t)}$. |
| − | In | + | In the sketch below, ${X(f)}$ is split into an even component ${G(f)}$ – with respect to the frequency – and an odd component ${U(f)}$. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | |
| + | |||
| + | ''Hints:'' | ||
| + | *This exercise belongs to the chapter [[Signal_Representation/Fourier_Transform_Theorems|Fourier Transform Theorems]]. | ||
| + | *For the first two sub-tasks use the signal parameters $A = 1\, \text{V}$ and $f_0 = 125 \,\text{kHz}$. | ||
| + | *The [[Signal_Representation/Fourier_Transform_Theorems#Shifting_Theorem|Shifting Theorem]] and the [[Signal_Representation/Fourier_Transform_Theorems#Assignment_Theorem|Assignment Theorem]] – are illustrated with examples in the (German language) learning video<br> [[Gesetzmäßigkeiten_der_Fouriertransformation_(Lernvideo)|Gesetzmäßigkeiten der Fouriertransformation]] ⇒ "Regularities to the Fourier transform". | ||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the time function $g(t)$ that fits $G(f)$? How large is $g(t = 1 \, µ \text {s})$? |
|type="{}"} | |type="{}"} | ||
| − | $\text{Re}[g(t = 1 \ | + | $\text{Re}\big[g(t = 1 \, µ \text {s})\big] \ = \ $ { 0.707 3% } $\text{V}$ |
| − | $\text{Im}[g(t = 1 \ | + | $\text{Im}\big[g(t = 1 \, µ \text {s})\big]\ = \ $ { 0. } $\text{V}$ |
| − | { | + | {What is the time function $u(t)$ that fits $U(f)$? What is the value of $u(t = 1 \, µ \text {s})$? |
|type="{}"} | |type="{}"} | ||
| − | $\text{Re}[u(t = 1 \ | + | $\text{Re}\big[u(t = 1 \, µ \text {s})\big]\ = \ $ { 0. } $\text{V}$ |
| − | $\text{Im}[u(t = 1 \ | + | $\text{Im}\big[u(t = 1 \, µ \text {s})\big]\ = \ $ { 0.707 3% } $\text{V}$ |
| − | { | + | {Which of the statements are true regarding the signal $x(t)$ ? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The signal is $x(t) = A \cdot {\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi\hspace{0.05cm}\cdot \hspace{0.05cm} f_0 \hspace{0.05cm}\cdot \hspace{0.05cm}t}$. |
| − | - In | + | - In the complex plane $x(t)$ rotates clockwise. |
| − | + $ | + | + In the complex plane $x(t)$ rotates counterclockwise. |
| − | - | + | - One microsecond is needed for one rotation. |
| Line 45: | Line 48: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' $G(f)$ is the spectral function of a cosine signal with period $T_0 = 1/f_0 = 8 \, µ\text {s}$: |
:$$g( t ) = A \cdot \cos ( {2{\rm{\pi }}f_0 t} ).$$ | :$$g( t ) = A \cdot \cos ( {2{\rm{\pi }}f_0 t} ).$$ | ||
| − | + | At $t = 1 \, µ\text {s}$ the signal value is equal to $A \cdot \cos(\pi /4)$: | |
| + | *The real part is $\text{Re}[g(t = 1 \, µ \text {s})] = \;\underline{0.707\, \text{V}}$, | ||
| + | *The imaginary part is $\text{Im}[g(t = 1 \, µ \text {s})] = \;\underline{0.}$ | ||
| + | |||
| + | |||
| − | '''2 | + | '''(2)''' Starting from the Fourier correspondence |
| − | :$$A \cdot {\rm \delta} ( f )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, A$$ | + | :$$A \cdot {\rm \delta} ( f )\ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ \ A$$ |
| − | + | is obtained by applying the shifting theorem twice (in the frequency domain): | |
| − | :$$U( f ) = | + | :$$U( f ) = {A}/{2} \cdot \delta ( {f - f_0 } ) - {A}/{2} \cdot \delta ( {f + f_0 } )\ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ \ u( t ) = {A}/{2} \cdot \left( {{\rm{e}}^{{\rm{j}}\hspace{0.05cm}\cdot \hspace{0.05cm}2{\rm{\pi }}\hspace{0.05cm}\cdot \hspace{0.05cm}f_0\hspace{0.05cm}\cdot \hspace{0.05cm} t} - {\rm{e}}^{{\rm{ - j}}\hspace{0.05cm}\cdot \hspace{0.05cm}2{\rm{\pi }}\hspace{0.05cm}\cdot \hspace{0.05cm}f_0 \hspace{0.05cm}\cdot \hspace{0.05cm}t} } \right).$$ |
| − | + | *According to [[Signal_Representation/Calculating_With_Complex_Numbers#Representation_by_magnitude_and_phase|Euler's theorem]] , this can also be written. | |
:$$u( t ) = {\rm{j}} \cdot A \cdot \sin ( {2{\rm{\pi }}f_0 t} ).$$ | :$$u( t ) = {\rm{j}} \cdot A \cdot \sin ( {2{\rm{\pi }}f_0 t} ).$$ | ||
| − | + | :*The <u>real part of this signal is always zero</u>. | |
| + | :*At $t = 1 \, µ\text {s}$ the following applies to the imaginary part: $\text{Im}[g(t = 1 \, µ \text {s})] = \;\underline{0.707\, \text{V}}$. | ||
| + | |||
| + | |||
| − | '''3 | + | '''(3)''' Because $X(f) = G(f) + U(f)$ also holds: |
:$$x(t) = g(t) + u(t) = A \cdot \cos ( {2{\rm{\pi }}f_0 t} ) + {\rm{j}} \cdot A \cdot \sin( {2{\rm{\pi }}f_0 t} ).$$ | :$$x(t) = g(t) + u(t) = A \cdot \cos ( {2{\rm{\pi }}f_0 t} ) + {\rm{j}} \cdot A \cdot \sin( {2{\rm{\pi }}f_0 t} ).$$ | ||
| − | + | This result can be summarised by "Euler's theorem" as follows: | |
| − | :$$x(t) = A \cdot {\rm{e}}^{{\rm{j}}2{\rm{\pi }}f_0 t} .$$ | + | :$$x(t) = A \cdot {\rm{e}}^{{\rm{j}}\hspace{0.05cm}\cdot \hspace{0.05cm}2{\rm{\pi }}\hspace{0.05cm}\cdot \hspace{0.05cm}f_0 \hspace{0.05cm}\cdot \hspace{0.05cm}t} .$$ |
| − | + | The given <u>alternatives 1 and 3</u> are correct: | |
| + | *The signal rotates in the complex plane in a mathematically positive direction, i.e. counterclockwise. | ||
| + | *For one rotation, the "pointer" needs the period $T_0 = 1/f_0 = 8 \, µ\text {s}$. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
| − | [[Category: | + | [[Category:Signal Representation: Exercises|^3.3 Fourier Transform Theorems^]] |
Latest revision as of 16:12, 3 May 2021
In connection with "band-pass systems" , one-sided spectra are often used. In the graphic you see such a one-sided spectral function ${X(f)}$, which results in a complex time signal ${x(t)}$.
In the sketch below, ${X(f)}$ is split into an even component ${G(f)}$ – with respect to the frequency – and an odd component ${U(f)}$.
Hints:
- This exercise belongs to the chapter Fourier Transform Theorems.
- For the first two sub-tasks use the signal parameters $A = 1\, \text{V}$ and $f_0 = 125 \,\text{kHz}$.
- The Shifting Theorem and the Assignment Theorem – are illustrated with examples in the (German language) learning video
Gesetzmäßigkeiten der Fouriertransformation ⇒ "Regularities to the Fourier transform".
Questions
Solution
(1) $G(f)$ is the spectral function of a cosine signal with period $T_0 = 1/f_0 = 8 \, µ\text {s}$:
- $$g( t ) = A \cdot \cos ( {2{\rm{\pi }}f_0 t} ).$$
At $t = 1 \, µ\text {s}$ the signal value is equal to $A \cdot \cos(\pi /4)$:
- The real part is $\text{Re}[g(t = 1 \, µ \text {s})] = \;\underline{0.707\, \text{V}}$,
- The imaginary part is $\text{Im}[g(t = 1 \, µ \text {s})] = \;\underline{0.}$
(2) Starting from the Fourier correspondence
- $$A \cdot {\rm \delta} ( f )\ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ \ A$$
is obtained by applying the shifting theorem twice (in the frequency domain):
- $$U( f ) = {A}/{2} \cdot \delta ( {f - f_0 } ) - {A}/{2} \cdot \delta ( {f + f_0 } )\ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ \ u( t ) = {A}/{2} \cdot \left( {{\rm{e}}^{{\rm{j}}\hspace{0.05cm}\cdot \hspace{0.05cm}2{\rm{\pi }}\hspace{0.05cm}\cdot \hspace{0.05cm}f_0\hspace{0.05cm}\cdot \hspace{0.05cm} t} - {\rm{e}}^{{\rm{ - j}}\hspace{0.05cm}\cdot \hspace{0.05cm}2{\rm{\pi }}\hspace{0.05cm}\cdot \hspace{0.05cm}f_0 \hspace{0.05cm}\cdot \hspace{0.05cm}t} } \right).$$
- According to Euler's theorem , this can also be written.
- $$u( t ) = {\rm{j}} \cdot A \cdot \sin ( {2{\rm{\pi }}f_0 t} ).$$
- The real part of this signal is always zero.
- At $t = 1 \, µ\text {s}$ the following applies to the imaginary part: $\text{Im}[g(t = 1 \, µ \text {s})] = \;\underline{0.707\, \text{V}}$.
(3) Because $X(f) = G(f) + U(f)$ also holds:
- $$x(t) = g(t) + u(t) = A \cdot \cos ( {2{\rm{\pi }}f_0 t} ) + {\rm{j}} \cdot A \cdot \sin( {2{\rm{\pi }}f_0 t} ).$$
This result can be summarised by "Euler's theorem" as follows:
- $$x(t) = A \cdot {\rm{e}}^{{\rm{j}}\hspace{0.05cm}\cdot \hspace{0.05cm}2{\rm{\pi }}\hspace{0.05cm}\cdot \hspace{0.05cm}f_0 \hspace{0.05cm}\cdot \hspace{0.05cm}t} .$$
The given alternatives 1 and 3 are correct:
- The signal rotates in the complex plane in a mathematically positive direction, i.e. counterclockwise.
- For one rotation, the "pointer" needs the period $T_0 = 1/f_0 = 8 \, µ\text {s}$.