Difference between revisions of "Aufgaben:Exercise 1.6Z: Ergodic Probabilities"
From LNTwww
m (Nabil verschob die Seite Zusatzaufgaben:1.6 Ergodische Wahrscheinlichkeiten nach 1.6Z Ergodische Wahrscheinlichkeiten) |
|||
| (15 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Markov_Chains}} |
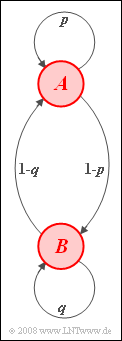
| − | [[File:P_ID452__Sto_Z_1_6.png|right|]] | + | [[File:P_ID452__Sto_Z_1_6.png|right|frame|Markov chain with $A$, $B$]] |
| − | + | We consider a homogeneous stationary first-order Markov chain with events $A$ and $B$ and transition probabilities corresponding to the adjacent Markov diagram: | |
| − | + | For subtasks '''(1)''' to '''(4)''', assume: | |
| − | * | + | *Event $A$ is followed by $A$ and $B$ with equal probability. |
| − | * | + | *After $B$: The event $A$ is twice as likely as $B$. |
| − | |||
| + | From subtask '''(5)''' on, $p$ and $q$ are free parameters, while the ergodic probabilities ${\rm Pr}(A) = 2/3$ and ${\rm Pr}(B) = 1/3$ are fixed. | ||
| − | |||
| − | === | + | |
| + | |||
| + | |||
| + | Hints: | ||
| + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Markov_Chains|Markov Chains]]. | ||
| + | |||
| + | *You can check your results with the (German language) interactive SWF applet | ||
| + | : [[Applets:Markovketten|Ereigniswahrscheinlichkeiten einer Markov-Kette erster Ordnung]] ⇒ "Event Probabilities of a First Order Markov Chain". | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What are the transition probabilities $p$ and $q$? |
|type="{}"} | |type="{}"} | ||
| − | $p$ | + | $p \ = \ $ { 0.5 3% } |
| − | $q$ | + | $q \ = \ $ { 0.333 3% } |
| − | { | + | {Calculate the ergodic probabilities. |
|type="{}"} | |type="{}"} | ||
| − | $Pr(A)$ | + | ${\rm Pr}(A) \ = \ $ { 0.571 3% } |
| − | $Pr(B)$ | + | ${\rm Pr}(B) \ = \ $ { 0.429 3% } |
| − | { | + | {What is the conditional probability that event $B$ occurs if event $A$ occurred two steps before? |
|type="{}"} | |type="{}"} | ||
| − | $Pr( | + | ${\rm Pr}(B_{\nu}\hspace{0.05cm}|\hspace{0.05cm}A_{\nu-2})\ = \ $ { 0.417 3% } |
| − | { | + | {What is the inferential probability that event $A$ occurred two steps before, when event $B$ currently occurs? |
|type="{}"} | |type="{}"} | ||
| − | $Pr(A_\ | + | ${\rm Pr}(A_{\nu-2}\hspace{0.05cm}|\hspace{0.05cm}B_{\nu})\ = \ $ { 0.556 3% } |
| − | { | + | {Let now $p = 1/2$ and ${\rm Pr}(A) = 2/3$. Which value results for $q$? |
|type="{}"} | |type="{}"} | ||
| − | $q$ | + | $q\ = \ $ { 0. } |
| − | { | + | {How must the parameters be chosen so that the sequence elements of the Markov chain are statistically independent and additionally ${\rm Pr}(A) = 2/3$ ? |
|type="{}"} | |type="{}"} | ||
| − | $p$ | + | $p \ = \ $ { 0.667 3% } |
| − | $q$ | + | $q \ = \ $ { 0.333 3% } |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' According to the instruction, $p = 1 - p$ ⇒ $\underline{p =0.500}$ and $q = (1 - q)/2$, ⇒ $\underline{q =0.333}$ holds. | |
| − | + | ||
| + | |||
| + | |||
| + | '''(2)''' For the event probability of $A$ holds: | ||
:$${\rm Pr}(A) = \frac{{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B)}{{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B)+{\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A)} = \frac{1-q}{1-q+1-p} = \frac{2/3}{2/3 + 1/2}= \frac{4}{7} \hspace{0.15cm}\underline {\approx0.571}.$$ | :$${\rm Pr}(A) = \frac{{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B)}{{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B)+{\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A)} = \frac{1-q}{1-q+1-p} = \frac{2/3}{2/3 + 1/2}= \frac{4}{7} \hspace{0.15cm}\underline {\approx0.571}.$$ | ||
| − | + | *This gives ${\rm Pr}(B)= 1 - {\rm Pr}(A) = 3/7 \hspace{0.15cm}\underline {\approx 0.429}$. | |
| − | + | ||
| − | :$${\rm Pr}(B_{\nu} \hspace{0.05cm} | \hspace{0.05cm}A_{\nu -2}) = {\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}A) \hspace{0.05cm} \cdot \hspace{0.05cm}{\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) \hspace{0.15cm} +\hspace{0.15cm} {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) \hspace{0.05cm} \cdot \hspace{0.05cm}{\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}B) | + | |
| − | = | + | |
| − | + | ||
| + | '''(3)''' No statement is made about the time $\nu-1$ . | ||
| + | *At this time $A$ or $B$ may have occurred. Therefore holds: | ||
| + | :$${\rm Pr}(B_{\nu} \hspace{0.05cm} | \hspace{0.05cm}A_{\nu -2}) = {\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}A) \hspace{0.05cm} \cdot \hspace{0.05cm}{\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) \hspace{0.15cm} +\hspace{0.15cm} {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) \hspace{0.05cm} \cdot \hspace{0.05cm}{\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}B) = p \hspace{0.1cm} \cdot \hspace{0.1cm} (1-p) + q \hspace{0.1cm} \cdot \hspace{0.1cm} (1-p) | ||
| + | = {5}/{12} \hspace{0.15cm}\underline {\approx 0.417}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' According to Bayes' theorem: | ||
:$${\rm Pr}(A_{\nu -2} \hspace{0.05cm} | \hspace{0.05cm}B_{\nu}) = \frac{{\rm Pr}(B_{\nu} \hspace{0.05cm} | \hspace{0.05cm}A_{\nu -2}) \cdot {\rm Pr}(A_{\nu -2} ) }{{\rm Pr}(B_{\nu}) } = \frac{5/12 \cdot 4/7 }{3/7 } | :$${\rm Pr}(A_{\nu -2} \hspace{0.05cm} | \hspace{0.05cm}B_{\nu}) = \frac{{\rm Pr}(B_{\nu} \hspace{0.05cm} | \hspace{0.05cm}A_{\nu -2}) \cdot {\rm Pr}(A_{\nu -2} ) }{{\rm Pr}(B_{\nu}) } = \frac{5/12 \cdot 4/7 }{3/7 } | ||
| − | = | + | = {5}/{9} \hspace{0.15cm}\underline {\approx 0.556}.$$ |
| − | : | + | Reasoning: |
| − | + | *The probability ${\rm Pr}(B_{\nu}\hspace{0.05cm}|\hspace{0.05cm}A_{\nu-2})= 5/12$ has already been calculated in subsection '''(3)'''. | |
| + | *Due to stationarity, ${\rm Pr}(A_{\nu-2})= {\rm Pr}(A) = 4/7$ and ${\rm Pr}(B_{\nu})= {\rm Pr}(B) = 3/7$ holds. | ||
| + | *Thus, the value of $5/9$ is obtained for the sought inference probability according to the above equation. | ||
| + | |||
| + | |||
| + | |||
| + | '''(5)''' According to subtask '''(2)''' with ${p =1/2}$ for the probability of $A$ in general: | ||
:$${\rm Pr}(A) = \frac{1-q}{1.5 -q}.$$ | :$${\rm Pr}(A) = \frac{1-q}{1.5 -q}.$$ | ||
| − | + | *Thus from $ {\rm Pr}(A) = 2/3$ follows $\underline{q =0}$. | |
| − | + | ||
| + | |||
| + | |||
| + | '''(6)''' In the case of statistical independence, for example, it must hold: | ||
:$${{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}A)} = {{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B)} = {{\rm Pr}(A)}.$$ | :$${{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}A)} = {{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B)} = {{\rm Pr}(A)}.$$ | ||
| − | + | *From this follows $p = {\rm Pr}(A) \hspace{0.15cm}\underline {= 2/3}$ and accordingly $q = 1-p \hspace{0.15cm}\underline {= 1/3}$. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Theory of Stochastic Signals: Exercises|^1.4 Markov Chains |
^]] | ^]] | ||
Latest revision as of 18:07, 1 December 2021
We consider a homogeneous stationary first-order Markov chain with events $A$ and $B$ and transition probabilities corresponding to the adjacent Markov diagram:
For subtasks (1) to (4), assume:
- Event $A$ is followed by $A$ and $B$ with equal probability.
- After $B$: The event $A$ is twice as likely as $B$.
From subtask (5) on, $p$ and $q$ are free parameters, while the ergodic probabilities ${\rm Pr}(A) = 2/3$ and ${\rm Pr}(B) = 1/3$ are fixed.
Hints:
- The exercise belongs to the chapter Markov Chains.
- You can check your results with the (German language) interactive SWF applet
- Ereigniswahrscheinlichkeiten einer Markov-Kette erster Ordnung ⇒ "Event Probabilities of a First Order Markov Chain".
Questions
Solution
(1) According to the instruction, $p = 1 - p$ ⇒ $\underline{p =0.500}$ and $q = (1 - q)/2$, ⇒ $\underline{q =0.333}$ holds.
(2) For the event probability of $A$ holds:
- $${\rm Pr}(A) = \frac{{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B)}{{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B)+{\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A)} = \frac{1-q}{1-q+1-p} = \frac{2/3}{2/3 + 1/2}= \frac{4}{7} \hspace{0.15cm}\underline {\approx0.571}.$$
- This gives ${\rm Pr}(B)= 1 - {\rm Pr}(A) = 3/7 \hspace{0.15cm}\underline {\approx 0.429}$.
(3) No statement is made about the time $\nu-1$ .
- At this time $A$ or $B$ may have occurred. Therefore holds:
- $${\rm Pr}(B_{\nu} \hspace{0.05cm} | \hspace{0.05cm}A_{\nu -2}) = {\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}A) \hspace{0.05cm} \cdot \hspace{0.05cm}{\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) \hspace{0.15cm} +\hspace{0.15cm} {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) \hspace{0.05cm} \cdot \hspace{0.05cm}{\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}B) = p \hspace{0.1cm} \cdot \hspace{0.1cm} (1-p) + q \hspace{0.1cm} \cdot \hspace{0.1cm} (1-p) = {5}/{12} \hspace{0.15cm}\underline {\approx 0.417}.$$
(4) According to Bayes' theorem:
- $${\rm Pr}(A_{\nu -2} \hspace{0.05cm} | \hspace{0.05cm}B_{\nu}) = \frac{{\rm Pr}(B_{\nu} \hspace{0.05cm} | \hspace{0.05cm}A_{\nu -2}) \cdot {\rm Pr}(A_{\nu -2} ) }{{\rm Pr}(B_{\nu}) } = \frac{5/12 \cdot 4/7 }{3/7 } = {5}/{9} \hspace{0.15cm}\underline {\approx 0.556}.$$
Reasoning:
- The probability ${\rm Pr}(B_{\nu}\hspace{0.05cm}|\hspace{0.05cm}A_{\nu-2})= 5/12$ has already been calculated in subsection (3).
- Due to stationarity, ${\rm Pr}(A_{\nu-2})= {\rm Pr}(A) = 4/7$ and ${\rm Pr}(B_{\nu})= {\rm Pr}(B) = 3/7$ holds.
- Thus, the value of $5/9$ is obtained for the sought inference probability according to the above equation.
(5) According to subtask (2) with ${p =1/2}$ for the probability of $A$ in general:
- $${\rm Pr}(A) = \frac{1-q}{1.5 -q}.$$
- Thus from $ {\rm Pr}(A) = 2/3$ follows $\underline{q =0}$.
(6) In the case of statistical independence, for example, it must hold:
- $${{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}A)} = {{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B)} = {{\rm Pr}(A)}.$$
- From this follows $p = {\rm Pr}(A) \hspace{0.15cm}\underline {= 2/3}$ and accordingly $q = 1-p \hspace{0.15cm}\underline {= 1/3}$.