Difference between revisions of "Aufgaben:Exercise 2.2Z: Discrete Random Variables"
From LNTwww
m (Nabil verschob die Seite Zusatzaufgaben:2.2 Diskrete Zufallsgrößen nach 2.2Z Diskrete Zufallsgrößen) |
|||
| (23 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Moments_of_a_Discrete_Random_Variable |
}} | }} | ||
| − | |||
| − | |||
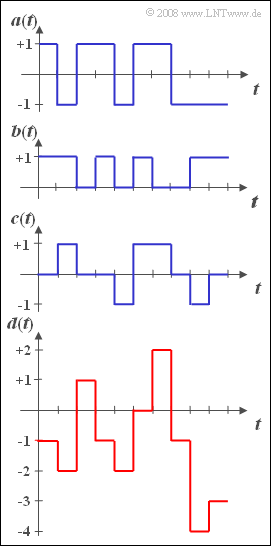
| − | : | + | [[File:P_ID84__Sto_Z_2_2.png|right|frame|Different rectangular signals]] |
| + | Let be given three discrete random variables $a$, $b$ and $c$, which are defined as the instantaneous values of the represented signals. These have the following properties: | ||
| − | + | *The random variable $a$ can take the two values $+1$ and $-1$ with equal probability. | |
| + | *The random variable $b$ is also two-point distributed, but with ${\rm Pr}(b = 1) = p$ and ${\rm Pr}(b = 0) = 1 - p$. | ||
| + | *The probabilities of the random variable $c$ be ${\rm Pr}(c = 0) = 1/2$ and ${\rm Pr}(c = +1) = Pr(c = -1) =1/4$. | ||
| + | *There are no statistical dependencies between the three random variables $a$, $b$ and $c$. | ||
| + | *Another random variable $d$ is formed from the random variables $a$, $b$ and $c$: | ||
| + | :$$d=a-2 b+c.$$ | ||
| − | + | The graph shows sections of these random variables. It can be seen that $d$ can take all integer values between $-4$ and $+2$ . | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | |
| + | Hints: | ||
| + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Momente_einer_diskreten_Zufallsgröße|Moments of a Discrete Random Variable]]. | ||
| + | *The topic of this chapter is illustrated with examples in the (German language) learning video<br> [[Momentenberechnung_bei_diskreten_Zufallsgrößen_(Lernvideo)|"Momentenberechnung bei diskreten Zufallsgrößen"]] ⇒ "Calculating Moments for Discrete-Valued Random Variables" | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | |
| + | {What is the standard deviation of the random variable $a$? | ||
|type="{}"} | |type="{}"} | ||
| − | $\sigma_a$ | + | $\sigma_a \ = \ $ { 1 3% } |
| − | { | + | {What is the standard deviation of the random variable $b$? Set $p = 0.25$. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $\sigma_b \ = \ $ { 0.433 3% } |
| − | { | + | {What is the standard deviation of the random variable $c$? |
|type="{}"} | |type="{}"} | ||
| − | $\sigma_c$ | + | $\sigma_c \ = \ $ { 0.707 3% } |
| − | { | + | {Calculate the mean $m_d$ of the random variable $d$ for $p = 0.25$. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $m_d\ = \ $ { -0.515--0.485 } |
| − | { | + | {What is the second moment value (second order moment) $m_{2d}$ of this random variable? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $m_{2d}\ = \ $ { 2.5 3% } |
| − | { | + | {What is the standard deviation $\sigma_d$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $\sigma_d\ = \ $ { 1.5 3% } |
| + | </quiz> | ||
| − | |||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' Due to the symmetry holds: | |
:$$\rm \it m_{\it a}=\rm 0; \hspace{0.5cm}\it m_{\rm 2\it a}=\rm 0.5\cdot (-1)^2 + 0.5\cdot (1)^2{ = 1}.$$ | :$$\rm \it m_{\it a}=\rm 0; \hspace{0.5cm}\it m_{\rm 2\it a}=\rm 0.5\cdot (-1)^2 + 0.5\cdot (1)^2{ = 1}.$$ | ||
| − | + | *From this one obtains with Steiner's theorem: | |
| − | :$$\it\sigma_a^{\rm 2} = \rm\sqrt{1-0^2}=1 \hspace{0.5cm} | + | :$$\it\sigma_a^{\rm 2} = \rm\sqrt{1-0^2}=1 \hspace{0.5cm}or \hspace{0.5cm}\it\sigma_a\hspace{0.15cm} \underline{=\rm 1}.$$ |
| + | |||
| + | |||
| + | '''(2)''' In general, for the $k$–th order moment: | ||
| + | :$$ m_{k}=(1-p)\cdot 0^{ k} + p\cdot 1^{k}= p.$$ | ||
| + | |||
| + | *From this follows with $p = 1/4$ and $k=2$: | ||
| + | :$$m_{b}= m_{2b}= p, \hspace{0.5cm} \sigma_{\it b}=\sqrt{p\cdot (1- p)}\hspace{0.15cm} \underline{=\rm 0.433} .$$ | ||
| + | |||
| + | |||
| + | '''(3)''' For the random variable $c$ holds: | ||
| + | :$$m_{\it c} = 0\hspace{0.3cm} ({\rm symmetric\hspace{0.1cm}um\hspace{0.1cm}0)},$$ | ||
| + | :$$ m_{2\it c}= {1}/{4}\cdot(-1)^2+{1}/{2}\cdot 0^2+{1}/{4}\cdot (1)^2={1}/{2} \hspace{0.5cm}$$ | ||
| + | :$$\Rightarrow \hspace{0.5cm}\sigma_{\it c}=\rm \sqrt{1/2}\hspace{0.15cm} \underline{=0.707}.$$ | ||
| + | |||
| − | + | '''(4)''' According to the general rules for expected values, with $p = 0.25$: | |
| − | :$$ \it | + | :$$m_{\it d} = {\rm E}\big[a-2 b+c\big]= {\rm E}\big[a\big] \hspace{0.1cm} -\hspace{0.1cm}\rm 2 \hspace{0.05cm}\cdot\hspace{0.05cm} {\rm E}\big[ b\big]\hspace{0.1cm}+\hspace{0.1cm} {\rm E}\big[ c\big] = m_{ a}\hspace{0.1cm}-\hspace{0.1cm}2\hspace{0.05cm}\cdot\hspace{0.05cm} m_{\it b}\hspace{0.1cm}+\hspace{0.1cm} m_{\it c} = 0-2\hspace{0.05cm}\cdot\hspace{0.05cm} p + 0 \hspace{0.15cm} \underline{= -0.5}.$$ |
| − | |||
| − | |||
| − | + | '''(5)''' Analogous to the subtask '''(4)''' we obtain for the second order moment: | |
| − | :$$\rm \ | + | :$$m_{2d}= {\rm E}\big[( a-2b+c)^{\rm 2}\big] = {\rm E}\big[a^{\rm 2}\big]\hspace{0.1cm}+\hspace{0.1cm}4\hspace{0.05cm}\cdot\hspace{0.05cm} {\rm E}\big[ b^{\rm 2}\big]\hspace{0.1cm}+\hspace{0.1cm} {\rm E}\big[c^{\rm 2}\big]\hspace{0.1cm} - \hspace{0.1cm}4\hspace{0.05cm}\cdot\hspace{0.05cm} {\rm E}\big[a\hspace{0.05cm}\cdot \hspace{0.05cm}b\big]\hspace{0.1cm}+\hspace{0.1cm} 2\hspace{0.05cm}\cdot\hspace{0.05cm}{\rm E}\big[ a\hspace{0.05cm}\cdot \hspace{0.05cm}c\big]\hspace{0.1cm}-\hspace{0.1cm} 4\hspace{0.05cm}\cdot\hspace{0.05cm}{\rm E}\big[ b\hspace{0.05cm}\cdot \hspace{0.05cm}c\big].$$ |
| − | |||
| − | + | *But since $a$ and $b$ are statistically independent of each other, also holds: | |
| − | :$$ | + | :$${\rm E}\big[a\cdot b\big] = {\rm E}\big[ a\big] \cdot {\rm E}\big[ b\big]= m_{ a}\cdot m_{ b} = 0, \hspace{0.2cm} {\rm da}\hspace{0.2cm} m_{ a}=\rm 0.$$ |
| − | + | *The same holds for the other mixed terms. Therefore, using $p = 0.25$, we obtain: | |
| − | :$$m_{ | + | :$$ m_{2 d}=m_{2 a}+4\cdot m_{ 2 b}+m_{ 2 c}=1+4\cdot p+0.5\hspace{0.15cm} \underline{=\rm 2.5}.$$ |
| − | |||
| − | |||
| − | + | '''(6)''' For general $p$ resp. for $p = 0.25$ results: | |
| − | :$$ \ | + | :$$\sigma_{\it d}^{\rm 2}=1.5+4\cdot p - 4 \cdot p^{\rm 2}=2.25 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} \sigma_{d}\hspace{0.15cm} \underline{=\rm 1.5}.$$ |
| − | + | *The maximum variance for $p = 0.50$ results in $\sigma_{\it d}^{\rm 2}=2.50$. | |
| − | |||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Theory of Stochastic Signals: Exercises|^2.2 Moments of Discrete Random Variables^]] |
Latest revision as of 13:20, 18 January 2023
Let be given three discrete random variables $a$, $b$ and $c$, which are defined as the instantaneous values of the represented signals. These have the following properties:
- The random variable $a$ can take the two values $+1$ and $-1$ with equal probability.
- The random variable $b$ is also two-point distributed, but with ${\rm Pr}(b = 1) = p$ and ${\rm Pr}(b = 0) = 1 - p$.
- The probabilities of the random variable $c$ be ${\rm Pr}(c = 0) = 1/2$ and ${\rm Pr}(c = +1) = Pr(c = -1) =1/4$.
- There are no statistical dependencies between the three random variables $a$, $b$ and $c$.
- Another random variable $d$ is formed from the random variables $a$, $b$ and $c$:
- $$d=a-2 b+c.$$
The graph shows sections of these random variables. It can be seen that $d$ can take all integer values between $-4$ and $+2$ .
Hints:
- The exercise belongs to the chapter Moments of a Discrete Random Variable.
- The topic of this chapter is illustrated with examples in the (German language) learning video
"Momentenberechnung bei diskreten Zufallsgrößen" ⇒ "Calculating Moments for Discrete-Valued Random Variables"
Questions
Solution
(1) Due to the symmetry holds:
- $$\rm \it m_{\it a}=\rm 0; \hspace{0.5cm}\it m_{\rm 2\it a}=\rm 0.5\cdot (-1)^2 + 0.5\cdot (1)^2{ = 1}.$$
- From this one obtains with Steiner's theorem:
- $$\it\sigma_a^{\rm 2} = \rm\sqrt{1-0^2}=1 \hspace{0.5cm}or \hspace{0.5cm}\it\sigma_a\hspace{0.15cm} \underline{=\rm 1}.$$
(2) In general, for the $k$–th order moment:
- $$ m_{k}=(1-p)\cdot 0^{ k} + p\cdot 1^{k}= p.$$
- From this follows with $p = 1/4$ and $k=2$:
- $$m_{b}= m_{2b}= p, \hspace{0.5cm} \sigma_{\it b}=\sqrt{p\cdot (1- p)}\hspace{0.15cm} \underline{=\rm 0.433} .$$
(3) For the random variable $c$ holds:
- $$m_{\it c} = 0\hspace{0.3cm} ({\rm symmetric\hspace{0.1cm}um\hspace{0.1cm}0)},$$
- $$ m_{2\it c}= {1}/{4}\cdot(-1)^2+{1}/{2}\cdot 0^2+{1}/{4}\cdot (1)^2={1}/{2} \hspace{0.5cm}$$
- $$\Rightarrow \hspace{0.5cm}\sigma_{\it c}=\rm \sqrt{1/2}\hspace{0.15cm} \underline{=0.707}.$$
(4) According to the general rules for expected values, with $p = 0.25$:
- $$m_{\it d} = {\rm E}\big[a-2 b+c\big]= {\rm E}\big[a\big] \hspace{0.1cm} -\hspace{0.1cm}\rm 2 \hspace{0.05cm}\cdot\hspace{0.05cm} {\rm E}\big[ b\big]\hspace{0.1cm}+\hspace{0.1cm} {\rm E}\big[ c\big] = m_{ a}\hspace{0.1cm}-\hspace{0.1cm}2\hspace{0.05cm}\cdot\hspace{0.05cm} m_{\it b}\hspace{0.1cm}+\hspace{0.1cm} m_{\it c} = 0-2\hspace{0.05cm}\cdot\hspace{0.05cm} p + 0 \hspace{0.15cm} \underline{= -0.5}.$$
(5) Analogous to the subtask (4) we obtain for the second order moment:
- $$m_{2d}= {\rm E}\big[( a-2b+c)^{\rm 2}\big] = {\rm E}\big[a^{\rm 2}\big]\hspace{0.1cm}+\hspace{0.1cm}4\hspace{0.05cm}\cdot\hspace{0.05cm} {\rm E}\big[ b^{\rm 2}\big]\hspace{0.1cm}+\hspace{0.1cm} {\rm E}\big[c^{\rm 2}\big]\hspace{0.1cm} - \hspace{0.1cm}4\hspace{0.05cm}\cdot\hspace{0.05cm} {\rm E}\big[a\hspace{0.05cm}\cdot \hspace{0.05cm}b\big]\hspace{0.1cm}+\hspace{0.1cm} 2\hspace{0.05cm}\cdot\hspace{0.05cm}{\rm E}\big[ a\hspace{0.05cm}\cdot \hspace{0.05cm}c\big]\hspace{0.1cm}-\hspace{0.1cm} 4\hspace{0.05cm}\cdot\hspace{0.05cm}{\rm E}\big[ b\hspace{0.05cm}\cdot \hspace{0.05cm}c\big].$$
- But since $a$ and $b$ are statistically independent of each other, also holds:
- $${\rm E}\big[a\cdot b\big] = {\rm E}\big[ a\big] \cdot {\rm E}\big[ b\big]= m_{ a}\cdot m_{ b} = 0, \hspace{0.2cm} {\rm da}\hspace{0.2cm} m_{ a}=\rm 0.$$
- The same holds for the other mixed terms. Therefore, using $p = 0.25$, we obtain:
- $$ m_{2 d}=m_{2 a}+4\cdot m_{ 2 b}+m_{ 2 c}=1+4\cdot p+0.5\hspace{0.15cm} \underline{=\rm 2.5}.$$
(6) For general $p$ resp. for $p = 0.25$ results:
- $$\sigma_{\it d}^{\rm 2}=1.5+4\cdot p - 4 \cdot p^{\rm 2}=2.25 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} \sigma_{d}\hspace{0.15cm} \underline{=\rm 1.5}.$$
- The maximum variance for $p = 0.50$ results in $\sigma_{\it d}^{\rm 2}=2.50$.