Difference between revisions of "Signal Representation/The Fourier Transform Theorems"
| (92 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Aperiodic Signals - Impulses |
| − | |Vorherige Seite= | + | |Vorherige Seite=Special Cases of Impulse Signals |
| − | |Nächste Seite= | + | |Nächste Seite=The Convolution Theorem and Operation |
}} | }} | ||
| − | == | + | ==Multiplication with a factor - Addition Theorem== |
| − | + | <br> | |
| − | In | + | In this section the »'''Fourier Transform Theorems'''« are assembled. These can be used, for examle, to derive from already known transformations |
| − | $$x( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X( f ),\quad x_1 ( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X_1 ( f ),\quad x_2 ( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X_2 ( f )$$ | + | :$$x( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X( f ),\quad x_1 ( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X_1 ( f ),\quad x_2 ( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X_2 ( f )$$ |
| − | + | new functional relationships. Here we restrict ourselves to real time functions. | |
| − | {{ | + | {{BlaueBox|TEXT= |
| − | + | $\text{Theorem:}$ A $\text{constant factor}$ $k$ affects the time and spectral function in the same way: | |
| − | $$k \cdot x(t)\;\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,k \cdot X(f).$$ | + | :$$k \cdot x(t)\ \;\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\ k \cdot X(f).$$}} |
| − | |||
| − | + | :This relation can be used for simplification by omitting the constant $k$ $($which can be a gain, an attenuation or a unit factor$)$ and adding it to the result later. | |
| − | + | :The above sentence follows directly from the definition of the [[Signal_Representation/The_Fourier_Transform_and_its_Inverse#The_first_Fourier_integral|»first Fourier integral«]], as well as from the »addition theorem«, which formulates the foundation of the »superposition principle«. | |
| − | {{ | + | {{BlaueBox|TEXT= |
| − | + | $\text{Addition Theorem:}$ If a time function can be written as a sum of single functions, the resulting spectral function is the sum of the resulting single spectra: | |
| − | $$x( t ) = x_1 ( t ) + x_2 ( t )\quad\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\quad X( f ) = X_1 (f) + X_2 ( f ).$$ | + | :$$x( t ) = x_1 ( t ) + x_2 ( t )\quad\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\quad X( f ) = X_1 (f) + X_2 ( f ).$$ }} |
| − | |||
| + | {{GraueBox|TEXT= | ||
| + | [[File:P_ID2722__Sig_T_3_3_S1.png|right|frame|Rectangular pulse, triangular pulse and their combination]] | ||
| + | $\text{Example 1:}$ The following Fourier correspondences are known: | ||
| − | {{ | + | *The rectangular pulse: |
| + | :$$x_1 ( t )\hspace{0.15cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X_1 ( f )=T \cdot {\rm sinc}(f T),$$ | ||
| + | *the triangle pulse: | ||
| + | :$$ x_2 ( t )\hspace{0.15cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X_2 ( f )=T /2\cdot {\rm sinc}^2(f T/2).$$ | ||
| − | + | These two pulses are sketched on the right as red and blue curve respectively. | |
| − | + | ||
| + | ⇒ Then for the Fourier correspondences of the green drawn $($weighted$)$ sum signal $x(t)$ holds: | ||
| + | |||
| + | :$$x(t) = {1}/{3} \cdot x_1 ( t ) + {2}/{3} \cdot x_2 ( t )\hspace{0.15cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X(f) = {1}/{3} \cdot X_1 ( f ) + {2}/{3} \cdot X_2 ( f ).$$}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | All theorems presented in this chapter can be found at the following $($German language$)$ learning video with illustrated examples<br> [[Gesetzmäßigkeiten_der_Fouriertransformation_(Lernvideo)|»Gesetzmäßigkeiten der Fouriertransformation«]] ⇒ "Regularities to the Fourier transform". | |
| − | |||
| − | |||
| − | |||
| + | ==Assignment Theorem== | ||
| + | <br> | ||
| + | With the [[Signal_Representation/Fourier_Series#Complex_Fourier_series|»complex Fourier series«]] for describing periodic signals, we have found | ||
| + | #that an even function always leads to real Fourier coefficients, and | ||
| + | #an odd function exclusively to imaginary Fourier coefficients. | ||
| − | |||
| − | + | The Fourier transform shows similar properties. | |
| − | {{ | + | {{BlaueBox|TEXT= |
| − | + | $\text{Assignment Theorem:}$ If a real time function consists additively of an even $($German: "gerade" ⇒ $\text{"g"})$ and an odd $($German: "ungerade" ⇒ $\text{"u"})$ part, | |
| − | $$x( t ) = x_{\rm g} ( t ) + x_{\rm u} ( t ),$$ | + | :$$x( t ) = x_{\rm g} ( t ) + x_{\rm u} ( t ),$$ |
| − | + | then the following applies for its spectral function: | |
| − | + | :$$X(f) = X_{\rm R}(f) + {\rm j}\cdot X_{\rm I}(f), \hspace{0.5cm}\text{with}$$ | |
| − | $$X(f) = X_{\rm R}(f) + {\rm j}\cdot X_{\rm I}(f), \hspace{0.5cm}\text{ | + | ::$$ x_{\rm g} (t) \hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X_{\rm R}(f),$$ |
| + | ::$$x_{\rm u} (t) \hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} {\rm j} \cdot X_{\rm I} (f).$$ | ||
| − | + | The real part $X_{\rm R}(f)$ of the spectrum is then also even, while $X_{\rm I}(f)$ describes an odd function of frequency.}} | |
| − | |||
| + | *The assignment theorem can be easily proved by considering the theorem of [https://en.wikipedia.org/wiki/Leonhard_Euler »$\text{Leonhard Euler}$«]: | ||
| + | :$${\rm e}^{ - {\rm j}\omega _0 t} = \cos ( {\omega _0 t} ) - {\rm j}\cdot \sin ( {\omega _0 t} ).$$ | ||
| − | + | *The even and odd part of each function $x(t)$ can be calculated with the following equations: | |
| − | $$x_{\rm g} (t) = {1}/{2}\ | + | :$$x_{\rm g} (t) = {1}/{2}\big[ {x(t) + x(-t)} \big],$$ |
| + | :$$x_{\rm u} (t) = {1}/{2}\big[ {x(t) - x(-t)} \big].$$ | ||
| − | {{ | + | {{GraueBox|TEXT= |
| + | [[File:P_ID472__Sig_T_3_3_S2.png|right|frame|Spectrum of the jump function]] | ||
| + | $\text{Example 2:}$ | ||
| + | We consider the »jump function« | ||
| + | :$$x(t) = \gamma (t) = \bigg\{ \begin{array}{l} 0\quad \quad {\rm for}\;t < 0 \\ 1\quad \quad{\rm for}\; t > 0 \\ \end{array} ,$$ | ||
| − | + | which can be split as follows: | |
| − | |||
| − | |||
| − | |||
| − | + | :$$\gamma (t) = {1}/{2} +{1}/{2} \cdot {\rm sign}(t).$$ | |
| − | + | The »signum function« was used here: | |
| − | $${\rm sign} (t) = \bigg\{ \begin{array}{l} -1\quad \quad {\rm | + | :$${\rm sign} (t) = \bigg\{ \begin{array}{l} -1\quad \quad {\rm for}\;t < 0, \\ +1\quad \quad{\rm for}\; t > 0. \\ \end{array} $$ |
| − | + | Therefore the following applies: | |
| − | + | #The even $($blue$)$ signal part $x_{\rm g} (t) = {1}/{2}$ is a constant with the real spectral function $X_{\rm R}(f) = {1}/{2} \cdot \delta(f)$. | |
| − | + | #The spectrum ${\rm j} \cdot X_{\rm I}(f)$ of the odd $($green$)$ signum function $x_{\rm u} (t)$ was already calculated in the earlier [[Signal_Representation/Fourier_Transform_and_Its_Inverse#Fourier_transform|$\text{Example 3}$]] in the section »Fourier transform«. | |
| − | + | #This results for the spectrum of the $($red$)$ sketched jump function: | |
| − | + | ::$$X(f) = X_{\rm R}(f) + {\rm j}\cdot X_{\rm I}(f)= {1}/{2} \cdot \delta (f) - {\rm j}\cdot \frac{1}{2\pi f}.$$}} | |
| − | $$X(f) = X_{\rm R}(f) + {\rm j}\cdot X_{\rm I}(f)= {1}/{2} \cdot \delta (f) - {\rm j}\cdot \frac{1}{2\pi f}.$$ | ||
| − | |||
| + | ==Similarity Theorem== | ||
| + | <br> | ||
| + | The similarity theorem shows the relation between the spectral functions of two time signals of the same shape, stretched or compressed. | ||
| − | = | + | {{BlaueBox|TEXT= |
| + | $\text{Similarity Theorem:}$ If $X(f)$ is the Fourier transform of $x(t)$, then with the real constant $k$ the following relation applies: | ||
| + | |||
| + | :$$x( {k \cdot t} )\hspace{0.15cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} \frac{1}{\left \vert \hspace{0.05cm} k\hspace{0.05cm} \right \vert} \cdot X( {f}/{k} ).$$}} | ||
| − | |||
| − | {{ | + | {{BlaueBox|TEXT= |
| − | + | $\text{Proof:}$ For positive $k$ follows from the Fourier integral with the substitution $\tau = k \cdot t$: | |
| − | $$x( {k \cdot t} )\hspace{0.1cm} \ | + | :$$\int_{ - \infty }^{ + \infty } {x( {k \cdot t})} \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}ft} \hspace{0.1cm}{\rm d}t = \frac{1}{k} \cdot \int_{ - \infty }^{ + \infty } {x( \tau )} \cdot {\rm e}^{ - {\rm j}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm} f/k \hspace{0.05cm}\cdot \hspace{0.05cm}\tau } \hspace{0.1cm}{\rm d} \tau = \frac{1}{k}\cdot X( {{f}/{k}}).$$ |
| − | + | *For negative $k$ the integration limits would be mixed up and you get $-1/k \cdot X(f/k)$. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | $ | + | *Since in the equation $\vert \hspace{0.05cm} k \hspace{0.05cm} \vert$ is used, the result is valid for both signs. |
| − | + | <div align="right">q.e.d.</div>}} | |
| − | |||
| − | <div align="right">q.e.d.</div> | ||
| − | |||
| + | The effects of the similarity theorem can be illustrated, for example, with an audio tape. | ||
| + | *If such a tape is played with double speed, this corresponds to a compression of the time signal $(k = 2)$. | ||
| − | + | *Thus the frequencies appear twice as high. | |
| − | {{ | + | {{GraueBox|TEXT= |
| + | [[File:P_ID473__Sig_T_3_3_S3_neu.png|right|frame|Two rectangles of different width]] | ||
| + | $\text{Example 3:}$ | ||
| + | We consider two rectangles of equal height, where $T_2 = T_1/2$ holds. | ||
| − | + | *The spectral function of $x_1(t)$ results after the [[Signal_Representation/The_Fourier_Transform_and_its_Inverse#The_first_Fourier_integral|»first Fourier Integral«]] to | |
| − | |||
| − | |||
| − | $$X_1 (f) = A \cdot \frac{{1 - {\rm e}^{ - {\rm j}2\pi fT_1 } }}{{{\rm j}2\pi f}} .$$ | + | :$$X_1 (f) = A \cdot \frac{ {1 - {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 } } }{ { {\rm j}2\pi f} } .$$ |
| − | + | *For this can also be written: | |
| − | |||
| − | |||
| − | + | :$$X_1 (f) = A \cdot T_1 \cdot \frac{{{\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 } - {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 } }}{{{\rm j}2\pi fT_1 }} \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 } = A \cdot T_1 \cdot {\rm sinc}( {f T_1 } ) \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 }.$$ | |
| − | |||
| − | $$ | ||
| − | + | *For the spectral function of $x_2(t)$ follows from the similarity theorem with $k = -2$: | |
| − | $$X_2 (f) = A \cdot | + | :$$X_2 (f) = \frac{1}{2} \cdot X_1 ( { - {f}/{2}} ) = \frac{A \cdot T_1 }{2} \cdot {\rm sinc}( { - f {T_1 }/{2} } ) \cdot {\rm e}^{ {\rm j}\pi fT_1 /2} .$$ |
| − | {{ | + | * The function $\text{sinc}(x) = \sin(x)/x$ is even: $\text{sinc}(-x) = \text{sinc}(x)$. Therefore you can omit the sign in the argument of the $\text{sinc}$–function. |
| + | *With $T_2 = T_1/2$ one gets: | ||
| + | |||
| + | :$$X_2 (f) = A \cdot T_2 \cdot {\rm sinc}( {fT_2 } ) \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}T_2 } .$$}} | ||
| − | |||
| − | + | ==Reciprocity Theorem of time duration and bandwidth== | |
| − | + | <br> | |
| + | This law follows directly from the [[Signal_Representation/Fourier_Transform_Theorems#Similarity_Theorem|»similarity theorem«]]: The wider a pulse is in its extension, the narrower and higher is the corresponding spectrum and vice versa. | ||
| − | + | :To be able to make quantitative statements, we define two parameters for energy-limited signals. Both quantities are shown in the diagram in $\text{Example 4}$ for a Gaussian pulse and its likewise Gaussian spectrum. | |
| − | |||
| − | |||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Definition:}$ | ||
| + | The »'''equivalent pulse duration'''« is derived from the time course. It is equal to the width of an area–equal rectangle with same height as $x(t)$: | ||
| − | :$$\Delta | + | :$$\Delta t = \frac{1}{{x( {t = 0} )}} \cdot \int_{ - \infty }^{ + \infty } {x( t)} \hspace{0.1cm}{\rm d}t.$$}} |
| − | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Definition:}$ | ||
| + | The »'''equivalent bandwidth'''« is defined in the frequency domain. It gives the width of the area–equal rectangle with same height as spectrum $X(f)$: | ||
| + | |||
| + | :$$\Delta f = \frac{1}{{X( {f = 0} )}}\cdot \int_{ - \infty }^{ + \infty } {X( f )} \hspace{0.1cm} {\rm d}f.$$}} | ||
| − | {{ | + | {{BlaueBox|TEXT= |
| − | + | $\text{Reciprocity Theorem:}$ The product of the equivalent pulse duration and the equivalent bandwidth is always the same $1$: | |
| − | $$\Delta t \cdot \Delta f = 1$$ | + | :$$\Delta t \cdot \Delta f = 1.$$}} |
| − | |||
| − | {{ | + | {{BlaueBox|TEXT= |
| − | + | $\text{Proof:}$ | |
| − | + | Based on the two Fourier integrals, for $f = 0$ resp. $t = 0$: | |
| − | |||
| − | |||
| − | $$X( {f = 0} ) = \int_{ - \infty }^{ + \infty } {x(t)\hspace{0.1cm}{\rm d}t,} | + | :$$X( {f = 0} ) = \int_{ - \infty }^{ + \infty } {x(t)\hspace{0.1cm}{\rm d}t,}$$ |
| + | :$$x( {t = 0} ) = \int_{ - \infty }^{ + \infty } {X(f)\hspace{0.1cm}{\rm d}f.}$$ | ||
| − | + | If you take this result into account in the above definitions, you get | |
| − | $$\Delta t = \frac{{X( {f = 0} )}}{{x( {t = 0} )}}, \hspace{0.5cm}\Delta f = \frac{{x( {t = 0} )}}{{X( {f = 0} )}}.$$ | + | :$$\Delta t = \frac{{X( {f = 0} )}}{{x( {t = 0} )}}, \hspace{0.5cm}\Delta f = \frac{{x( {t = 0} )}}{{X( {f = 0} )}}.$$ |
| − | + | From this $\Delta t \cdot \Delta f = 1$ follows directly. <div align="right">q.e.d.</div>}} | |
| − | |||
| + | Note that $\Delta f$ is defined over the actual spectrum $X(f)$ and not over $|X(f)|$. | ||
| + | *For real functions the integration over the even function part is sufficient, since the integral over the odd part is always zero due to the [[Signal_Representation/Fourier_Transform_Theorems#Assignment_Theorem|»assignment theorem«]]. | ||
| − | + | *For odd time functions and thus purely imaginary spectra, the two definitions of $\Delta t$ and $\Delta f$ fail. | |
| − | * | ||
| − | |||
| − | {{ | + | {{GraueBox|TEXT= |
| − | + | $\text{Example 4:}$ | |
| − | + | The graph illustrates the equivalent pulse duration $\Delta t$ and the equivalent bandwidth $\Delta f$ exemplary for the Gaussian pulse. | |
| − | + | [[File:Sig_T_3_4_S4_version2.png|right|frame|Gaussian example for the reciprocity theorem]] | |
| − | |||
| + | Furthermore, it is valid: | ||
| + | *Widening the Gaussian pulse by the factor $3$ will reduce the equivalent bandwidth by the same factor. | ||
| − | + | ||
| + | *If the pulse amplitude $x(t = 0)$ is not changed, the integral area above $X(f)$ remains constant. | ||
| − | = | + | *This means that $X(f=0)$ is simultaneously increased by the factor $3$ .}} |
| − | + | ==Duality Theorem== | |
| + | <br> | ||
| + | This regularity is particularly useful for obtaining new Fourier correspondences. | ||
| − | {{ | + | {{BlaueBox|TEXT= |
| − | + | $\text{Duality Theorem:}$ If $X(f)$ is the Fourier transform of $x(t)$, then: | |
| − | $$X^{\star}(t)\hspace{0. | + | :$$X^{\star}(t)\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}x^{\star}( f ).$$ |
| − | + | If we restrict ourselves to real time functions, the signs for »conjugated complex» can be omitted on both sides of the Fourier correspondence.}} | |
| − | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Proof:}$ The [[Signal_Representation/The_Fourier_Transform_and_its_Inverse#The_first_Fourier_integral|»first Fourier integral«]] is after successive renaming $t \to u$, $f \to t$: | ||
| + | |||
| + | :$$X( f ) = \int_{ - \infty }^{ + \infty } {x( u )} \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}u} \hspace{0.1cm}{\rm d}u, \hspace{1cm} | ||
| + | X(t ) = \int_{ - \infty }^{ + \infty } {x( u )} \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}t\hspace{0.05cm}\cdot \hspace{0.05cm}u}\hspace{0.1cm} {\rm d}u.$$ | ||
| − | + | *If you change the sign in the exponent, you have to replace $X(t)$ by $X^*(t)$ and $x(u)$ by $x^*(u)$ : | |
| − | |||
| − | $$X( | + | :$$X^{\star}(t ) = \int_{ - \infty }^{ + \infty } {x^{\star}( u )} \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi\hspace{0.05cm}\cdot \hspace{0.05cm} t\hspace{0.05cm}\cdot \hspace{0.05cm}u}\hspace{0.1cm} {\rm d}u.$$ |
| − | |||
| − | + | *With the further renaming $u \to f$ one gets to the [[Signal_Representation/The_Fourier_Transform_and_its_Inverse#The_second_Fourier_integral|»second Fourier integral«]]: | |
| − | $$X^{\star}(t ) = \int_{ - \infty }^{ + \infty } {x^{\star}( | + | :$$X^{\star}(t ) = \int_{ - \infty }^{ + \infty } {x^{\star}( f )} \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}f.\hspace{7.9cm}$$ |
| − | + | <div align="right">q.e.d.</div>}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | {{ | + | {{GraueBox|TEXT= |
| − | [[File:P_ID475__Sig_T_3_3_S5_neu.png|right| | + | [[File:P_ID475__Sig_T_3_3_S5_neu.png|right|frame|$\text{Above: Rectangular-in-time}$ ⇒ $\text{sinc-in-frequency};$ <br>$\text{below; sinc-in-time}$ ⇒ $\text{rectangular-in-frequency}$]] |
| − | + | $\text{Example 5:}$ | |
| − | |||
| − | $ | ||
| − | + | The figure on the right shows an application of the duality theorem, namely the functional relations between | |
| − | * | + | * a signal $x_1(t)$ with rectangular time function, and |
| − | |||
| + | * a signal $x_2(t)$ with rectangular spectral function. | ||
| − | |||
| − | |||
| − | + | $\text{Another Example:}$ | |
| − | + | *The spectrum $X(f) = \delta(f)$ of the DC signal $x(t) = 1$ is assumed to be known. | |
| − | |||
| − | |||
| − | |||
| − | + | *According to the »duality theorem«, the spectral function of the Dirac delta is therefore: | |
| − | + | :$$ x(t) = \delta(t)\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X(f)= 1.$$ | |
| − | |||
| − | + | }} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==Shifting Theorem== | |
| + | <br> | ||
| + | We now consider | ||
| + | *a shift of the time function, e.g. caused by a delay; | ||
| + | * or a frequency shift, as it occurs for example with [[Modulation_Methods/Double-Sideband_Amplitude_Modulation#Description_in_the_frequency_domain|»analog double-sideband amplitude modulation«]]. | ||
| − | |||
| − | + | {{BlaueBox|TEXT= | |
| − | + | $\text{Shifting Theorem:}$ If $X(f)$ is the Fourier transform of $x(t)$, the following correspondences also apply: | |
| − | $$ | + | $$\mathbf{(1)}\hspace{0.5cm}x( {t - t_0 } )\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X( f ) \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm} f\hspace{0.05cm}\cdot \hspace{0.05cm}t_0 },$$ |
| − | + | $$\mathbf{(2)}\hspace{0.5cm}x( t ) \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_0 \hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X( {f - f_0 } ).$$ | |
| − | $$ | + | Here, $t_0$ and $f_0$ are any time or frequency values.}} |
| − | |||
| − | |||
| − | |||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Proof of Equation (1):}$ | ||
| + | The [[Signal_Representation/The_Fourier_Transform_and_its_Inverse#The_first_Fourier_integral|»first Fourier integral«]] for signal $x_{\rm V}(t) = x(t-t_0)$ shifted to the right by $t_0$ is defined with the substitution $\tau = t - t_0$: | ||
| − | {{ | + | :$$X_{\rm V} ( f ) = \int_{ - \infty }^{ + \infty } {x( {t - t_0 } ) \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm}{\rm d}t} |
| + | = \int_{ - \infty }^{ + \infty } {x( \tau ) \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}( {\tau + t_0 } )}\hspace{0.1cm} {\rm d}\tau .}$$ | ||
| + | *The term independent from the integration variable $\tau$ can be dragged in front of the integral. | ||
| − | == | + | *With the renaming $\tau \to t$ one then obtains |
| + | |||
| + | :$$X_{\rm V}( f ) = {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}t_0 } \cdot \int_{ - \infty }^{ + \infty } {x( t )} \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}t = {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}t_0 } \cdot X( f).$$ | ||
| + | <div align="right">q.e.d.</div>}} | ||
| − | |||
| − | {{ | + | {{GraueBox|TEXT= |
| − | + | [[File:P_ID478__Sig_T_3_3_S6_neu.png|right|frame|Shifting theorem example]] | |
| + | $\text{Example 6:}$ As already mentioned, the symmetrical rectangular pulse $x_1(t)$ has the spectrum | ||
| − | $$\ | + | :$$X_1 ( f ) = A \cdot T \cdot {\rm si}( {\pi fT} )= A \cdot T \cdot {\rm sinc}( {fT} )$$ |
| + | :$$\hspace{0.9cm} \text{with} \hspace{0.5cm} {\rm si}(x)= \sin(x)/x,\hspace{0.5cm}{\rm sinc}(x)= \sin(\pi x)/(\pi x)={\rm si}(x/\pi).$$ | ||
| − | $$ | + | *The rectangular pulse $x_2(t)$ displayed below is shifted to the right with respect to $x_1(t)$ by $T/2$: |
| + | :$$x_2(t) = x_1(t-T/2).$$ | ||
| + | *Thus its spectrum is: | ||
| + | |||
| + | :$$X_2( f ) = A \cdot T \cdot {\rm sinc}( {fT} ) \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}T} .$$ | ||
| − | + | *This spectral function can also be written as follows with the [[Signal_Representation/Calculating_with_Complex_Numbers#Representation_by_magnitude_and_phase|»theorem of Euler«]] and some trigonometric conversions: | |
| − | {{ | + | |
| + | :$$X_2( f ) = \frac{A }{2\pi f} \cdot \sin ( 2\pi fT) + {\rm j}\cdot \frac{A }{2\pi f} \cdot \big[ {\cos ( {2\pi fT} ) - 1} \big] .$$ | ||
| + | *The same result can be obtained with the [[Signal_Representation/Fourier_Transform_Theorems#Assignment_Theorem|»assignment theorem«]]; <br>⇒ The real part of the spectrum belongs to the even signal part $x_{\rm g}(t)$, the imaginary part to the odd signal part $x_{\rm u}(t)$.}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==Differentiation Theorem== | |
| − | + | <br> | |
| − | $ | + | This theorem shows, how the differentiation of a function $x(t)$ resp. $X(f)$ affects the corresponding Fourier transform; it is also applicable several times. |
| − | + | A simple example for the application of this theorem is the relation between current $i(t)$ and voltage $u(t)$ of a capacitance $C$ according to the equation | |
| + | :$$i(t) = C \cdot \text{d}u(t)/\text{d}t.$$ | ||
| − | {{ | + | {{BlaueBox|TEXT= |
| + | $\text{Differentiation Theorem:}$ If $X(f)$ is the Fourier transform of $x(t)$, the following two correspondences are also valid: | ||
| + | $$\mathbf{(1)}\hspace{0.5cm}\frac{{{\rm d}x( t )}}{{{\rm d}t}}\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi f \cdot X( f ),$$ | ||
| + | |||
| + | $$\mathbf{(2)}\hspace{0.5cm}- t \cdot x( t )\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}\frac{1}{{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi }} \cdot \frac{{{\rm d}X( f )}}{{{\rm d}f}}.$$}} | ||
| − | |||
| − | + | {{BlaueBox|TEXT= | |
| − | + | $\text{Proof of Equation (1):}$ This equation results from differentiation of the [[Signal_Representation/The_Fourier_Transform_and_its_Inverse#The_second_Fourier_integral|»second Fourier integral«]]: | |
| − | $$\ | + | :$$y(t) = \frac{\text{d}x(t)}{\text{d}t} = \frac{\text{d} }{\text{d}t}\int_{ - \infty }^{ + \infty } X( f ) \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\hspace{0.03cm}\pi\hspace{0.05cm}\cdot \hspace{0.05cm} f\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}f = \int_{ - \infty }^{ + \infty } {X( f )} \cdot {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi f \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm} f\hspace{0.05cm}\cdot \hspace{0.05cm}t} {\rm d}f.$$ |
| − | |||
| − | + | At the same time is: | |
| − | + | ||
| − | + | :$$y( t ) = \int_{ - \infty }^{ + \infty } {Y( f )} \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\hspace{0.03cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}f.$$ | |
| + | #By comparing the integrands, the variation $\mathbf{(1)}$ of the differentiation theorem is obtained. | ||
| + | #To derive the second variant one proceeds from the [[Signal_Representation/The_Fourier_Transform_and_its_Inverse#The_first_Fourier_integral|»first Fourier integral«]] in an analogous manner. | ||
| + | #The negative exponent in the first Fourier integral leads to the minus sign in the time function. <div align="right">q.e.d.</div>}} | ||
| + | |||
| − | {{ | + | {{GraueBox|TEXT= |
| − | + | [[File:P_ID484__Sig_T_3_3_S7_neu.png|right|frame|Correlation between »jump« and »Dirac delta«]] | |
| + | $\text{Example 7:}$ | ||
| + | The spectra of the signals $x_1(t)$ and $x_2(t)$ were already calculated in the previous examples: | ||
| + | |||
| + | :$$X_1( f ) = \frac{1 }{ {\rm j\cdot \pi} f}, $$ | ||
| + | :$$X_2( f ) = 2 = {\rm const.}\hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm} X_2(f) = X_1(f) \cdot {\rm j}\cdot 2\pi f.$$ | ||
| + | #From the differentiation theorem it follows that $x_2(t)$ is equal to the time-derivative of $x_1(t)$ . | ||
| + | #This is actually correct: For $t \neq 0$ ⇒ $x_1(t)$ is constant, i.e. the derivative is zero. | ||
| + | #For $t=0$ the gradient is infinitely large, which is also expressed in the equation $x_2(t) = 2 \cdot \delta(t)$. | ||
| + | #The impulse weight "$2$" of $x_2(t)$ considers that the jump within $x_1(t)$ at $t = 0$ has the height "$2$". }} | ||
| − | |||
| − | + | ==Integration Theorem== | |
| + | <br> | ||
| + | Integration is just like differentiation a linear operation. This results in the following theorem: | ||
| − | {{ | + | {{BlaueBox|TEXT= |
| − | + | $\text{Integration Theorem:}$ If $X(f)$ is the Fourier transform $($spectral function$)$ of $x(t)$, then the following Fourier correspondences also apply: | |
| − | $$\int_{ - \infty }^{\hspace{0.05cm}t} {x( \tau )} \hspace{0.1cm}{\rm d}\tau\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X( f )\left( {\frac{1}{{{\rm j}2\pi f}} + \frac{1}{2}\cdot \delta ( f )} \right),$$ | + | $$\mathbf{(1)}\hspace{0.5cm}\int_{ - \infty }^{\hspace{0.05cm}t} {x( \tau )} \hspace{0.1cm}{\rm d}\tau \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ \ X( f )\left( {\frac{1}{{{\rm j}\cdot 2\pi f}} + \frac{1}{2}\cdot \delta ( f )} \right),$$ |
| − | $$x( t )\left( { - \frac{1}{{{\rm j}2\pi t}} + \frac{1}{2}\cdot \delta ( t )} \right)\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\int_{ - \infty }^f {X( \nu ) \hspace{0.1cm}{\rm d}\nu .}$$ | + | $$\mathbf{(2)}\hspace{0.5cm}x( t )\left( { - \frac{1}{{{\rm j}\cdot 2\pi t}} + \frac{1}{2}\cdot \delta ( t )} \right)\ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ \ \int_{ - \infty }^f {X( \nu ) \hspace{0.1cm}{\rm d}\nu .}$$}} |
| − | |||
| − | {{ | + | {{BlaueBox|TEXT= |
| + | $\text{Illustration – not an exact proof:}$ | ||
| − | + | The integration theorem represents exactly the inversion of the [[Signal_Representation/Fourier_Transform_Theorems#Differentiation_Theorem|»differentiation theorem«]]. If one applies the differentiation theorem to the equation $\mathbf{(1)}$ one obtains | |
| − | |||
| − | $$\frac{ {\rm d}}{ {\rm d}t} \int_{ - \infty }^{\hspace{0.05cm}t} {x( \tau )} \hspace{0.1cm}{\rm d}\tau\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X( f )\left( {\frac{1}{{{\rm j}2\pi f}} + \frac{1}{2}\cdot \delta ( f )} \right) \cdot {\rm j}2\pi f.$$ | + | :$$\frac{ {\rm d} }{ {\rm d}t} \int_{ - \infty }^{\hspace{0.05cm}t} {x( \tau )} \hspace{0.1cm}{\rm d}\tau\ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\ \ X( f )\cdot \left( {\frac{1}{ { {\rm j}\cdot 2\pi f} } + \frac{1}{2}\cdot \delta ( f )} \right) \cdot {\rm j}\cdot 2\pi f.$$ |
| − | + | This example shows the validity of the integration theorem: | |
| − | + | #The differentiation according to the upper limit on the left side yields exactly the integrand $x(t)$. | |
| − | + | #The right side of the correspondence correctly results in $X(f)$, since the Dirac delta function is hidden with $f=0$ because of the multiplication with $\text{j}\cdot 2\pi f$.}} | |
| − | + | <u>Notes:</u> All theorems shown in this chapter – such as the integration and differentiation theorem – will be elucidated with examples in the $($German language$)$ learning video <br> [[Gesetzmäßigkeiten_der_Fouriertransformation_(Lernvideo)|»Gesetzmäßigkeiten der Fouriertransformation«]] ⇒ "Regularities to the Fourier transform". | |
| − | + | {{GraueBox|TEXT= | |
| − | {{ | + | [[File:P_ID2725__Sig_T_3_3_S8_neu.png|right|frame|Correlation between "rectangle" and "ramp"]] |
| − | + | $\text{Example 8:}$ | |
| − | [[File:P_ID2725__Sig_T_3_3_S8_neu.png|right| | + | The sketched signals $x_1(t)$ and $x_2(t)$ are related as follows: |
| − | |||
| − | $$x_2( t ) = \frac{1}{T}\cdot \int_{ - \infty }^{\hspace{0.05cm}t} {x_1 } ( \tau )\hspace{0.1cm}{\rm d}\tau .$$ | + | :$$x_2( t ) = \frac{1}{T}\cdot \int_{ - \infty }^{\hspace{0.05cm}t} {x_1 } ( \tau )\hspace{0.1cm}{\rm d}\tau .$$ |
| − | + | *Due to the integration theorem the following relation between the spectra applies: | |
| − | $$X_2 ( f ) = \frac{1}{T}\cdot X_1 ( f ) \cdot \left( {\frac{1}{{{\rm j}2\pi f}} + \frac{1}{2}\cdot \delta ( f )} \right).$$ | + | :$$X_2 ( f ) = \frac{1}{T}\cdot X_1 ( f ) \cdot \left( {\frac{1}{{{\rm j}\cdot 2\pi f}} + \frac{1}{2}\cdot \delta ( f )} \right).$$ |
| − | + | *With the spectral function | |
| − | $$X_1 ( f ) = A \cdot T \cdot {\rm | + | :$$X_1 ( f ) = A \cdot T \cdot {\rm sinc}( {fT} ) \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}\pi fT}$$ |
| − | + | :one gets | |
| − | $$X_2 ( f ) = \frac{ {A }}{2}\cdot \delta ( f ) + \frac{ {A \cdot T}}{{2{\rm j}}} \cdot \frac{ {\sin( {\pi fT})}}{{\left( {\pi fT} \right)^2 }} \cdot {\rm e}^{ - {\rm j}\pi fT} | + | :$$X_2 ( f ) = \frac{ {A } }{2}\cdot \delta ( f ) + \frac{ {A \cdot T} }{ {2{\rm j} } } \cdot \frac{ {\sin( {\pi fT}) } }{ {\left( {\pi fT} \right)^2 } } \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}\pi fT}.$$ |
| − | + | *Or after trigonometric transformations: | |
| − | $$X_2 ( f ) = \frac{ {A}}{2}\cdot \delta ( f ) + \frac{ {A \cdot T}}{{( {2\pi fT} )^2 }}\cdot \ | + | :$$X_2 ( f ) = \frac{ {A} }{2}\cdot \delta ( f ) + \frac{ {A \cdot T} }{ { ( {2\pi fT} )^2 } }\cdot \big[ {\cos( {2\pi fT} ) - 1 - {\rm j}\cdot \sin ( {2\pi ft} )} \big].$$ |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | = | + | *It should be noted: |
| + | #The Dirac delta function at $f = 0$ with weight $A/2$ considers the DC component of the ramp function $x_2(t)$. | ||
| + | #This also means: The DC component of the ramp function is exactly the same as the DC component of the jump function. | ||
| + | #The missing triangle with the corner point coordinates $(0, 0)$, $(T, A)$ and $(0, A)$ does not change the DC component. | ||
| + | #This triangular area has no effect compared to the infinite remaining area  $($going to infinity$)$.}} | ||
| − | |||
| − | [[Aufgaben: 3. | + | ==Exercises for the chapter== |
| + | <br> | ||
| + | [[Aufgaben:Exercise 3.4: Trapezoidal Spectrum and Pulse|Exercise 3.4: Trapezoidal Spectrum and Pulse]] | ||
| − | [[Aufgaben:3. | + | [[Aufgaben:Exercise 3.4Z: Trapezoid, Rectangle and Triangle|Exercise 3.4Z: Trapezoid, Rectangle and Triangle]] |
| − | [[Aufgaben: 3. | + | [[Aufgaben:Exercise 3.5: Differentiation of a Triangular Pulse|Exercise 3.5: Differentiation of a Triangular Pulse]] |
| − | [[Aufgaben:3. | + | [[Aufgaben:Exercise 3.5Z: Integration of Dirac Functions|Exercise 3.5Z: Integration of Dirac Functions]] |
| + | [[Aufgaben:Exercise 3.6: Even/Odd Time Signal|Exercise 3.6: Even/Odd Time Signal]] | ||
| + | [[Aufgaben:Exercise 3.6Z: Complex Exponential Function|Exercise 3.6Z: Complex Exponential Function]] | ||
{{Display}} | {{Display}} | ||
Latest revision as of 17:26, 14 June 2023
Contents
Multiplication with a factor - Addition Theorem
In this section the »Fourier Transform Theorems« are assembled. These can be used, for examle, to derive from already known transformations
- $$x( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X( f ),\quad x_1 ( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X_1 ( f ),\quad x_2 ( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X_2 ( f )$$
new functional relationships. Here we restrict ourselves to real time functions.
$\text{Theorem:}$ A $\text{constant factor}$ $k$ affects the time and spectral function in the same way:
- $$k \cdot x(t)\ \;\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\ k \cdot X(f).$$
- This relation can be used for simplification by omitting the constant $k$ $($which can be a gain, an attenuation or a unit factor$)$ and adding it to the result later.
- The above sentence follows directly from the definition of the »first Fourier integral«, as well as from the »addition theorem«, which formulates the foundation of the »superposition principle«.
$\text{Addition Theorem:}$ If a time function can be written as a sum of single functions, the resulting spectral function is the sum of the resulting single spectra:
- $$x( t ) = x_1 ( t ) + x_2 ( t )\quad\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\quad X( f ) = X_1 (f) + X_2 ( f ).$$
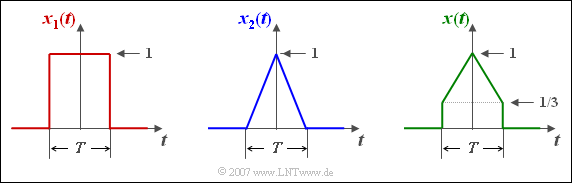
$\text{Example 1:}$ The following Fourier correspondences are known:
- The rectangular pulse:
- $$x_1 ( t )\hspace{0.15cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X_1 ( f )=T \cdot {\rm sinc}(f T),$$
- the triangle pulse:
- $$ x_2 ( t )\hspace{0.15cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X_2 ( f )=T /2\cdot {\rm sinc}^2(f T/2).$$
These two pulses are sketched on the right as red and blue curve respectively.
⇒ Then for the Fourier correspondences of the green drawn $($weighted$)$ sum signal $x(t)$ holds:
- $$x(t) = {1}/{3} \cdot x_1 ( t ) + {2}/{3} \cdot x_2 ( t )\hspace{0.15cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X(f) = {1}/{3} \cdot X_1 ( f ) + {2}/{3} \cdot X_2 ( f ).$$
All theorems presented in this chapter can be found at the following $($German language$)$ learning video with illustrated examples
»Gesetzmäßigkeiten der Fouriertransformation« ⇒ "Regularities to the Fourier transform".
Assignment Theorem
With the »complex Fourier series« for describing periodic signals, we have found
- that an even function always leads to real Fourier coefficients, and
- an odd function exclusively to imaginary Fourier coefficients.
The Fourier transform shows similar properties.
$\text{Assignment Theorem:}$ If a real time function consists additively of an even $($German: "gerade" ⇒ $\text{"g"})$ and an odd $($German: "ungerade" ⇒ $\text{"u"})$ part,
- $$x( t ) = x_{\rm g} ( t ) + x_{\rm u} ( t ),$$
then the following applies for its spectral function:
- $$X(f) = X_{\rm R}(f) + {\rm j}\cdot X_{\rm I}(f), \hspace{0.5cm}\text{with}$$
- $$ x_{\rm g} (t) \hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X_{\rm R}(f),$$
- $$x_{\rm u} (t) \hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} {\rm j} \cdot X_{\rm I} (f).$$
The real part $X_{\rm R}(f)$ of the spectrum is then also even, while $X_{\rm I}(f)$ describes an odd function of frequency.
- The assignment theorem can be easily proved by considering the theorem of »$\text{Leonhard Euler}$«:
- $${\rm e}^{ - {\rm j}\omega _0 t} = \cos ( {\omega _0 t} ) - {\rm j}\cdot \sin ( {\omega _0 t} ).$$
- The even and odd part of each function $x(t)$ can be calculated with the following equations:
- $$x_{\rm g} (t) = {1}/{2}\big[ {x(t) + x(-t)} \big],$$
- $$x_{\rm u} (t) = {1}/{2}\big[ {x(t) - x(-t)} \big].$$
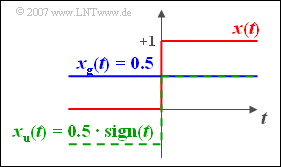
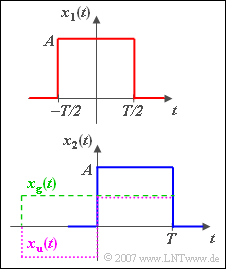
$\text{Example 2:}$ We consider the »jump function«
- $$x(t) = \gamma (t) = \bigg\{ \begin{array}{l} 0\quad \quad {\rm for}\;t < 0 \\ 1\quad \quad{\rm for}\; t > 0 \\ \end{array} ,$$
which can be split as follows:
- $$\gamma (t) = {1}/{2} +{1}/{2} \cdot {\rm sign}(t).$$
The »signum function« was used here:
- $${\rm sign} (t) = \bigg\{ \begin{array}{l} -1\quad \quad {\rm for}\;t < 0, \\ +1\quad \quad{\rm for}\; t > 0. \\ \end{array} $$
Therefore the following applies:
- The even $($blue$)$ signal part $x_{\rm g} (t) = {1}/{2}$ is a constant with the real spectral function $X_{\rm R}(f) = {1}/{2} \cdot \delta(f)$.
- The spectrum ${\rm j} \cdot X_{\rm I}(f)$ of the odd $($green$)$ signum function $x_{\rm u} (t)$ was already calculated in the earlier $\text{Example 3}$ in the section »Fourier transform«.
- This results for the spectrum of the $($red$)$ sketched jump function:
- $$X(f) = X_{\rm R}(f) + {\rm j}\cdot X_{\rm I}(f)= {1}/{2} \cdot \delta (f) - {\rm j}\cdot \frac{1}{2\pi f}.$$
Similarity Theorem
The similarity theorem shows the relation between the spectral functions of two time signals of the same shape, stretched or compressed.
$\text{Similarity Theorem:}$ If $X(f)$ is the Fourier transform of $x(t)$, then with the real constant $k$ the following relation applies:
- $$x( {k \cdot t} )\hspace{0.15cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} \frac{1}{\left \vert \hspace{0.05cm} k\hspace{0.05cm} \right \vert} \cdot X( {f}/{k} ).$$
$\text{Proof:}$ For positive $k$ follows from the Fourier integral with the substitution $\tau = k \cdot t$:
- $$\int_{ - \infty }^{ + \infty } {x( {k \cdot t})} \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}ft} \hspace{0.1cm}{\rm d}t = \frac{1}{k} \cdot \int_{ - \infty }^{ + \infty } {x( \tau )} \cdot {\rm e}^{ - {\rm j}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm} f/k \hspace{0.05cm}\cdot \hspace{0.05cm}\tau } \hspace{0.1cm}{\rm d} \tau = \frac{1}{k}\cdot X( {{f}/{k}}).$$
- For negative $k$ the integration limits would be mixed up and you get $-1/k \cdot X(f/k)$.
- Since in the equation $\vert \hspace{0.05cm} k \hspace{0.05cm} \vert$ is used, the result is valid for both signs.
The effects of the similarity theorem can be illustrated, for example, with an audio tape.
- If such a tape is played with double speed, this corresponds to a compression of the time signal $(k = 2)$.
- Thus the frequencies appear twice as high.
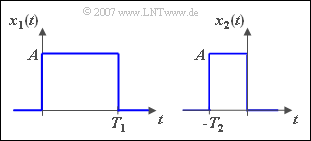
$\text{Example 3:}$ We consider two rectangles of equal height, where $T_2 = T_1/2$ holds.
- The spectral function of $x_1(t)$ results after the »first Fourier Integral« to
- $$X_1 (f) = A \cdot \frac{ {1 - {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 } } }{ { {\rm j}2\pi f} } .$$
- For this can also be written:
- $$X_1 (f) = A \cdot T_1 \cdot \frac{{{\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 } - {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 } }}{{{\rm j}2\pi fT_1 }} \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 } = A \cdot T_1 \cdot {\rm sinc}( {f T_1 } ) \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 }.$$
- For the spectral function of $x_2(t)$ follows from the similarity theorem with $k = -2$:
- $$X_2 (f) = \frac{1}{2} \cdot X_1 ( { - {f}/{2}} ) = \frac{A \cdot T_1 }{2} \cdot {\rm sinc}( { - f {T_1 }/{2} } ) \cdot {\rm e}^{ {\rm j}\pi fT_1 /2} .$$
- The function $\text{sinc}(x) = \sin(x)/x$ is even: $\text{sinc}(-x) = \text{sinc}(x)$. Therefore you can omit the sign in the argument of the $\text{sinc}$–function.
- With $T_2 = T_1/2$ one gets:
- $$X_2 (f) = A \cdot T_2 \cdot {\rm sinc}( {fT_2 } ) \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}T_2 } .$$
Reciprocity Theorem of time duration and bandwidth
This law follows directly from the »similarity theorem«: The wider a pulse is in its extension, the narrower and higher is the corresponding spectrum and vice versa.
- To be able to make quantitative statements, we define two parameters for energy-limited signals. Both quantities are shown in the diagram in $\text{Example 4}$ for a Gaussian pulse and its likewise Gaussian spectrum.
$\text{Definition:}$ The »equivalent pulse duration« is derived from the time course. It is equal to the width of an area–equal rectangle with same height as $x(t)$:
- $$\Delta t = \frac{1}{{x( {t = 0} )}} \cdot \int_{ - \infty }^{ + \infty } {x( t)} \hspace{0.1cm}{\rm d}t.$$
$\text{Definition:}$ The »equivalent bandwidth« is defined in the frequency domain. It gives the width of the area–equal rectangle with same height as spectrum $X(f)$:
- $$\Delta f = \frac{1}{{X( {f = 0} )}}\cdot \int_{ - \infty }^{ + \infty } {X( f )} \hspace{0.1cm} {\rm d}f.$$
$\text{Reciprocity Theorem:}$ The product of the equivalent pulse duration and the equivalent bandwidth is always the same $1$:
- $$\Delta t \cdot \Delta f = 1.$$
$\text{Proof:}$ Based on the two Fourier integrals, for $f = 0$ resp. $t = 0$:
- $$X( {f = 0} ) = \int_{ - \infty }^{ + \infty } {x(t)\hspace{0.1cm}{\rm d}t,}$$
- $$x( {t = 0} ) = \int_{ - \infty }^{ + \infty } {X(f)\hspace{0.1cm}{\rm d}f.}$$
If you take this result into account in the above definitions, you get
- $$\Delta t = \frac{{X( {f = 0} )}}{{x( {t = 0} )}}, \hspace{0.5cm}\Delta f = \frac{{x( {t = 0} )}}{{X( {f = 0} )}}.$$
Note that $\Delta f$ is defined over the actual spectrum $X(f)$ and not over $|X(f)|$.
- For real functions the integration over the even function part is sufficient, since the integral over the odd part is always zero due to the »assignment theorem«.
- For odd time functions and thus purely imaginary spectra, the two definitions of $\Delta t$ and $\Delta f$ fail.
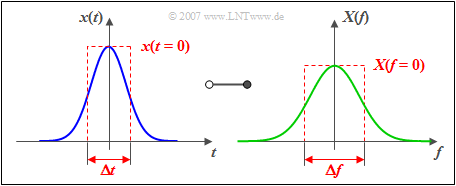
$\text{Example 4:}$ The graph illustrates the equivalent pulse duration $\Delta t$ and the equivalent bandwidth $\Delta f$ exemplary for the Gaussian pulse.
Furthermore, it is valid:
- Widening the Gaussian pulse by the factor $3$ will reduce the equivalent bandwidth by the same factor.
- If the pulse amplitude $x(t = 0)$ is not changed, the integral area above $X(f)$ remains constant.
- This means that $X(f=0)$ is simultaneously increased by the factor $3$ .
Duality Theorem
This regularity is particularly useful for obtaining new Fourier correspondences.
$\text{Duality Theorem:}$ If $X(f)$ is the Fourier transform of $x(t)$, then:
- $$X^{\star}(t)\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}x^{\star}( f ).$$
If we restrict ourselves to real time functions, the signs for »conjugated complex» can be omitted on both sides of the Fourier correspondence.
$\text{Proof:}$ The »first Fourier integral« is after successive renaming $t \to u$, $f \to t$:
- $$X( f ) = \int_{ - \infty }^{ + \infty } {x( u )} \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}u} \hspace{0.1cm}{\rm d}u, \hspace{1cm} X(t ) = \int_{ - \infty }^{ + \infty } {x( u )} \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}t\hspace{0.05cm}\cdot \hspace{0.05cm}u}\hspace{0.1cm} {\rm d}u.$$
- If you change the sign in the exponent, you have to replace $X(t)$ by $X^*(t)$ and $x(u)$ by $x^*(u)$ :
- $$X^{\star}(t ) = \int_{ - \infty }^{ + \infty } {x^{\star}( u )} \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi\hspace{0.05cm}\cdot \hspace{0.05cm} t\hspace{0.05cm}\cdot \hspace{0.05cm}u}\hspace{0.1cm} {\rm d}u.$$
- With the further renaming $u \to f$ one gets to the »second Fourier integral«:
- $$X^{\star}(t ) = \int_{ - \infty }^{ + \infty } {x^{\star}( f )} \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}f.\hspace{7.9cm}$$
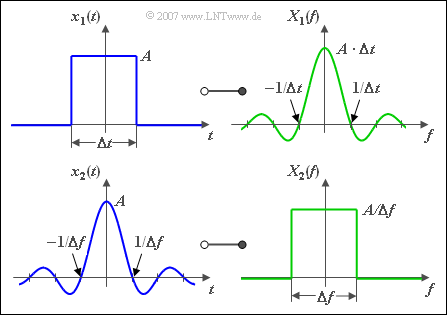
$\text{Example 5:}$
The figure on the right shows an application of the duality theorem, namely the functional relations between
- a signal $x_1(t)$ with rectangular time function, and
- a signal $x_2(t)$ with rectangular spectral function.
$\text{Another Example:}$
- The spectrum $X(f) = \delta(f)$ of the DC signal $x(t) = 1$ is assumed to be known.
- According to the »duality theorem«, the spectral function of the Dirac delta is therefore:
- $$ x(t) = \delta(t)\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X(f)= 1.$$
Shifting Theorem
We now consider
- a shift of the time function, e.g. caused by a delay;
- or a frequency shift, as it occurs for example with »analog double-sideband amplitude modulation«.
$\text{Shifting Theorem:}$ If $X(f)$ is the Fourier transform of $x(t)$, the following correspondences also apply:
$$\mathbf{(1)}\hspace{0.5cm}x( {t - t_0 } )\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X( f ) \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm} f\hspace{0.05cm}\cdot \hspace{0.05cm}t_0 },$$
$$\mathbf{(2)}\hspace{0.5cm}x( t ) \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_0 \hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X( {f - f_0 } ).$$
Here, $t_0$ and $f_0$ are any time or frequency values.
$\text{Proof of Equation (1):}$ The »first Fourier integral« for signal $x_{\rm V}(t) = x(t-t_0)$ shifted to the right by $t_0$ is defined with the substitution $\tau = t - t_0$:
- $$X_{\rm V} ( f ) = \int_{ - \infty }^{ + \infty } {x( {t - t_0 } ) \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm}{\rm d}t} = \int_{ - \infty }^{ + \infty } {x( \tau ) \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}( {\tau + t_0 } )}\hspace{0.1cm} {\rm d}\tau .}$$
- The term independent from the integration variable $\tau$ can be dragged in front of the integral.
- With the renaming $\tau \to t$ one then obtains
- $$X_{\rm V}( f ) = {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}t_0 } \cdot \int_{ - \infty }^{ + \infty } {x( t )} \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}t = {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}t_0 } \cdot X( f).$$
$\text{Example 6:}$ As already mentioned, the symmetrical rectangular pulse $x_1(t)$ has the spectrum
- $$X_1 ( f ) = A \cdot T \cdot {\rm si}( {\pi fT} )= A \cdot T \cdot {\rm sinc}( {fT} )$$
- $$\hspace{0.9cm} \text{with} \hspace{0.5cm} {\rm si}(x)= \sin(x)/x,\hspace{0.5cm}{\rm sinc}(x)= \sin(\pi x)/(\pi x)={\rm si}(x/\pi).$$
- The rectangular pulse $x_2(t)$ displayed below is shifted to the right with respect to $x_1(t)$ by $T/2$:
- $$x_2(t) = x_1(t-T/2).$$
- Thus its spectrum is:
- $$X_2( f ) = A \cdot T \cdot {\rm sinc}( {fT} ) \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}T} .$$
- This spectral function can also be written as follows with the »theorem of Euler« and some trigonometric conversions:
- $$X_2( f ) = \frac{A }{2\pi f} \cdot \sin ( 2\pi fT) + {\rm j}\cdot \frac{A }{2\pi f} \cdot \big[ {\cos ( {2\pi fT} ) - 1} \big] .$$
- The same result can be obtained with the »assignment theorem«;
⇒ The real part of the spectrum belongs to the even signal part $x_{\rm g}(t)$, the imaginary part to the odd signal part $x_{\rm u}(t)$.
Differentiation Theorem
This theorem shows, how the differentiation of a function $x(t)$ resp. $X(f)$ affects the corresponding Fourier transform; it is also applicable several times.
A simple example for the application of this theorem is the relation between current $i(t)$ and voltage $u(t)$ of a capacitance $C$ according to the equation
- $$i(t) = C \cdot \text{d}u(t)/\text{d}t.$$
$\text{Differentiation Theorem:}$ If $X(f)$ is the Fourier transform of $x(t)$, the following two correspondences are also valid:
$$\mathbf{(1)}\hspace{0.5cm}\frac{{{\rm d}x( t )}}{{{\rm d}t}}\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi f \cdot X( f ),$$
$$\mathbf{(2)}\hspace{0.5cm}- t \cdot x( t )\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}\frac{1}{{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi }} \cdot \frac{{{\rm d}X( f )}}{{{\rm d}f}}.$$
$\text{Proof of Equation (1):}$ This equation results from differentiation of the »second Fourier integral«:
- $$y(t) = \frac{\text{d}x(t)}{\text{d}t} = \frac{\text{d} }{\text{d}t}\int_{ - \infty }^{ + \infty } X( f ) \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\hspace{0.03cm}\pi\hspace{0.05cm}\cdot \hspace{0.05cm} f\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}f = \int_{ - \infty }^{ + \infty } {X( f )} \cdot {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi f \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm} f\hspace{0.05cm}\cdot \hspace{0.05cm}t} {\rm d}f.$$
At the same time is:
- $$y( t ) = \int_{ - \infty }^{ + \infty } {Y( f )} \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\hspace{0.03cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}f.$$
- By comparing the integrands, the variation $\mathbf{(1)}$ of the differentiation theorem is obtained.
- To derive the second variant one proceeds from the »first Fourier integral« in an analogous manner.
- The negative exponent in the first Fourier integral leads to the minus sign in the time function. q.e.d.
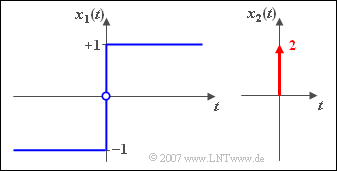
$\text{Example 7:}$ The spectra of the signals $x_1(t)$ and $x_2(t)$ were already calculated in the previous examples:
- $$X_1( f ) = \frac{1 }{ {\rm j\cdot \pi} f}, $$
- $$X_2( f ) = 2 = {\rm const.}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} X_2(f) = X_1(f) \cdot {\rm j}\cdot 2\pi f.$$
- From the differentiation theorem it follows that $x_2(t)$ is equal to the time-derivative of $x_1(t)$ .
- This is actually correct: For $t \neq 0$ ⇒ $x_1(t)$ is constant, i.e. the derivative is zero.
- For $t=0$ the gradient is infinitely large, which is also expressed in the equation $x_2(t) = 2 \cdot \delta(t)$.
- The impulse weight "$2$" of $x_2(t)$ considers that the jump within $x_1(t)$ at $t = 0$ has the height "$2$".
Integration Theorem
Integration is just like differentiation a linear operation. This results in the following theorem:
$\text{Integration Theorem:}$ If $X(f)$ is the Fourier transform $($spectral function$)$ of $x(t)$, then the following Fourier correspondences also apply:
$$\mathbf{(1)}\hspace{0.5cm}\int_{ - \infty }^{\hspace{0.05cm}t} {x( \tau )} \hspace{0.1cm}{\rm d}\tau \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ \ X( f )\left( {\frac{1}{{{\rm j}\cdot 2\pi f}} + \frac{1}{2}\cdot \delta ( f )} \right),$$
$$\mathbf{(2)}\hspace{0.5cm}x( t )\left( { - \frac{1}{{{\rm j}\cdot 2\pi t}} + \frac{1}{2}\cdot \delta ( t )} \right)\ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ \ \int_{ - \infty }^f {X( \nu ) \hspace{0.1cm}{\rm d}\nu .}$$
$\text{Illustration – not an exact proof:}$
The integration theorem represents exactly the inversion of the »differentiation theorem«. If one applies the differentiation theorem to the equation $\mathbf{(1)}$ one obtains
- $$\frac{ {\rm d} }{ {\rm d}t} \int_{ - \infty }^{\hspace{0.05cm}t} {x( \tau )} \hspace{0.1cm}{\rm d}\tau\ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\ \ X( f )\cdot \left( {\frac{1}{ { {\rm j}\cdot 2\pi f} } + \frac{1}{2}\cdot \delta ( f )} \right) \cdot {\rm j}\cdot 2\pi f.$$
This example shows the validity of the integration theorem:
- The differentiation according to the upper limit on the left side yields exactly the integrand $x(t)$.
- The right side of the correspondence correctly results in $X(f)$, since the Dirac delta function is hidden with $f=0$ because of the multiplication with $\text{j}\cdot 2\pi f$.
Notes: All theorems shown in this chapter – such as the integration and differentiation theorem – will be elucidated with examples in the $($German language$)$ learning video
»Gesetzmäßigkeiten der Fouriertransformation« ⇒ "Regularities to the Fourier transform".
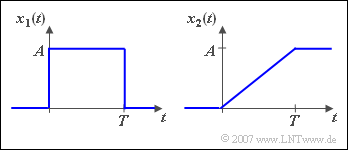
$\text{Example 8:}$ The sketched signals $x_1(t)$ and $x_2(t)$ are related as follows:
- $$x_2( t ) = \frac{1}{T}\cdot \int_{ - \infty }^{\hspace{0.05cm}t} {x_1 } ( \tau )\hspace{0.1cm}{\rm d}\tau .$$
- Due to the integration theorem the following relation between the spectra applies:
- $$X_2 ( f ) = \frac{1}{T}\cdot X_1 ( f ) \cdot \left( {\frac{1}{{{\rm j}\cdot 2\pi f}} + \frac{1}{2}\cdot \delta ( f )} \right).$$
- With the spectral function
- $$X_1 ( f ) = A \cdot T \cdot {\rm sinc}( {fT} ) \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}\pi fT}$$
- one gets
- $$X_2 ( f ) = \frac{ {A } }{2}\cdot \delta ( f ) + \frac{ {A \cdot T} }{ {2{\rm j} } } \cdot \frac{ {\sin( {\pi fT}) } }{ {\left( {\pi fT} \right)^2 } } \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}\pi fT}.$$
- Or after trigonometric transformations:
- $$X_2 ( f ) = \frac{ {A} }{2}\cdot \delta ( f ) + \frac{ {A \cdot T} }{ { ( {2\pi fT} )^2 } }\cdot \big[ {\cos( {2\pi fT} ) - 1 - {\rm j}\cdot \sin ( {2\pi ft} )} \big].$$
- It should be noted:
- The Dirac delta function at $f = 0$ with weight $A/2$ considers the DC component of the ramp function $x_2(t)$.
- This also means: The DC component of the ramp function is exactly the same as the DC component of the jump function.
- The missing triangle with the corner point coordinates $(0, 0)$, $(T, A)$ and $(0, A)$ does not change the DC component.
- This triangular area has no effect compared to the infinite remaining area  $($going to infinity$)$.
Exercises for the chapter
Exercise 3.4: Trapezoidal Spectrum and Pulse
Exercise 3.4Z: Trapezoid, Rectangle and Triangle
Exercise 3.5: Differentiation of a Triangular Pulse
Exercise 3.5Z: Integration of Dirac Functions
Exercise 3.6: Even/Odd Time Signal
Exercise 3.6Z: Complex Exponential Function