Difference between revisions of "Aufgaben:Exercise 4.14: Phase Progression of the MSK"
m |
|||
| (30 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Modulationsverfahren/Nichtlineare_digitale_Modulation |
}} | }} | ||
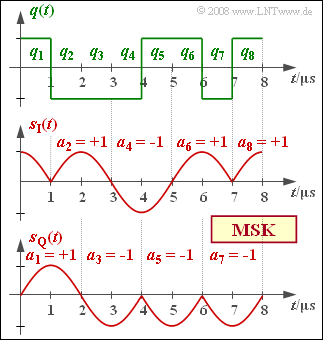
| − | [[File:P_ID1740__Mod_A_4_13.png|right|]] | + | [[File:P_ID1740__Mod_A_4_13.png|right|frame|Source signal and low-pass signals <br>in both branches of the MSK]] |
| − | + | One possible implementation of ''Minimum Shift Keying'' $\rm (MSK)$ is offered by $\rm Offset–QPSK$, as shown in the [[Modulation_Methods/Nonlinear_Digital_Modulation#Realizing_MSK_as_Offset.E2.80.93QPSK|block diagram]] in the theory section. | |
| + | *For this, a recoding of the source symbols $q_k ∈ \{+1, –1\}$ into the similarly binary amplitude coefficients $a_k ∈ \{+1, –1\}$ must first be undertaken. | ||
| + | *This recoding is discussed in detail in [[Aufgaben:Exercise_4.14Z:_Offset_QPSK_vs._MSK|Exercise 4.14Z]] . | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | The graph shows the two equivalent low-pass signals $s_{\rm I}(t)$ and $s_{\rm Q}(t)$ in the two branches below, which are obtained for the inphase and quadrature branches after recoding $a_k = (-1)^{k+1} \cdot a_{k-1} \cdot q_k $ from the source signal $q(t)$ sketched above. Considered here is the MSK fundamental pulse, |
| + | :$$ g_{\rm MSK}(t) = \left\{ \begin{array}{l} \cos \big ({\pi \hspace{0.05cm} t}/({2 \hspace{0.05cm} T})\big ) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{for}} \\{\rm{for}} \\ \end{array}\begin{array}{*{10}c} -T \le t \le +T \hspace{0.05cm}, \\ {\rm otherwise}\hspace{0.05cm}. \\ \end{array}$$ | ||
| + | This is normalized to $1$ , as are the signals $s_{\rm I}(t)$ and $s_{\rm Q}(t)$ . | ||
| + | |||
| + | In keeping with the chapter [[Signal_Representation/Equivalent_Low_Pass_Signal_and_Its_Spectral_Function|Equivalent Low-Pass Signal and its Spectral Function]] in the book "Signal Representation", the equivalent low-pass signal is: | ||
| + | :$$ s_{\rm TP}(t) = s_{\rm I}(t) + {\rm j} \cdot s_{\rm Q}(t) = |s_{\rm TP}(t)| \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}\phi(t)}\hspace{0.05cm},$$ | ||
| + | *with magnitude | ||
| + | :$$|s_{\rm TP}(t)| = \sqrt{s_{\rm I}^2(t) + s_{\rm Q}^2(t)} $$ | ||
| + | *and phase | ||
| + | :$$ \phi(t) = {\rm arc} \hspace{0.15cm}s_{\rm TP}(t) = {\rm arctan}\hspace{0.1cm} \frac{s_{\rm Q}(t)}{s_{\rm I}(t)} \hspace{0.05cm}.$$ | ||
| + | The physical MSK transmitted signal is then given by | ||
| + | :$$ s(t) = |s_{\rm TP}(t)| \cdot \cos (2 \pi \cdot f_{\rm T} \cdot t + \phi(t)) \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Hints:'' | ||
| + | *This exercise belongs to the chapter [[Modulation_Methods/Nonlinear_Digital_Modulation|Nonlinear Digital Modulation]]. | ||
| + | *Particular reference is made to the section [[Modulation_Methods/Nonlinear_Digital_Modulation#Realizing_MSK_as_Offset.E2.80.93QPSK|Realizing MSK as Offset–QPSK]]. | ||
| + | |||
| + | *Assume $ϕ(t = 0) = ϕ_0 = 0$ . | ||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which statements are true for the envelope curve $|s_{\rm TP}(t)|$ of MSK? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - The envelope curve is a cosine oscillation. |
| − | + | + | + The envelope curve is constant. |
| − | + | + | + The envelope curve is independent of the transmitted sequence. |
| − | { | + | {Let $T = 1 \ \rm µs$. Calculate the phase response in the interval $0 ≤ t ≤ T$. |
| + | <br>What are the phase values for $t = T/2$ and $t = T$? | ||
|type="{}"} | |type="{}"} | ||
| − | $ϕ(t = T/2)$ | + | $ϕ(t = T/2)\ = \ $ { 45 3% } $\ \rm degrees$ |
| − | $ϕ(t = T)$ | + | $ϕ(t = T) \hspace{0.63cm} = \ ${ 90 3% } $\ \rm degrees$ |
| − | { | + | {Determine the phase values at $t = 2T$, $t = 3T$ and $t = 4T$. |
|type="{}"} | |type="{}"} | ||
| − | $ϕ(t = 2T)$ | + | $ϕ(t = 2T) \ = \ $ { 0. } $\ \rm degrees$ |
| − | $ϕ(t = 3T)$ | + | $ϕ(t = 3T) \ = \ $ { -92.7--87.3 } $\ \rm degrees$ |
| − | $ϕ(t = 4T)$ | + | $ϕ(t = 4T) \ = \ $ { -185.4--174.6 } $\ \rm degrees$ |
| − | { | + | {Sketch and interpret the phase response $ϕ(t)$ in the range from $0$ to $8T$. <br>What are the phase values at the following times? |
|type="{}"} | |type="{}"} | ||
| − | $ϕ(5T)$ | + | $ϕ(t = 5T) \ = \ $ { -92.7--87.3 } $\ \rm degrees$ |
| − | $ϕ(6T)$ | + | $ϕ(t = 6T) \ = \ $ { 0. } $\ \rm degrees$ |
| − | $ϕ(7T)$ | + | $ϕ(t = 7T) \ = \ $ { -92.7--87.3 } $\ \rm degrees$ |
| − | $ϕ(8T)$ | + | $ϕ(t = 8T) \ = \ $ { 0. } $\ \rm degrees$ |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1.''' | + | '''(1)''' <u>Answers 2 and 3</u> are correct: |
| + | *For example, in the range $0 ≤ t ≤ T$, considering that $a_0^2 = a_1^2 = 1$ : | ||
| + | :$$ |s_{\rm TP}(t)| = \sqrt{a_0^2 \cdot \cos^2 (\frac{\pi \cdot t}{2 \cdot T}) + a_1^2 \cdot \sin^2 (\frac{\pi \cdot t}{2 \cdot T})} = 1 \hspace{0.05cm}.$$ | ||
| + | *Thus, statement 2 is correct, while statement 1 is false. | ||
| + | *This result holds for any pair of values $a_0 ∈ \{+1, \ –1\}$ and $a_1 ∈ \{+1, \ –1\}$. | ||
| + | *From this, it can be further concluded that the envelope is independent of the transmitted sequence. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' With the given equation, it holds that: | ||
| + | :$$\phi(t) = {\rm arctan}\hspace{0.1cm} \frac{s_{\rm Q}(t)}{s_{\rm I}(t)} = {\rm arctan}\hspace{0.1cm} \frac{a_1 \cdot \sin (\frac{\pi \cdot t}{2 \cdot T})}{a_0 \cdot \cos (\frac{\pi \cdot t}{2 \cdot T})}= {\rm arctan}\hspace{0.1cm}\left [ \frac{a_1}{a_0}\cdot \tan \hspace{0.1cm}(\frac{\pi \cdot t}{2 \cdot T})\right ] \hspace{0.05cm}.$$ | ||
| + | *The quotient $a_1/a_0$ is always $+1$ or $-1$. Thus, this quotient is preferable and we get: | ||
| + | :$$\phi(t) = \frac{a_1}{a_0}\cdot {\rm arctan}\hspace{0.1cm}\left [ | ||
| + | \tan \hspace{0.1cm}(\frac{\pi \cdot t}{2 \cdot T})\right ]= \frac{a_1}{a_0}\cdot \frac{\pi \cdot t}{2 \cdot T} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | *The initial phase $ϕ_0 = 0$ can rule out ambiguities. In particular, because $a_0 = a_1 = +1$: | ||
| + | :$$\phi(t = T/2 = 0.5\,{\rm µ s}) = {\pi}/{4}\hspace{0.15cm}\underline { = +45^\circ},\hspace{0.2cm}\phi(t = T= 1\,{\rm µ s}) = {\pi}/{2}\hspace{0.15cm}\underline {= +90^\circ} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(3)''' The easiest way to solve this problem is to use the unit circle: | ||
| + | :$$ {\rm Re} = s_{\rm I}(2T) = +1, \hspace{0.2cm} {\rm Im} = s_{\rm Q}(2T) = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\phi(t = 2T= 2\,{\rm µ s}) \hspace{0.15cm}\underline {= 0^\circ},$$ | ||
| + | :$$ {\rm Re} = s_{\rm I}(3T) = 0, \hspace{0.2cm} {\rm Im} = s_{\rm Q}(3T) = -1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\phi(t = 3T= 3\,{\rm µ s}) \hspace{0.15cm}\underline {= -90^\circ},$$ | ||
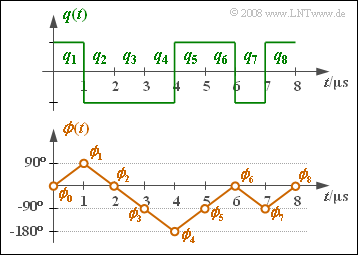
| + | [[File:P_ID1741__Mod_A_4_13_d.png|right|frame|Source signal and phase response in MSK]] | ||
| + | :$${\rm Re} = s_{\rm I}(4T) = -1, \hspace{0.2cm} {\rm Im} = s_{\rm Q}(4T) = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\phi(t = 4T= 4\,{\rm µ s})= \pm 180^\circ \hspace{0.05cm}.$$ | ||
| − | + | *From the sketch below, we can see that $\phi(t = 4T= 4\,{\rm µ s})\hspace{0.15cm}\underline { = - 180^\circ}\hspace{0.05cm}$ is correct. | |
| − | $ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | '''(4)''' The graph shows the MSK phase $ϕ(t)$ together with the source signal $q(t)$. It can be seen that: | ||
| + | * At symbol $a_\nu =+1$ the phase increases linearly by $90^\circ \ (π/2)$ within the symbol duration $T$ . | ||
| + | * At symbol $a_\nu =-1$ the phase decreases linearly by $90^\circ \ (π/2)$ within the symbol duration $T$ . | ||
| + | *Thus, the remaining phase values are: | ||
| + | :$$\phi(5T) \hspace{0.15cm}\underline { = -90^\circ},\hspace{0.2cm}\phi(t = 6T) \hspace{0.15cm}\underline {= 0^\circ} \hspace{0.05cm}.$$ | ||
| + | :$$ \phi(7T)\hspace{0.15cm}\underline { = -90^\circ},\hspace{0.2cm} \phi(t = 8T) \hspace{0.15cm}\underline {= 0^\circ} \hspace{0.05cm}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Modulation Methods: Exercises|^4.4 Non-linear Digital Modulation^]] |
Latest revision as of 12:37, 21 March 2022
One possible implementation of Minimum Shift Keying $\rm (MSK)$ is offered by $\rm Offset–QPSK$, as shown in the block diagram in the theory section.
- For this, a recoding of the source symbols $q_k ∈ \{+1, –1\}$ into the similarly binary amplitude coefficients $a_k ∈ \{+1, –1\}$ must first be undertaken.
- This recoding is discussed in detail in Exercise 4.14Z .
The graph shows the two equivalent low-pass signals $s_{\rm I}(t)$ and $s_{\rm Q}(t)$ in the two branches below, which are obtained for the inphase and quadrature branches after recoding $a_k = (-1)^{k+1} \cdot a_{k-1} \cdot q_k $ from the source signal $q(t)$ sketched above. Considered here is the MSK fundamental pulse,
- $$ g_{\rm MSK}(t) = \left\{ \begin{array}{l} \cos \big ({\pi \hspace{0.05cm} t}/({2 \hspace{0.05cm} T})\big ) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{for}} \\{\rm{for}} \\ \end{array}\begin{array}{*{10}c} -T \le t \le +T \hspace{0.05cm}, \\ {\rm otherwise}\hspace{0.05cm}. \\ \end{array}$$
This is normalized to $1$ , as are the signals $s_{\rm I}(t)$ and $s_{\rm Q}(t)$ .
In keeping with the chapter Equivalent Low-Pass Signal and its Spectral Function in the book "Signal Representation", the equivalent low-pass signal is:
- $$ s_{\rm TP}(t) = s_{\rm I}(t) + {\rm j} \cdot s_{\rm Q}(t) = |s_{\rm TP}(t)| \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}\phi(t)}\hspace{0.05cm},$$
- with magnitude
- $$|s_{\rm TP}(t)| = \sqrt{s_{\rm I}^2(t) + s_{\rm Q}^2(t)} $$
- and phase
- $$ \phi(t) = {\rm arc} \hspace{0.15cm}s_{\rm TP}(t) = {\rm arctan}\hspace{0.1cm} \frac{s_{\rm Q}(t)}{s_{\rm I}(t)} \hspace{0.05cm}.$$
The physical MSK transmitted signal is then given by
- $$ s(t) = |s_{\rm TP}(t)| \cdot \cos (2 \pi \cdot f_{\rm T} \cdot t + \phi(t)) \hspace{0.05cm}.$$
Hints:
- This exercise belongs to the chapter Nonlinear Digital Modulation.
- Particular reference is made to the section Realizing MSK as Offset–QPSK.
- Assume $ϕ(t = 0) = ϕ_0 = 0$ .
Questions
Solution
- For example, in the range $0 ≤ t ≤ T$, considering that $a_0^2 = a_1^2 = 1$ :
- $$ |s_{\rm TP}(t)| = \sqrt{a_0^2 \cdot \cos^2 (\frac{\pi \cdot t}{2 \cdot T}) + a_1^2 \cdot \sin^2 (\frac{\pi \cdot t}{2 \cdot T})} = 1 \hspace{0.05cm}.$$
- Thus, statement 2 is correct, while statement 1 is false.
- This result holds for any pair of values $a_0 ∈ \{+1, \ –1\}$ and $a_1 ∈ \{+1, \ –1\}$.
- From this, it can be further concluded that the envelope is independent of the transmitted sequence.
(2) With the given equation, it holds that:
- $$\phi(t) = {\rm arctan}\hspace{0.1cm} \frac{s_{\rm Q}(t)}{s_{\rm I}(t)} = {\rm arctan}\hspace{0.1cm} \frac{a_1 \cdot \sin (\frac{\pi \cdot t}{2 \cdot T})}{a_0 \cdot \cos (\frac{\pi \cdot t}{2 \cdot T})}= {\rm arctan}\hspace{0.1cm}\left [ \frac{a_1}{a_0}\cdot \tan \hspace{0.1cm}(\frac{\pi \cdot t}{2 \cdot T})\right ] \hspace{0.05cm}.$$
- The quotient $a_1/a_0$ is always $+1$ or $-1$. Thus, this quotient is preferable and we get:
- $$\phi(t) = \frac{a_1}{a_0}\cdot {\rm arctan}\hspace{0.1cm}\left [ \tan \hspace{0.1cm}(\frac{\pi \cdot t}{2 \cdot T})\right ]= \frac{a_1}{a_0}\cdot \frac{\pi \cdot t}{2 \cdot T} \hspace{0.05cm}.$$
- The initial phase $ϕ_0 = 0$ can rule out ambiguities. In particular, because $a_0 = a_1 = +1$:
- $$\phi(t = T/2 = 0.5\,{\rm µ s}) = {\pi}/{4}\hspace{0.15cm}\underline { = +45^\circ},\hspace{0.2cm}\phi(t = T= 1\,{\rm µ s}) = {\pi}/{2}\hspace{0.15cm}\underline {= +90^\circ} \hspace{0.05cm}.$$
(3) The easiest way to solve this problem is to use the unit circle:
- $$ {\rm Re} = s_{\rm I}(2T) = +1, \hspace{0.2cm} {\rm Im} = s_{\rm Q}(2T) = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\phi(t = 2T= 2\,{\rm µ s}) \hspace{0.15cm}\underline {= 0^\circ},$$
- $$ {\rm Re} = s_{\rm I}(3T) = 0, \hspace{0.2cm} {\rm Im} = s_{\rm Q}(3T) = -1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\phi(t = 3T= 3\,{\rm µ s}) \hspace{0.15cm}\underline {= -90^\circ},$$
- $${\rm Re} = s_{\rm I}(4T) = -1, \hspace{0.2cm} {\rm Im} = s_{\rm Q}(4T) = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\phi(t = 4T= 4\,{\rm µ s})= \pm 180^\circ \hspace{0.05cm}.$$
- From the sketch below, we can see that $\phi(t = 4T= 4\,{\rm µ s})\hspace{0.15cm}\underline { = - 180^\circ}\hspace{0.05cm}$ is correct.
(4) The graph shows the MSK phase $ϕ(t)$ together with the source signal $q(t)$. It can be seen that:
- At symbol $a_\nu =+1$ the phase increases linearly by $90^\circ \ (π/2)$ within the symbol duration $T$ .
- At symbol $a_\nu =-1$ the phase decreases linearly by $90^\circ \ (π/2)$ within the symbol duration $T$ .
- Thus, the remaining phase values are:
- $$\phi(5T) \hspace{0.15cm}\underline { = -90^\circ},\hspace{0.2cm}\phi(t = 6T) \hspace{0.15cm}\underline {= 0^\circ} \hspace{0.05cm}.$$
- $$ \phi(7T)\hspace{0.15cm}\underline { = -90^\circ},\hspace{0.2cm} \phi(t = 8T) \hspace{0.15cm}\underline {= 0^\circ} \hspace{0.05cm}.$$