Difference between revisions of "Aufgaben:Exercise 5.3Z: Realization of a PN Sequence"
From LNTwww
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Modulationsverfahren/Spreizfolgen für CDMA }} [[File:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Choice Frage |ty…“) |
|||
| (29 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Modulation_Methods/Spreading_Sequences_for_CDMA |
}} | }} | ||
| − | [[File:|right|]] | + | [[File:EN_Mod_Z_5_3neu.png|right|frame|Two PN generator realizations]] |
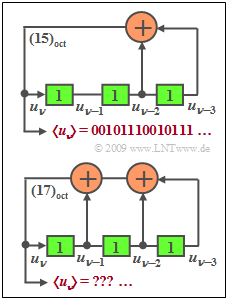
| + | The diagram shows two possible generators for generating PN sequences in unipolar representation: $u_ν ∈ \{0, 1\}$. | ||
| + | *The upper generator with the coefficients | ||
| + | :$$ g_0 = 1 \hspace{0.05cm}, \hspace{0.2cm}g_1 = 0 \hspace{0.05cm}, \hspace{0.2cm}g_2 = 1 \hspace{0.05cm}, \hspace{0.2cm}g_3 = 1 \hspace{0.05cm}$$ | ||
| + | :is denoted by the octal identifier $(g_3,\ g_2,\ g_1,\ g_0)_{\rm octal} = (15)$. | ||
| + | *Accordingly, the octal identifier of the second PN generator is $(17)$. | ||
| − | === | + | *One speaks of an M-sequence if for the period length of the sequence $〈u_ν〉$ holds: |
| + | :$$P = 2^G – 1.$$ | ||
| + | :Here, $G$ denotes the degree of the shift register, which is equal to the number of memory cells. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Notes: | ||
| + | *The exercise belongs to the chapter [[Modulation_Methods/Spreading_Sequences_for_CDMA|Spreading Sequences for CDMA]]. | ||
| + | *Reference is also made to the chapter [[Theory_of_Stochastic_Signals/Erzeugung_von_diskreten_Zufallsgr%C3%B6%C3%9Fen |Generation of Discrete Random Variables]] in the book "Theory of Stochastic Signals". | ||
| + | * We would also like to draw your attention to the (German language) learning video <br> [[Erläuterung_der_PN–Generatoren_an_einem_Beispiel_(Lernvideo)|Erläuterung der PN–Generatoren an einem Beispiel]] ⇒ "Explanation of PN generators using an example". | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the degree $G$ of the two PN generators considered here? |
| + | |type="{}"} | ||
| + | $G \ = \ $ { 3 } | ||
| + | |||
| + | {Give the period length $P$ of the PN generator with the octal identifier $(15)$. | ||
| + | |type="{}"} | ||
| + | $P\ = \ $ { 7 } | ||
| + | |||
| + | {Which of the following statements are true for each M-sequence? | ||
|type="[]"} | |type="[]"} | ||
| − | - | + | - The number of "zeros" and "ones" is the same. |
| − | + | + | + In each period there is one more "ones" than "zeros". |
| + | + The maximum number of consecutive "ones" is $G$. | ||
| + | + The sequence $1 0 1 0 1 0$ ... is not possible. | ||
| − | + | {Specify the period length $P$ of the PN generator with the octal identifier $(17)$. | |
| − | { | ||
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $P\ = \ $ { 1 } |
| − | |||
| + | {Which PN generator produces an M-sequence? | ||
| + | |type="[]"} | ||
| + | + The generator with the octal identifier $(15)$. | ||
| + | - The generator with the octal identifier $(17)$. | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' The degree $\underline{G = 3}$ is equal to the number of memory cells of the shift register. |
| − | '''2 | + | |
| − | '''3 | + | |
| − | '''4 | + | '''(2)''' From the given sequence the period length $\underline{P = 7}$ can be read. Because of $P = 2^G –1$ it is an M-sequence. |
| − | '''5 | + | |
| − | + | ||
| − | + | '''(3)''' <u>Solutions 2, 3 and 4</u> are correct: | |
| + | *The maximum number of consecutive "ones" is $G$ (whenever there is a "one" in all $G$ memory cells). | ||
| + | *On the other hand, it is not possible that all memory cells are filled with zeros (otherwise only zeros would be generated). | ||
| + | *Therefore, there is always one more "ones" than zeros. | ||
| + | *The period length of the sequence "$1 0 1 0 1 0$ ..." is $P = 2$. For an M-sequence $P = 2^G –1$. For no value of $G$: $P = 2$ is possible. | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' If all memory cells are occupied with ones, the generator with the octal identifier $(17)$ returns a $1$ again: | ||
| + | :$$u_{\nu} \big [ u_{\nu-1} + u_{\nu-2} + u_{\nu-3} \big ] \,\,{\rm mod} \,\,2 =1 \hspace{0.05cm}.$$ | ||
| + | *Since this does not change the memory allocation, all further binary values generated will also be $1$ each ⇒ $\underline{P = 1}$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(5)''' <u>Answer 1</u> is correct: | ||
| + | *One speaks of an M-sequence only if $P = 2^G –1$ holds. | ||
| + | *Here, "M" stands for "maximum". | ||
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Modulation Methods: Exercises|^5.3 Spread Sequences for CDMA^]] |
Latest revision as of 17:32, 20 December 2021
The diagram shows two possible generators for generating PN sequences in unipolar representation: $u_ν ∈ \{0, 1\}$.
- The upper generator with the coefficients
- $$ g_0 = 1 \hspace{0.05cm}, \hspace{0.2cm}g_1 = 0 \hspace{0.05cm}, \hspace{0.2cm}g_2 = 1 \hspace{0.05cm}, \hspace{0.2cm}g_3 = 1 \hspace{0.05cm}$$
- is denoted by the octal identifier $(g_3,\ g_2,\ g_1,\ g_0)_{\rm octal} = (15)$.
- Accordingly, the octal identifier of the second PN generator is $(17)$.
- One speaks of an M-sequence if for the period length of the sequence $〈u_ν〉$ holds:
- $$P = 2^G – 1.$$
- Here, $G$ denotes the degree of the shift register, which is equal to the number of memory cells.
Notes:
- The exercise belongs to the chapter Spreading Sequences for CDMA.
- Reference is also made to the chapter Generation of Discrete Random Variables in the book "Theory of Stochastic Signals".
- We would also like to draw your attention to the (German language) learning video
Erläuterung der PN–Generatoren an einem Beispiel ⇒ "Explanation of PN generators using an example".
Questions
Solution
(1) The degree $\underline{G = 3}$ is equal to the number of memory cells of the shift register.
(2) From the given sequence the period length $\underline{P = 7}$ can be read. Because of $P = 2^G –1$ it is an M-sequence.
(3) Solutions 2, 3 and 4 are correct:
- The maximum number of consecutive "ones" is $G$ (whenever there is a "one" in all $G$ memory cells).
- On the other hand, it is not possible that all memory cells are filled with zeros (otherwise only zeros would be generated).
- Therefore, there is always one more "ones" than zeros.
- The period length of the sequence "$1 0 1 0 1 0$ ..." is $P = 2$. For an M-sequence $P = 2^G –1$. For no value of $G$: $P = 2$ is possible.
(4) If all memory cells are occupied with ones, the generator with the octal identifier $(17)$ returns a $1$ again:
- $$u_{\nu} \big [ u_{\nu-1} + u_{\nu-2} + u_{\nu-3} \big ] \,\,{\rm mod} \,\,2 =1 \hspace{0.05cm}.$$
- Since this does not change the memory allocation, all further binary values generated will also be $1$ each ⇒ $\underline{P = 1}$.
(5) Answer 1 is correct:
- One speaks of an M-sequence only if $P = 2^G –1$ holds.
- Here, "M" stands for "maximum".