Difference between revisions of "Signal Representation/Discrete Fourier Transform (DFT)"
| (74 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Time and Frequency-Discrete Signal Representation |
| − | |Vorherige Seite= | + | |Vorherige Seite=Discrete-Time Signal Representation |
| − | |Nächste Seite= | + | |Nächste Seite=Possible Errors When Using DFT |
}} | }} | ||
| − | == | + | ==Arguments for the discrete implementation of the Fourier transform== |
| + | <br> | ||
| + | The »'''Fourier transform'''« according to the previous description in chapter [[Signal_Representation/The_Fourier_Transform_and_its_Inverse#The_first_Fourier_integral|»Aperiodic Signals – Pulses«]] has an infinitely high selectivity due to the unlimited extension of the integration interval and is therefore an ideal theoretical tool of spectral analysis. | ||
| − | + | If the spectral components $X(f)$ of a time function $x(t)$ are to be determined numerically, the general transformation equations | |
| − | |||
| − | $$\begin{align*}X(f) & = \int_{-\infty | + | :$$\begin{align*}X(f) & = \int_{-\infty |
| − | }^{+\infty}x(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi f t}\hspace{0.1cm} {\rm d}t\hspace{0.5cm} \Rightarrow\hspace{0.5cm} {\ | + | }^{+\infty}x(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi f t}\hspace{0.1cm} {\rm d}t\hspace{0.5cm} \Rightarrow\hspace{0.5cm} \text{Transform}\hspace{0.7cm} \Rightarrow\hspace{0.5cm} \text{first Fourier integral} |
\hspace{0.05cm},\\ | \hspace{0.05cm},\\ | ||
x(t) & = \int_{-\infty | x(t) & = \int_{-\infty | ||
}^{+\infty}\hspace{-0.15cm}X(f) \cdot {\rm e}^{\hspace{0.05cm}+{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi f t}\hspace{0.1cm} {\rm d}f\hspace{0.35cm} \Rightarrow\hspace{0.5cm} | }^{+\infty}\hspace{-0.15cm}X(f) \cdot {\rm e}^{\hspace{0.05cm}+{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi f t}\hspace{0.1cm} {\rm d}f\hspace{0.35cm} \Rightarrow\hspace{0.5cm} | ||
| − | {\ | + | \text{Inverse Transform}\hspace{0.4cm} \Rightarrow\hspace{0.5cm} \text{second Fourier integral} |
\hspace{0.05cm}\end{align*}$$ | \hspace{0.05cm}\end{align*}$$ | ||
| − | + | are unsuitable for two reasons: | |
| − | + | #The equations apply exclusively to continuous-time signals. With digital computers or signal processors, however, one can only process discrete-time signals. | |
| − | + | #For a numerical evaluation of the two Fourier integrals it is necessary to limit the respective integration interval to a finite value. | |
| − | + | {{BlaueBox|TEXT= | |
| − | + | $\text{This leads to the following consequence:}$ | |
| − | |||
| + | A »'''continuous-valued signal'''« must undergo two processes before the numerical determination of its spectral properties, viz. | ||
| + | #that of »'''sampling'''« for discretization, and<br> | ||
| + | #that of »'''windowing'''« to limit the integration interval.}} | ||
| − | |||
| + | In the following, starting from an aperiodic time function $x(t)$ and the corresponding Fourier spectrum $X(f)$ a time and frequency-discrete description suitable for computer processing is developed step by step. | ||
| − | |||
| − | |||
| − | + | ==Time discretization – Periodification in the frequency domain== | |
| + | <br> | ||
| + | The following graphs show uniformly the time domain on the left and the frequency domain on the right. | ||
| + | *Without limiting generality, $x(t)$ and $X(f)$ are each real and Gaussian. | ||
| − | + | *According to the chapter [[Signal_Representation/Time_Discrete_Signal_Representation|»Discrete-Time Signal Representation«]] one can describe the sampling of the time signal $x(t)$ by multiplying it by a Dirac delta train ⇒ <br>»Dirac comb in the time domain« | |
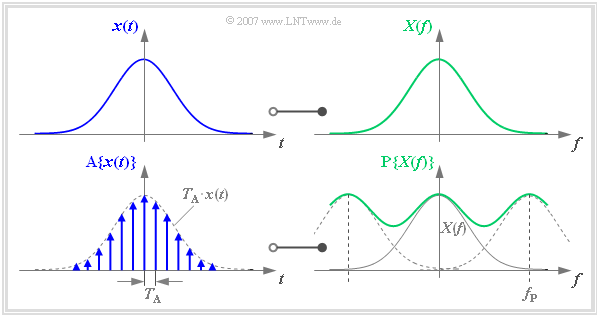
| + | [[File:P_ID1132__Sig_T_5_1_S2_neu.png|right|frame| Time discretization ⇒ Periodification in the frequency domain. <u>Notation:</u><br> ${\rm A}\{x(t)\}$: Signal $x(t)$ after »sampling« $($German: "Abtastung"$)$ ⇒ $\rm A\{\text{...}\}$ <br> ${\rm P}\{X(f)\}$: Spectrum $X(f)$ after »periodification« ⇒ $\rm P\{\text{...}\}$]] | ||
| + | |||
| + | :$$p_{\delta}(t) = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot | ||
| + | \delta (t- \nu \cdot T_{\rm A} | ||
| + | )\hspace{0.05cm}.$$ | ||
| + | |||
| + | The result is the time signal sampled at a distance $T_{\rm A}$: | ||
| − | $${\rm A}\{x(t)\} = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot x(\nu \cdot T_{\rm A})\cdot | + | :$${\rm A}\{x(t)\} = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot x(\nu \cdot T_{\rm A})\cdot |
\delta (t- \nu \cdot T_{\rm A} | \delta (t- \nu \cdot T_{\rm A} | ||
)\hspace{0.05cm}.$$ | )\hspace{0.05cm}.$$ | ||
| − | + | We transform this sampled signal $\text{A}\{ x(t)\}$ into the frequency domain: | |
| + | *The multiplication of the Dirac comb $p_{\delta}(t)$ with $x(t)$ corresponds in the frequency domain to the convolution of $P_{\delta}(f)$ with $X(f)$. | ||
| + | |||
| + | *The result is the periodified spectrum $\text{P}\{ X(f)\}$, where $f_{\rm | ||
| + | P}$ indicates the frequency period of the function $\text{P}\{ X(f)\}$ : | ||
| − | $${\rm A}\{x(t)\} \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} {\rm P}\{X(f)\} = \sum_{\mu = - \infty }^{+\infty} | + | :$${\rm A}\{x(t)\} \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} {\rm P}\{X(f)\} = \sum_{\mu = - \infty }^{+\infty} |
| − | X (f- \mu \cdot f_{\rm P} )\ | + | X (f- \mu \cdot f_{\rm P} ).$$ |
| − | + | ||
| + | This relation was already derived in the chapter [[Signal_Representation/Time_Discrete_Signal_Representation|"Discrete-Time Signal Representation"]] but with slightly different nomenclature: | ||
| + | *We now denote the sampled signal by $\text{A}\{ x(t)\}$ instead of $x_{\rm A}(t)$. | ||
| − | + | * The »frequency period« is now denoted by $f_{\rm P} = 1/T_{\rm A}$ instead of $f_{\rm A} = 1/T_{\rm A}$. | |
| − | * | ||
| − | |||
| − | + | These nomenclature changes are justified in the following sections. | |
| − | |||
| − | |||
| − | |||
| + | The graph above shows the functional relationship described here. It should be noted: | ||
| + | #The frequency period $f_{\rm P}$ has been deliberately chosen to be small here so that the overlap of the spectra to be summed can be clearly seen. | ||
| + | #In practice $f_{\rm P}$ should be at least twice as large as the largest frequency contained in the signal $x(t)$ due to the sampling theorem. | ||
| + | #If this is not fulfilled, then »'''aliasing'''« must be expected - see chapter [[Signal_Representation/Possible_Errors_When_Using_DFT|»Possible Errors when using DFT«]]. | ||
| − | |||
| − | + | ==Frequency discretization – Periodification in the time domain == | |
| − | + | <br> | |
| − | $${\rm A}\{X(f)\} = X(f) \cdot \sum_{\mu = - \infty }^{+\infty} | + | The discretization of $X(f)$ can also be described by a multiplication with a Dirac comb in the frequency domain. The result is the sampled spectrum with distance $f_{\rm A}$: |
| + | :$${\rm A}\{X(f)\} = X(f) \cdot \sum_{\mu = - \infty }^{+\infty} | ||
f_{\rm A} \cdot \delta (f- \mu \cdot f_{\rm A } ) = \sum_{\mu = - \infty }^{+\infty} | f_{\rm A} \cdot \delta (f- \mu \cdot f_{\rm A } ) = \sum_{\mu = - \infty }^{+\infty} | ||
f_{\rm A} \cdot X(\mu \cdot f_{\rm A } ) \cdot\delta (f- \mu \cdot f_{\rm A } )\hspace{0.05cm}.$$ | f_{\rm A} \cdot X(\mu \cdot f_{\rm A } ) \cdot\delta (f- \mu \cdot f_{\rm A } )\hspace{0.05cm}.$$ | ||
| − | + | *If one transforms the Dirac comb $($with impulse weights $f_{\rm A})$ into the time domain, one obtains with $T_{\rm P} = 1/f_{\rm A}$: | |
| − | $$\sum_{\mu = - \infty }^{+\infty} | + | :$$\sum_{\mu = - \infty }^{+\infty} |
f_{\rm A} \cdot \delta (f- \mu \cdot f_{\rm A } ) \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} | f_{\rm A} \cdot \delta (f- \mu \cdot f_{\rm A } ) \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} | ||
\sum_{\nu = - \infty }^{+\infty} | \sum_{\nu = - \infty }^{+\infty} | ||
\delta (t- \nu \cdot T_{\rm P } ) \hspace{0.05cm}.$$ | \delta (t- \nu \cdot T_{\rm P } ) \hspace{0.05cm}.$$ | ||
| − | + | *The multiplication with $X(f)$ corresponds in the time domain to the convolution with $x(t)$. One obtains the signal $\text{P}\{ x(t)\}$ periodified with distance $T_{\rm P}$: | |
| − | $${\rm A}\{X(f)\} \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} | + | :$${\rm A}\{X(f)\} \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} |
{\rm P}\{x(t)\} = x(t) \star \sum_{\nu = - \infty }^{+\infty} | {\rm P}\{x(t)\} = x(t) \star \sum_{\nu = - \infty }^{+\infty} | ||
\delta (t- \nu \cdot T_{\rm P } )= \sum_{\nu = - \infty }^{+\infty} | \delta (t- \nu \cdot T_{\rm P } )= \sum_{\nu = - \infty }^{+\infty} | ||
x (t- \nu \cdot T_{\rm P } ) \hspace{0.05cm}.$$ | x (t- \nu \cdot T_{\rm P } ) \hspace{0.05cm}.$$ | ||
| − | [[File:P_ID1134__Sig_T_5_1_S3_neu.png| | + | |
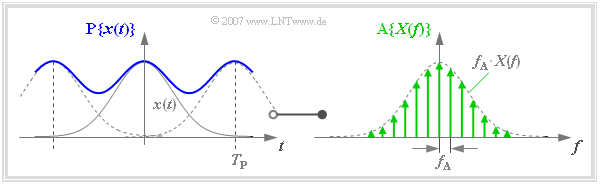
| − | + | {{GraueBox|TEXT= | |
| + | [[File:P_ID1134__Sig_T_5_1_S3_neu.png|right|frame|Frequency discretization – Periodization in the time domain]] | ||
| + | $\text{Example 1:}$ | ||
| + | This correlation is illustrated in the graph: | ||
| + | *Due to the coarse frequency rastering, this example results in a relatively small value for the time period $T_{\rm P}$ . | ||
| − | + | * Therefore due to overlaps, the $($blue$)$ periodified time signal $\text{P}\{ x(t)\}$ differs significantly from $x(t)$. | |
| − | |||
| − | + | *If one wants to achieve $\text{P}\{ x(t)\} \approx x(t)$ then $T_{\rm P}$ must be chosen much larger than in this example.}} | |
| − | + | ==Finite signal representation== | |
| − | + | <br> | |
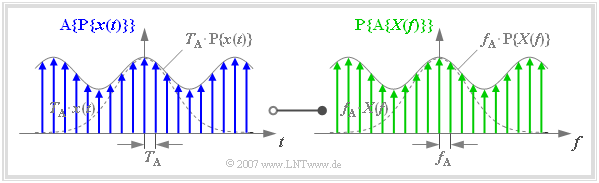
| − | * | + | [[File:P_ID1135__Sig_T_5_1_S4_neu.png|right|frame|Finite signals of the Discrete Fourier Transform $\rm (DFT)$]] |
| + | One arrives at the so-called »finite signal representation«, if both | ||
| + | *the time function $x(t)$, | ||
| − | $ | + | *the spectral function $X(f)$ |
| − | * | + | |
| − | + | are specified exclusively by their sample values. This graph is to be interpreted as follows: | |
| + | *In the left graph, the function $\text{A}\{ \text{P}\{ x(t)\}\}$ is drawn in blue. This results from sampling the periodified time function $\text{P}\{ x(t)\}$ with equidistant Dirac deltas with distance $T_{\rm A} = 1/f_{\rm P}$. | ||
| + | |||
| + | *In the right graph, the function $\text{P}\{ \text{A}\{ X(f)\}\}$ is drawn in green. This results from the periodification $($with $f_{\rm P})$ of the sampled spectral function $\{ \text{A}\{ X(f)\}\}$. | ||
| + | |||
| + | *There is a Fourier correspondence between the blue finite signal $($in the left sketch$)$ and the green finite signal $($in the right sketch$)$, as follows: | ||
| − | $$f_{\rm P} = N \cdot f_{\rm A} \hspace{0.5cm} \Rightarrow\hspace{0.5cm} {1}/{T_{\rm A}}= N \cdot f_{\rm A} \hspace{0.5cm} \Rightarrow\hspace{0.5cm} | + | :$${\rm A}\{{\rm P}\{x(t)\}\} \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} {\rm P}\{{\rm A}\{X(f)\}\} \hspace{0.05cm}.$$ |
| + | |||
| + | *The Dirac delta lines of the periodic continuation $\text{P}\{ \text{A}\{ X(f)\}\}$ of the sampled spectral function, however, only fall into the same frequency grid as those of $\text{A}\{ X(f)\}$ if the frequency period $f_{\rm P}$ is an integer multiple $(N)$ of the frequency sampling interval $f_{\rm A}$. | ||
| + | |||
| + | *Therefore, when using the finite signal representation, the following condition must always be fulfilled, where in practice the natural number $N$ is usually a power of two $($the above graph is based on the value $N = 8)$: | ||
| + | |||
| + | :$$f_{\rm P} = N \cdot f_{\rm A} \hspace{0.5cm} \Rightarrow\hspace{0.5cm} {1}/{T_{\rm A}}= N \cdot f_{\rm A} \hspace{0.5cm} \Rightarrow\hspace{0.5cm} | ||
N \cdot f_{\rm A}\cdot T_{\rm A} = 1\hspace{0.05cm}.$$ | N \cdot f_{\rm A}\cdot T_{\rm A} = 1\hspace{0.05cm}.$$ | ||
| − | + | *If the condition $N \cdot f_{\rm A} \cdot T_{\rm A} = 1$ is fulfilled then the order of periodization and sampling is interchangeable. Thus: | |
| − | |||
| − | $${\rm A}\{{\rm P}\{x(t)\}\} = {\rm P}\{{\rm A}\{x(t)\}\}\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} | + | :$${\rm A}\{{\rm P}\{x(t)\}\} = {\rm P}\{{\rm A}\{x(t)\}\}\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} |
{\rm P}\{{\rm A}\{X(f)\}\} = {\rm A}\{{\rm P}\{X(f)\}\}\hspace{0.05cm}.$$ | {\rm P}\{{\rm A}\{X(f)\}\} = {\rm A}\{{\rm P}\{X(f)\}\}\hspace{0.05cm}.$$ | ||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Conclusions:}$ | ||
| + | #The time function $\text{P}\{ \text{A}\{ x(t)\}\}$ has the period $T_{\rm P} = N \cdot T_{\rm A}$. | ||
| + | #The period in the frequency domain is $f_{\rm P} = N \cdot f_{\rm A}$. | ||
| + | #For the description of the discretized time and frequency response in each case $N$ '''complex numerical values''' in the form of impulse weights are sufficient.}} | ||
| − | |||
| − | |||
| − | {{ | + | {{GraueBox|TEXT= |
| + | $\text{Example 2:}$ | ||
| + | A time-limited $($pulse-like$)$ signal $x(t)$ is present in sampled form, where the distance between two samples is $T_{\rm A} = 1\, {\rm µ s}$: | ||
| + | *After a discrete Fourier transform with $N = 512$ the spectrum $X(f)$ is available in form of frequency-samples at spacing $f_{\rm A} = (N \cdot T_{\rm A})^{-1} \approx 1.953\,\text{kHz} $. | ||
| + | *Increasing the DFT parameter to $N= 2048$ results in a $($four times$)$ finer frequency grid with $f_{\rm A} \approx 488\,\text{Hz}$.}} | ||
| − | |||
| − | + | ==From the continuous to the discrete Fourier transform== | |
| + | <br> | ||
| + | From the conventional [[Signal_Representation/Fourier_Transform_and_its_Inverse#The_first_Fourier_integral|»first Fourier integral«]] | ||
| − | $$X(f) =\int_{-\infty | + | :$$X(f) =\int_{-\infty |
| − | }^{+\infty}x(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi f \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}t$$ | + | }^{+\infty}x(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}t$$ |
| − | + | arises from discretization $(\text{d}t \to T_{\rm A}$, $t \to \nu \cdot T_{\rm A}$, $f \to \mu \cdot f_{\rm A}$, $T_{\rm A} \cdot f_{\rm A} = 1/N)$ the sampled and periodified spectral function | |
| − | $${\rm P}\{X(\mu \cdot f_{\rm A})\} = T_{\rm A} \cdot \sum_{\nu = 0 }^{N-1} | + | :$${\rm P}\{X(\mu \cdot f_{\rm A})\} = T_{\rm A} \cdot \sum_{\nu = 0 }^{N-1} |
{\rm P}\{x(\nu \cdot T_{\rm A})\}\cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm} \cdot \hspace{0.05cm}\nu \hspace{0.05cm} | {\rm P}\{x(\nu \cdot T_{\rm A})\}\cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm} \cdot \hspace{0.05cm}\nu \hspace{0.05cm} | ||
\cdot \hspace{0.05cm}\mu /N} \hspace{0.05cm}.$$ | \cdot \hspace{0.05cm}\mu /N} \hspace{0.05cm}.$$ | ||
| − | + | It is taken into account that due to the discretization, the periodified functions are to be used in each case. | |
| − | * | + | |
| − | $$d(\nu) = | + | For reasons of simplified notation, we now make the following substitutions: |
| + | *The $N$ »time-domain coefficients« are with the variable $\nu = 0$, ... , $N - 1$: | ||
| + | :$$d(\nu) = | ||
{\rm P}\left\{x(t)\right\}{\big|}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A}}\hspace{0.05cm}.$$ | {\rm P}\left\{x(t)\right\}{\big|}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A}}\hspace{0.05cm}.$$ | ||
| − | * | + | *Let $N$ »frequency domain coefficients« be associated with the variable $\mu = 0,$ ... , $N-1$: |
| − | $$D(\mu) = f_{\rm A} \cdot | + | :$$D(\mu) = f_{\rm A} \cdot |
{\rm P}\left\{X(f)\right\}{\big|}_{f \hspace{0.05cm}= \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm A}}\hspace{0.05cm}.$$ | {\rm P}\left\{X(f)\right\}{\big|}_{f \hspace{0.05cm}= \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm A}}\hspace{0.05cm}.$$ | ||
| − | * | + | *Abbreviation is written for the from $N$ dependent »complex rotation factor« : |
| − | $$w | + | :$$w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} |
| − | = \cos \left( | + | = \cos \left( {2 \pi}/{N}\right)-{\rm j} \cdot \sin \left( {2 \pi}/{N}\right) |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Definition:}$ | ||
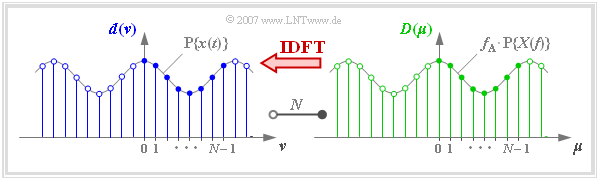
| + | The term »Discrete Fourier Transform« $\rm (DFT)$ means the calculation of the $N$ spectral coefficients $D(\mu)$ from the $N$ signal coefficients $d(\nu)$: | ||
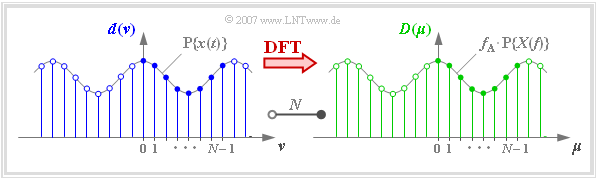
| + | [[File:P_ID2730__Sig_T_5_1_S5_neu.png|right|frame|On defining the »Discrete Fourier Transform« $\rm (DFT)$ with $N=8$]] | ||
| + | :$$D(\mu) = \frac{1}{N} \cdot \sum_{\nu = 0 }^{N-1} | ||
| + | d(\nu)\cdot {w}^{\hspace{0.05cm}\nu \hspace{0.07cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}. $$ | ||
| + | : | ||
| + | In the diagram you can see: | ||
| + | *The $N = 8$ signal coefficients $d(\nu)$ by the blue filling, | ||
| − | + | *the $N = 8$ spectral coefficients $D(\mu)$ at the green filling.}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==Inverse discrete Fourier transform== | |
| + | <br> | ||
| + | The »inverse discrete Fourier transform« describes the [[Signal_Representation/Fourier_Transform_and_its_Inverse#The_second_Fourier_integral|»second Fourier integral«]]: | ||
| − | $$\begin{align*}x(t) & = \int_{-\infty | + | :$$\begin{align*}x(t) & = \int_{-\infty |
| − | }^{+\infty}X(f) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi f \hspace{0.05cm} | + | }^{+\infty}X(f) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm} |
t}\hspace{0.1cm} {\rm d}f\end{align*}$$ | t}\hspace{0.1cm} {\rm d}f\end{align*}$$ | ||
| − | in | + | in discretized form: |
| − | + | :$$d(\nu) = | |
| − | $$d(\nu) = | ||
{\rm P}\left\{x(t)\right\}{\big|}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm | {\rm P}\left\{x(t)\right\}{\big|}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm | ||
| − | A}}\hspace{0. | + | A}}\hspace{0.01cm}.$$ |
| − | |||
| − | {{Definition} | + | {{BlaueBox|TEXT= $\text{Definition:}$ The term »Inverse Discrete Fourier Transform» $\rm (IDFT)$ means the calculation of the signal coefficients $d(\nu)$ from the spectral coefficients $D(\mu)$: |
| − | + | [[File:P_ID2731__Sig_T_5_1_S6_neu.png|right|frame|On defining the »Inverse Discrete Fourier Transform« $\rm (IDFT)$ with $N=8$]] | |
| + | :$$d(\nu) = \sum_{\mu = 0 }^{N-1} | ||
| + | D(\mu) \cdot {w}^{-\nu \hspace{0.07cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$ | ||
| + | |||
| + | *With indices $\nu = 0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, N-1, $ and $\mu = 0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, N-1$ holds: | ||
| + | :$$d(\nu) = | ||
| + | {\rm P}\left\{x(t)\right\}{\big \vert}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm | ||
| + | A} }\hspace{0.01cm},$$ | ||
| − | $$ | + | :$$D(\mu) = f_{\rm A} \cdot |
| − | + | {\rm P}\left\{X(f)\right\}{\big \vert}_{f \hspace{0.05cm}= \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm A} } | |
| − | + | \hspace{0.01cm},$$ | |
| + | :$$w = {\rm e}^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} | ||
| + | \hspace{0.01cm}.$$ | ||
| − | [[ | + | *A comparison between [[Signal_Representation/Discrete_Fourier_Transform_(DFT)#From_the_continuous_to_the_discrete_Fourier_transform|»DFT«]] and »IDFT« shows that exactly the same algorithm can be used. |
| − | In | + | *The only differences between IDFT and DFT are: |
| + | #The exponent of the rotation factor is to be applied with different sign. | ||
| + | #In the IDFT, the division by $N$ is omitted.}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==Interpretation of DFT and IDFT== | |
| − | + | <br> | |
| − | + | The graph shows the discrete coefficients in the time and frequency domain together with the periodified continuous-time functions. | |
| − | |||
| − | |||
| − | |||
| + | [[File:P_ID1136__Sig_T_5_1_S7_neu.png|right|frame|Time and frequency coefficients of the DFT]] | ||
| − | + | When using DFT or IDFT, please note: | |
| + | #According to the above definitions, the DFT coefficients $d(ν)$ and $D(\mu)$ always have the unit of the time function. | ||
| + | #Dividing $D(\mu)$ by $f_{\rm A}$, one obtains the spectral value $X(\mu \cdot f_{\rm A})$. | ||
| + | #The spectral coefficients $D(\mu)$ must always be complex in order to be able to consider odd time functions. | ||
| + | #One also uses complex time coefficients $d(\nu)$ ⇒ DFT and IDFT are also applicable to band-pass signals. | ||
| + | #The basic interval for $\nu$ and $\mu$ is usually defined as the range from $0$ to $N - 1$ $($filled circles in the graph$)$. | ||
| + | <br clear=all> | ||
| + | With the complex-valued number sequences | ||
| + | :$$\langle \hspace{0.03cm}d(\nu)\hspace{0.03cm}\rangle = \langle \hspace{0.03cm}d(0), \hspace{0.05cm}\text{...} \hspace{0.05cm} , d(N-1) \hspace{0.03cm}\rangle,$$ | ||
| + | :$$\langle \hspace{0.03cm}D(\mu)\hspace{0.03cm}\rangle = \langle \hspace{0.03cm}D(0), \hspace{0.05cm}\text{...} \hspace{0.05cm} , D(N-1) \hspace{0.03cm}\rangle,$$ | ||
| − | + | DFT and IDFT are symbolized similarly to the conventional Fourier transform: | |
| + | :$$\langle \hspace{0.03cm} D(\mu)\hspace{0.03cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.03cm} d(\nu) \hspace{0.03cm}\rangle \hspace{0.05cm}.$$ | ||
| + | #If the function $x(t)$ is already limited to the range $0 \le t \lt N \cdot T_{\rm A}$ then the IDFT output directly give the samples of the time function: $d(\nu) = x(\nu \cdot T_{\rm A}).$ | ||
| + | #If $x(t)$ is shifted with respect to the basic interval, one has to choose the association shown in $\text{Example 3}$ between $x(t)$ and the coefficients $d(\nu)$. | ||
| − | |||
| − | + | {{GraueBox|TEXT= | |
| − | + | $\text{Example 3:}$ | |
| − | + | The upper graph shows the asymmetric triangular pulse $x(t)$ whose absolute width is smaller than $T_{\rm P} = N \cdot T_{\rm A}$. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | [[File:EN_Sig_T_5_1_S7b_neu.png|right|frame|On assigning of the DFT coefficients with $N=8$]] | ||
| − | |||
| − | + | The sketch below shows the assigned DFT coefficients $($valid for $N = 8)$. | |
| − | + | *For $\nu = 0,\hspace{0.05cm}\text{...} \hspace{0.05cm} , N/2 = 4$ holds $d(\nu) = x(\nu \cdot T_{\rm A})$ : | |
| − | + | :$$d(0) = x (0)\hspace{0.05cm}, \hspace{0.15cm} | |
| + | d(1) = x (T_{\rm A})\hspace{0.05cm}, \hspace{0.15cm} | ||
| + | d(2) = x (2T_{\rm A})\hspace{0.05cm}, $$ | ||
| + | :$$d(3) = x (3T_{\rm A})\hspace{0.05cm}, \hspace{0.15cm} | ||
| + | d(4) = x (4T_{\rm A})\hspace{0.05cm}.$$ | ||
| + | *The coefficients $d(5)$, $d(6)$ and d$(7)$ are to be set as follows: | ||
| − | + | :$$d(5) = x (-3T_{\rm A})\hspace{0.05cm}, \hspace{0.35cm} | |
| − | + | d(6) = x (-2T_{\rm A})\hspace{0.05cm}, \hspace{0.35cm} | |
| − | + | d(7) = x (-T_{\rm A})\hspace{0.05cm}$$ | |
| − | + | :$$ \Rightarrow \hspace{0.2cm}d(\nu) = x \big ((\nu\hspace{-0.05cm} - \hspace{-0.05cm} N ) \cdot T_{\rm A}\big ). $$ | |
| − | {{ | ||
| − | + | }} | |
| − | [[Aufgaben:5.2 Inverse | + | ==Exercises for the chapter== |
| + | <br> | ||
| + | [[Aufgaben:Exercise 5.2: Inverse Discrete Fourier Transform|Exercise 5.2: Inverse Discrete Fourier Transform]] | ||
| − | [[Aufgaben:5.2Z DFT | + | [[Aufgaben:Exercise 5.2Z: DFT of a Triangular Pulse|Exercise 5.2Z: DFT of a Triangular Pulse]] |
{{Display}} | {{Display}} | ||
Latest revision as of 16:57, 28 June 2023
Contents
- 1 Arguments for the discrete implementation of the Fourier transform
- 2 Time discretization – Periodification in the frequency domain
- 3 Frequency discretization – Periodification in the time domain
- 4 Finite signal representation
- 5 From the continuous to the discrete Fourier transform
- 6 Inverse discrete Fourier transform
- 7 Interpretation of DFT and IDFT
- 8 Exercises for the chapter
Arguments for the discrete implementation of the Fourier transform
The »Fourier transform« according to the previous description in chapter »Aperiodic Signals – Pulses« has an infinitely high selectivity due to the unlimited extension of the integration interval and is therefore an ideal theoretical tool of spectral analysis.
If the spectral components $X(f)$ of a time function $x(t)$ are to be determined numerically, the general transformation equations
- $$\begin{align*}X(f) & = \int_{-\infty }^{+\infty}x(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi f t}\hspace{0.1cm} {\rm d}t\hspace{0.5cm} \Rightarrow\hspace{0.5cm} \text{Transform}\hspace{0.7cm} \Rightarrow\hspace{0.5cm} \text{first Fourier integral} \hspace{0.05cm},\\ x(t) & = \int_{-\infty }^{+\infty}\hspace{-0.15cm}X(f) \cdot {\rm e}^{\hspace{0.05cm}+{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi f t}\hspace{0.1cm} {\rm d}f\hspace{0.35cm} \Rightarrow\hspace{0.5cm} \text{Inverse Transform}\hspace{0.4cm} \Rightarrow\hspace{0.5cm} \text{second Fourier integral} \hspace{0.05cm}\end{align*}$$
are unsuitable for two reasons:
- The equations apply exclusively to continuous-time signals. With digital computers or signal processors, however, one can only process discrete-time signals.
- For a numerical evaluation of the two Fourier integrals it is necessary to limit the respective integration interval to a finite value.
$\text{This leads to the following consequence:}$
A »continuous-valued signal« must undergo two processes before the numerical determination of its spectral properties, viz.
- that of »sampling« for discretization, and
- that of »windowing« to limit the integration interval.
In the following, starting from an aperiodic time function $x(t)$ and the corresponding Fourier spectrum $X(f)$ a time and frequency-discrete description suitable for computer processing is developed step by step.
Time discretization – Periodification in the frequency domain
The following graphs show uniformly the time domain on the left and the frequency domain on the right.
- Without limiting generality, $x(t)$ and $X(f)$ are each real and Gaussian.
- According to the chapter »Discrete-Time Signal Representation« one can describe the sampling of the time signal $x(t)$ by multiplying it by a Dirac delta train ⇒
»Dirac comb in the time domain«
- $$p_{\delta}(t) = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot \delta (t- \nu \cdot T_{\rm A} )\hspace{0.05cm}.$$
The result is the time signal sampled at a distance $T_{\rm A}$:
- $${\rm A}\{x(t)\} = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot x(\nu \cdot T_{\rm A})\cdot \delta (t- \nu \cdot T_{\rm A} )\hspace{0.05cm}.$$
We transform this sampled signal $\text{A}\{ x(t)\}$ into the frequency domain:
- The multiplication of the Dirac comb $p_{\delta}(t)$ with $x(t)$ corresponds in the frequency domain to the convolution of $P_{\delta}(f)$ with $X(f)$.
- The result is the periodified spectrum $\text{P}\{ X(f)\}$, where $f_{\rm P}$ indicates the frequency period of the function $\text{P}\{ X(f)\}$ :
- $${\rm A}\{x(t)\} \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} {\rm P}\{X(f)\} = \sum_{\mu = - \infty }^{+\infty} X (f- \mu \cdot f_{\rm P} ).$$
This relation was already derived in the chapter "Discrete-Time Signal Representation" but with slightly different nomenclature:
- We now denote the sampled signal by $\text{A}\{ x(t)\}$ instead of $x_{\rm A}(t)$.
- The »frequency period« is now denoted by $f_{\rm P} = 1/T_{\rm A}$ instead of $f_{\rm A} = 1/T_{\rm A}$.
These nomenclature changes are justified in the following sections.
The graph above shows the functional relationship described here. It should be noted:
- The frequency period $f_{\rm P}$ has been deliberately chosen to be small here so that the overlap of the spectra to be summed can be clearly seen.
- In practice $f_{\rm P}$ should be at least twice as large as the largest frequency contained in the signal $x(t)$ due to the sampling theorem.
- If this is not fulfilled, then »aliasing« must be expected - see chapter »Possible Errors when using DFT«.
Frequency discretization – Periodification in the time domain
The discretization of $X(f)$ can also be described by a multiplication with a Dirac comb in the frequency domain. The result is the sampled spectrum with distance $f_{\rm A}$:
- $${\rm A}\{X(f)\} = X(f) \cdot \sum_{\mu = - \infty }^{+\infty} f_{\rm A} \cdot \delta (f- \mu \cdot f_{\rm A } ) = \sum_{\mu = - \infty }^{+\infty} f_{\rm A} \cdot X(\mu \cdot f_{\rm A } ) \cdot\delta (f- \mu \cdot f_{\rm A } )\hspace{0.05cm}.$$
- If one transforms the Dirac comb $($with impulse weights $f_{\rm A})$ into the time domain, one obtains with $T_{\rm P} = 1/f_{\rm A}$:
- $$\sum_{\mu = - \infty }^{+\infty} f_{\rm A} \cdot \delta (f- \mu \cdot f_{\rm A } ) \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} \sum_{\nu = - \infty }^{+\infty} \delta (t- \nu \cdot T_{\rm P } ) \hspace{0.05cm}.$$
- The multiplication with $X(f)$ corresponds in the time domain to the convolution with $x(t)$. One obtains the signal $\text{P}\{ x(t)\}$ periodified with distance $T_{\rm P}$:
- $${\rm A}\{X(f)\} \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} {\rm P}\{x(t)\} = x(t) \star \sum_{\nu = - \infty }^{+\infty} \delta (t- \nu \cdot T_{\rm P } )= \sum_{\nu = - \infty }^{+\infty} x (t- \nu \cdot T_{\rm P } ) \hspace{0.05cm}.$$
$\text{Example 1:}$ This correlation is illustrated in the graph:
- Due to the coarse frequency rastering, this example results in a relatively small value for the time period $T_{\rm P}$ .
- Therefore due to overlaps, the $($blue$)$ periodified time signal $\text{P}\{ x(t)\}$ differs significantly from $x(t)$.
- If one wants to achieve $\text{P}\{ x(t)\} \approx x(t)$ then $T_{\rm P}$ must be chosen much larger than in this example.
Finite signal representation
One arrives at the so-called »finite signal representation«, if both
- the time function $x(t)$,
- the spectral function $X(f)$
are specified exclusively by their sample values. This graph is to be interpreted as follows:
- In the left graph, the function $\text{A}\{ \text{P}\{ x(t)\}\}$ is drawn in blue. This results from sampling the periodified time function $\text{P}\{ x(t)\}$ with equidistant Dirac deltas with distance $T_{\rm A} = 1/f_{\rm P}$.
- In the right graph, the function $\text{P}\{ \text{A}\{ X(f)\}\}$ is drawn in green. This results from the periodification $($with $f_{\rm P})$ of the sampled spectral function $\{ \text{A}\{ X(f)\}\}$.
- There is a Fourier correspondence between the blue finite signal $($in the left sketch$)$ and the green finite signal $($in the right sketch$)$, as follows:
- $${\rm A}\{{\rm P}\{x(t)\}\} \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} {\rm P}\{{\rm A}\{X(f)\}\} \hspace{0.05cm}.$$
- The Dirac delta lines of the periodic continuation $\text{P}\{ \text{A}\{ X(f)\}\}$ of the sampled spectral function, however, only fall into the same frequency grid as those of $\text{A}\{ X(f)\}$ if the frequency period $f_{\rm P}$ is an integer multiple $(N)$ of the frequency sampling interval $f_{\rm A}$.
- Therefore, when using the finite signal representation, the following condition must always be fulfilled, where in practice the natural number $N$ is usually a power of two $($the above graph is based on the value $N = 8)$:
- $$f_{\rm P} = N \cdot f_{\rm A} \hspace{0.5cm} \Rightarrow\hspace{0.5cm} {1}/{T_{\rm A}}= N \cdot f_{\rm A} \hspace{0.5cm} \Rightarrow\hspace{0.5cm} N \cdot f_{\rm A}\cdot T_{\rm A} = 1\hspace{0.05cm}.$$
- If the condition $N \cdot f_{\rm A} \cdot T_{\rm A} = 1$ is fulfilled then the order of periodization and sampling is interchangeable. Thus:
- $${\rm A}\{{\rm P}\{x(t)\}\} = {\rm P}\{{\rm A}\{x(t)\}\}\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} {\rm P}\{{\rm A}\{X(f)\}\} = {\rm A}\{{\rm P}\{X(f)\}\}\hspace{0.05cm}.$$
$\text{Conclusions:}$
- The time function $\text{P}\{ \text{A}\{ x(t)\}\}$ has the period $T_{\rm P} = N \cdot T_{\rm A}$.
- The period in the frequency domain is $f_{\rm P} = N \cdot f_{\rm A}$.
- For the description of the discretized time and frequency response in each case $N$ complex numerical values in the form of impulse weights are sufficient.
$\text{Example 2:}$ A time-limited $($pulse-like$)$ signal $x(t)$ is present in sampled form, where the distance between two samples is $T_{\rm A} = 1\, {\rm µ s}$:
- After a discrete Fourier transform with $N = 512$ the spectrum $X(f)$ is available in form of frequency-samples at spacing $f_{\rm A} = (N \cdot T_{\rm A})^{-1} \approx 1.953\,\text{kHz} $.
- Increasing the DFT parameter to $N= 2048$ results in a $($four times$)$ finer frequency grid with $f_{\rm A} \approx 488\,\text{Hz}$.
From the continuous to the discrete Fourier transform
From the conventional »first Fourier integral«
- $$X(f) =\int_{-\infty }^{+\infty}x(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}t$$
arises from discretization $(\text{d}t \to T_{\rm A}$, $t \to \nu \cdot T_{\rm A}$, $f \to \mu \cdot f_{\rm A}$, $T_{\rm A} \cdot f_{\rm A} = 1/N)$ the sampled and periodified spectral function
- $${\rm P}\{X(\mu \cdot f_{\rm A})\} = T_{\rm A} \cdot \sum_{\nu = 0 }^{N-1} {\rm P}\{x(\nu \cdot T_{\rm A})\}\cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm} \cdot \hspace{0.05cm}\nu \hspace{0.05cm} \cdot \hspace{0.05cm}\mu /N} \hspace{0.05cm}.$$
It is taken into account that due to the discretization, the periodified functions are to be used in each case.
For reasons of simplified notation, we now make the following substitutions:
- The $N$ »time-domain coefficients« are with the variable $\nu = 0$, ... , $N - 1$:
- $$d(\nu) = {\rm P}\left\{x(t)\right\}{\big|}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A}}\hspace{0.05cm}.$$
- Let $N$ »frequency domain coefficients« be associated with the variable $\mu = 0,$ ... , $N-1$:
- $$D(\mu) = f_{\rm A} \cdot {\rm P}\left\{X(f)\right\}{\big|}_{f \hspace{0.05cm}= \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm A}}\hspace{0.05cm}.$$
- Abbreviation is written for the from $N$ dependent »complex rotation factor« :
- $$w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} = \cos \left( {2 \pi}/{N}\right)-{\rm j} \cdot \sin \left( {2 \pi}/{N}\right) \hspace{0.05cm}.$$
$\text{Definition:}$ The term »Discrete Fourier Transform« $\rm (DFT)$ means the calculation of the $N$ spectral coefficients $D(\mu)$ from the $N$ signal coefficients $d(\nu)$:
- $$D(\mu) = \frac{1}{N} \cdot \sum_{\nu = 0 }^{N-1} d(\nu)\cdot {w}^{\hspace{0.05cm}\nu \hspace{0.07cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}. $$
In the diagram you can see:
- The $N = 8$ signal coefficients $d(\nu)$ by the blue filling,
- the $N = 8$ spectral coefficients $D(\mu)$ at the green filling.
Inverse discrete Fourier transform
The »inverse discrete Fourier transform« describes the »second Fourier integral«:
- $$\begin{align*}x(t) & = \int_{-\infty }^{+\infty}X(f) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm} t}\hspace{0.1cm} {\rm d}f\end{align*}$$
in discretized form:
- $$d(\nu) = {\rm P}\left\{x(t)\right\}{\big|}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A}}\hspace{0.01cm}.$$
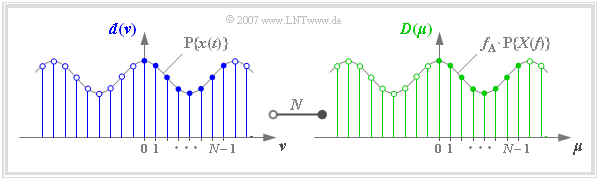
$\text{Definition:}$ The term »Inverse Discrete Fourier Transform» $\rm (IDFT)$ means the calculation of the signal coefficients $d(\nu)$ from the spectral coefficients $D(\mu)$:
- $$d(\nu) = \sum_{\mu = 0 }^{N-1} D(\mu) \cdot {w}^{-\nu \hspace{0.07cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$
- With indices $\nu = 0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, N-1, $ and $\mu = 0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, N-1$ holds:
- $$d(\nu) = {\rm P}\left\{x(t)\right\}{\big \vert}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A} }\hspace{0.01cm},$$
- $$D(\mu) = f_{\rm A} \cdot {\rm P}\left\{X(f)\right\}{\big \vert}_{f \hspace{0.05cm}= \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm A} } \hspace{0.01cm},$$
- $$w = {\rm e}^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} \hspace{0.01cm}.$$
- A comparison between »DFT« and »IDFT« shows that exactly the same algorithm can be used.
- The only differences between IDFT and DFT are:
- The exponent of the rotation factor is to be applied with different sign.
- In the IDFT, the division by $N$ is omitted.
Interpretation of DFT and IDFT
The graph shows the discrete coefficients in the time and frequency domain together with the periodified continuous-time functions.
When using DFT or IDFT, please note:
- According to the above definitions, the DFT coefficients $d(ν)$ and $D(\mu)$ always have the unit of the time function.
- Dividing $D(\mu)$ by $f_{\rm A}$, one obtains the spectral value $X(\mu \cdot f_{\rm A})$.
- The spectral coefficients $D(\mu)$ must always be complex in order to be able to consider odd time functions.
- One also uses complex time coefficients $d(\nu)$ ⇒ DFT and IDFT are also applicable to band-pass signals.
- The basic interval for $\nu$ and $\mu$ is usually defined as the range from $0$ to $N - 1$ $($filled circles in the graph$)$.
With the complex-valued number sequences
- $$\langle \hspace{0.03cm}d(\nu)\hspace{0.03cm}\rangle = \langle \hspace{0.03cm}d(0), \hspace{0.05cm}\text{...} \hspace{0.05cm} , d(N-1) \hspace{0.03cm}\rangle,$$
- $$\langle \hspace{0.03cm}D(\mu)\hspace{0.03cm}\rangle = \langle \hspace{0.03cm}D(0), \hspace{0.05cm}\text{...} \hspace{0.05cm} , D(N-1) \hspace{0.03cm}\rangle,$$
DFT and IDFT are symbolized similarly to the conventional Fourier transform:
- $$\langle \hspace{0.03cm} D(\mu)\hspace{0.03cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.03cm} d(\nu) \hspace{0.03cm}\rangle \hspace{0.05cm}.$$
- If the function $x(t)$ is already limited to the range $0 \le t \lt N \cdot T_{\rm A}$ then the IDFT output directly give the samples of the time function: $d(\nu) = x(\nu \cdot T_{\rm A}).$
- If $x(t)$ is shifted with respect to the basic interval, one has to choose the association shown in $\text{Example 3}$ between $x(t)$ and the coefficients $d(\nu)$.
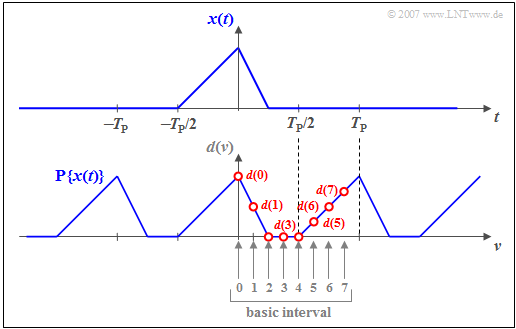
$\text{Example 3:}$ The upper graph shows the asymmetric triangular pulse $x(t)$ whose absolute width is smaller than $T_{\rm P} = N \cdot T_{\rm A}$.
The sketch below shows the assigned DFT coefficients $($valid for $N = 8)$.
- For $\nu = 0,\hspace{0.05cm}\text{...} \hspace{0.05cm} , N/2 = 4$ holds $d(\nu) = x(\nu \cdot T_{\rm A})$ :
- $$d(0) = x (0)\hspace{0.05cm}, \hspace{0.15cm} d(1) = x (T_{\rm A})\hspace{0.05cm}, \hspace{0.15cm} d(2) = x (2T_{\rm A})\hspace{0.05cm}, $$
- $$d(3) = x (3T_{\rm A})\hspace{0.05cm}, \hspace{0.15cm} d(4) = x (4T_{\rm A})\hspace{0.05cm}.$$
- The coefficients $d(5)$, $d(6)$ and d$(7)$ are to be set as follows:
- $$d(5) = x (-3T_{\rm A})\hspace{0.05cm}, \hspace{0.35cm} d(6) = x (-2T_{\rm A})\hspace{0.05cm}, \hspace{0.35cm} d(7) = x (-T_{\rm A})\hspace{0.05cm}$$
- $$ \Rightarrow \hspace{0.2cm}d(\nu) = x \big ((\nu\hspace{-0.05cm} - \hspace{-0.05cm} N ) \cdot T_{\rm A}\big ). $$
Exercises for the chapter
Exercise 5.2: Inverse Discrete Fourier Transform
Exercise 5.2Z: DFT of a Triangular Pulse