Difference between revisions of "Aufgaben:Exercise 5.8Z: Cyclic Prefix and Guard Interval"
| (22 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Modulation_Methods/Implementation_of_OFDM_Systems |
}} | }} | ||
| − | [[File: | + | [[File:EN_Z_5_8.png|right|frame|OFDM scheme with cyclic prefix]] |
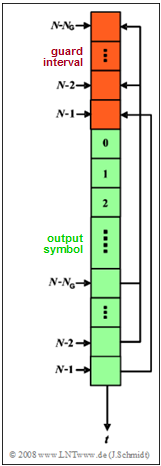
| − | + | In this exercise, we assume an $\rm OFDM$ system with $N = 8$ carriers and cyclic prefix. Let the subcarrier spacing be $f_0 = 4 \ \rm kHz$ ⇒ basic symbol duration: $T=1/f_0$. The diagram shows the principle of the cyclic prefix. | |
| − | + | *Transmission is via a two-way channel, with both paths delayed. The channel impulse response is thus with $τ_1 = \ \rm 50 µs$ and $τ_2 = 125\ \rm µs$: | |
| − | $$ h(t) = h_1 \cdot \delta (t- \tau_1) + h_2 \cdot \delta (t- \tau_2).$$ | + | :$$ h(t) = h_1 \cdot \delta (t- \tau_1) + h_2 \cdot \delta (t- \tau_2).$$ |
| − | + | *However, the use of such a cyclic prefix decreases the bandwidth efficiency $($ratio of symbol rate to bandwidth$)$ by a factor of | |
| − | $$ \beta = \frac{1}{{1 + T_{\rm{G}} /T}} $$ | + | :$$ \beta = \frac{1}{{1 + T_{\rm{G}} /T}} $$ |
| − | + | :and leads also to a reduction of the signal-to-noise ratio by this value $\beta$ as well. | |
| + | *However, a prerequisite for the validity of the SNR loss given here is that the impulse responses $g_{\rm S}(t)$ and $g_{\rm E}(t)$ of the transmit filter (German: "Sendefilter" ⇒ subscript: "S") and the receive filter (German: "Empfangsfilter" ⇒ subscript: "E") are matched to the symbol duration $T$ $($matched–filter approach$)$. | ||
| − | |||
| − | === | + | Notes: |
| + | *The exercise belongs to the chapter [[Modulation_Methods/Realisierung_von_OFDM-Systemen|Implementation of OFDM Systems]]. | ||
| + | *Reference is made in particular to the pages [[Modulation_Methods/Implementation_of_OFDM_Systems#Cyclic_Prefix|Cyclic Prefix]] and [[Modulation_Methods/Implementation_of_OFDM_Systems#OFDM_system_with_cyclic_prefix|OFDM system with cyclic prefix]]. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Specify the basic symbol duration $T$. |
|type="{}"} | |type="{}"} | ||
| − | $T$ | + | $T \ = \ $ { 250 3% } $\ \rm µ s$ |
| − | { | + | {What should be the minimum length of the guard interval $T_{\rm G}$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $T_{\rm G}\ = \ $ { 125 3% } $\ \rm µ s$ |
| − | { | + | {Determine the resulting frame duration $T_{\rm R}$. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $T_{\rm R}\ = \ $ { 375 3% } $\ \rm µ s$ |
| − | { | + | {Which statements are correct? By using a guard gap, i.e. setting the OFDM signal to zero in the guard interval, it is possible to |
|type="[]"} | |type="[]"} | ||
| − | - | + | - suppress intercarrier interference $\rm (ICI)$, |
| − | + | + | + suppress intersymbol interference $\rm (ISI)$. |
| − | { | + | {Which statements are correct? By using a cyclic prefix, i.e. a cyclic extension of the OFDM signal in the guard interval, it is possible to |
|type="[]"} | |type="[]"} | ||
| − | + | + | + suppress intercarrier interference $\rm (ICI)$, |
| − | + | + | + suppress intersymbol interference $\rm (ISI)$. |
| − | { | + | {State the respective number of samples for the basic symbol $(N)$, the guard interval $(N_{\rm G})$ and the entire frame $(N_{\rm R})$. |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $N \hspace{0.35cm} = \ $ { 8 } |
| − | $\ | + | $N_{\rm G} \ = \ $ { 4 } |
| − | + | $N_{\rm R} \ = \ $ { 12 } | |
| − | { | + | {Specify the guard interval samples, assuming that only the first carrier is used with carrier coefficient $-1$. |
|type="{}"} | |type="{}"} | ||
| − | $\text{Re | + | $\text{Re}\big[d_{-1}\big] \ = \ $ { -714--0.700 } |
| − | $\text{Im | + | $\text{Im}\big[d_{-1}\big] \ = \ $ { 0.707 1% } |
| − | $\text{Re | + | $\text{Re}\big[d_{-2}\big] \ = \ $ { 0. } |
| − | $\text{Im | + | $\text{Im}\big[d_{-2}\big] \ = \ $ { 1 1% } |
| − | $\text{Re | + | $\text{Re}\big[d_{-3}\big] \ = \ $ { 0.707 1% } |
| − | $\text{Im | + | $\text{Im}\big[d_{-3}\big] \ = \ $ { 0.707 1% } |
| − | $\text{Re | + | $\text{Re}\big[d_{-4}\big] \ = \ $ { 1 1% } |
| − | $\text{Im | + | $\text{Im}\big[d_{-4}\big] \ = \ $ { 0. } |
| − | { | + | {What is the bandwidth efficiency $\beta$ including the guard interval? |
|type="{}"} | |type="{}"} | ||
| − | $\beta$ | + | $\beta\ = \ $ { 0.667 3% } |
| − | { | + | {What is the associated SNR loss $10 · \lg \ Δρ$ (in dB) assuming the matched filter approach? |
|type="{}"} | |type="{}"} | ||
| − | $10 · lg | + | $10 · \lg \ Δρ \ = \ $ { 1.76 3% } $\ \rm dB$ |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' The basic symbol duration is equal to the reciprocal of the carrier spacing: |
| − | $$ T = | + | :$$ T = {1}/{f_0} \hspace{0.15cm}\underline {= 250\,\,{\rm µ s}}.$$ |
| + | |||
| + | |||
| + | '''(2)''' To avoid interference, the duration $T_{\rm G}$ of the guard interval should be at least as long as the maximum channel delay $($here: $τ_2 = 125\ \rm µ s)$: | ||
| + | :$$ T_{\rm G} \hspace{0.15cm}\underline {= 125\,\,{\rm µ s}}.$$ | ||
| + | |||
| + | |||
| + | '''(3)''' Thus, for the frame duration: | ||
| + | :$$ T_{\rm{R}} = T + T_{\rm G}\hspace{0.15cm}\underline {= 375\,\,{\rm µ s}}.$$ | ||
| + | |||
| + | |||
| + | '''(4)''' <u>Solution 2</u> is correct: | ||
| + | *Only intersymbol interference $\rm (ISI)$ can be avoided by a guard gap of suitable length. | ||
| + | *The gap duration $T_{\rm G}$ must be chosen so large that the current symbol is not affected by the predecessor symbol. | ||
| + | *In the present example, it must be $T_{\rm G}≥ 125\ \rm µ s$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(5)''' <u>Both solutions</u> are applicable: | ||
| + | *A cyclic prefix of suitable length also suppresses intercarrier interference $\rm (ICI)$. | ||
| + | *This ensures that a complete and undistorted oscillation occurs for all carriers within the basic symbol duration $T$, even if other carriers are active. | ||
| − | |||
| − | |||
| − | |||
| − | ''' | + | '''(6)''' The number of samples within the basic symbol is equal to the number of carriers ⇒ $\underline{N=8}$. |
| + | *Because of $T_{\rm G}= T/2$ , $N_{\rm G}\hspace{0.15cm}\underline {= 4}$ and thus $N_{\rm R} = N + N_{\rm G}\hspace{0.15cm}\underline {= 12}$ holds. | ||
| − | |||
| − | |||
| − | '''7 | + | '''(7)''' Assigning the coefficient "-1" to the first carrier $($frequency $f_0)$ results in the samples |
| + | :$$d_0 = -1, \hspace{0.3cm}d_1 = -0.707 - {\rm j} \cdot 0.707, \hspace{0.3cm}d_2 = -{\rm j} ,\hspace{0.3cm} d_3 = +0.707 -{\rm j} \cdot 0.707, $$ | ||
| + | :$$d_4 = +1, \hspace{0.3cm}d_5 = +0.707 + {\rm j} \cdot 0.707, \hspace{0.3cm}d_6 = +{\rm j} ,\hspace{0.3cm} d_7 = -0.707 +{\rm j} \cdot 0.707. $$ | ||
| − | + | *The cyclic expansion provides the additional samples $d_{-1} = d_7$, $d_{-2} = d_6$, $d_{-3} = d_5$ and $d_{-4} = d_4$: | |
| + | :$$\underline{{\rm Re}[d_{-1}] = -0.707,\hspace{0.3cm}{\rm Im}[d_{-1}] = +0.707,\hspace{0.3cm}{\rm Re}[d_{-2}] = 0,\hspace{0.3cm} {\rm Im}[d_{-2}] = 1},$$ | ||
| + | :$$\underline{{\rm Re}[d_{-3}] = +0.707,\hspace{0.3cm}{\rm Im}[d_{-3}] = +0.707,\hspace{0.3cm}{\rm Re}[d_{-4}] = 1,\hspace{0.3cm} {\rm Im}\{d_{-4}] = 0}.$$ | ||
| − | |||
| − | + | '''(8)''' According to the given equation, the bandwidth efficiency is equal to | |
| + | :$$\beta = \frac{1}{1 + {T_{\rm{G}}}/{T}} = \frac{1}{1 + ({125\,\,{\rm \mu s}})/({250\,\,{\rm \mu s}})} \hspace{0.15cm}\underline {= 0.667}.$$ | ||
| − | |||
| − | |||
| − | ''' | + | '''(9)''' The bandwidth efficiency $β = 2/3$ results in an SNR loss of |
| − | + | :$$10 \cdot {\rm{lg}}\hspace{0.04cm}\Delta \rho = 10 \cdot {\rm{lg}}\hspace{0.04cm}(\beta) \hspace{0.15cm}\underline {\approx1.76\,\,{\rm{dB}}}.$$ | |
| − | ''' | ||
| − | $$10 \cdot {\rm{lg}}\hspace{0.04cm}\Delta \rho = 10 \cdot {\rm{lg}}\hspace{0.04cm}(\beta) \hspace{0.15cm}\underline {\approx1.76\,\,{\rm{dB}}}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 103: | Line 126: | ||
| − | [[Category: | + | [[Category:Modulation Methods: Exercises|^5.6 Realization of OFDM Systems^]] |
Latest revision as of 15:52, 31 January 2022
In this exercise, we assume an $\rm OFDM$ system with $N = 8$ carriers and cyclic prefix. Let the subcarrier spacing be $f_0 = 4 \ \rm kHz$ ⇒ basic symbol duration: $T=1/f_0$. The diagram shows the principle of the cyclic prefix.
- Transmission is via a two-way channel, with both paths delayed. The channel impulse response is thus with $τ_1 = \ \rm 50 µs$ and $τ_2 = 125\ \rm µs$:
- $$ h(t) = h_1 \cdot \delta (t- \tau_1) + h_2 \cdot \delta (t- \tau_2).$$
- However, the use of such a cyclic prefix decreases the bandwidth efficiency $($ratio of symbol rate to bandwidth$)$ by a factor of
- $$ \beta = \frac{1}{{1 + T_{\rm{G}} /T}} $$
- and leads also to a reduction of the signal-to-noise ratio by this value $\beta$ as well.
- However, a prerequisite for the validity of the SNR loss given here is that the impulse responses $g_{\rm S}(t)$ and $g_{\rm E}(t)$ of the transmit filter (German: "Sendefilter" ⇒ subscript: "S") and the receive filter (German: "Empfangsfilter" ⇒ subscript: "E") are matched to the symbol duration $T$ $($matched–filter approach$)$.
Notes:
- The exercise belongs to the chapter Implementation of OFDM Systems.
- Reference is made in particular to the pages Cyclic Prefix and OFDM system with cyclic prefix.
Questions
Solution
- $$ T = {1}/{f_0} \hspace{0.15cm}\underline {= 250\,\,{\rm µ s}}.$$
(2) To avoid interference, the duration $T_{\rm G}$ of the guard interval should be at least as long as the maximum channel delay $($here: $τ_2 = 125\ \rm µ s)$:
- $$ T_{\rm G} \hspace{0.15cm}\underline {= 125\,\,{\rm µ s}}.$$
(3) Thus, for the frame duration:
- $$ T_{\rm{R}} = T + T_{\rm G}\hspace{0.15cm}\underline {= 375\,\,{\rm µ s}}.$$
(4) Solution 2 is correct:
- Only intersymbol interference $\rm (ISI)$ can be avoided by a guard gap of suitable length.
- The gap duration $T_{\rm G}$ must be chosen so large that the current symbol is not affected by the predecessor symbol.
- In the present example, it must be $T_{\rm G}≥ 125\ \rm µ s$.
(5) Both solutions are applicable:
- A cyclic prefix of suitable length also suppresses intercarrier interference $\rm (ICI)$.
- This ensures that a complete and undistorted oscillation occurs for all carriers within the basic symbol duration $T$, even if other carriers are active.
(6) The number of samples within the basic symbol is equal to the number of carriers ⇒ $\underline{N=8}$.
- Because of $T_{\rm G}= T/2$ , $N_{\rm G}\hspace{0.15cm}\underline {= 4}$ and thus $N_{\rm R} = N + N_{\rm G}\hspace{0.15cm}\underline {= 12}$ holds.
(7) Assigning the coefficient "-1" to the first carrier $($frequency $f_0)$ results in the samples
- $$d_0 = -1, \hspace{0.3cm}d_1 = -0.707 - {\rm j} \cdot 0.707, \hspace{0.3cm}d_2 = -{\rm j} ,\hspace{0.3cm} d_3 = +0.707 -{\rm j} \cdot 0.707, $$
- $$d_4 = +1, \hspace{0.3cm}d_5 = +0.707 + {\rm j} \cdot 0.707, \hspace{0.3cm}d_6 = +{\rm j} ,\hspace{0.3cm} d_7 = -0.707 +{\rm j} \cdot 0.707. $$
- The cyclic expansion provides the additional samples $d_{-1} = d_7$, $d_{-2} = d_6$, $d_{-3} = d_5$ and $d_{-4} = d_4$:
- $$\underline{{\rm Re}[d_{-1}] = -0.707,\hspace{0.3cm}{\rm Im}[d_{-1}] = +0.707,\hspace{0.3cm}{\rm Re}[d_{-2}] = 0,\hspace{0.3cm} {\rm Im}[d_{-2}] = 1},$$
- $$\underline{{\rm Re}[d_{-3}] = +0.707,\hspace{0.3cm}{\rm Im}[d_{-3}] = +0.707,\hspace{0.3cm}{\rm Re}[d_{-4}] = 1,\hspace{0.3cm} {\rm Im}\{d_{-4}] = 0}.$$
(8) According to the given equation, the bandwidth efficiency is equal to
- $$\beta = \frac{1}{1 + {T_{\rm{G}}}/{T}} = \frac{1}{1 + ({125\,\,{\rm \mu s}})/({250\,\,{\rm \mu s}})} \hspace{0.15cm}\underline {= 0.667}.$$
(9) The bandwidth efficiency $β = 2/3$ results in an SNR loss of
- $$10 \cdot {\rm{lg}}\hspace{0.04cm}\Delta \rho = 10 \cdot {\rm{lg}}\hspace{0.04cm}(\beta) \hspace{0.15cm}\underline {\approx1.76\,\,{\rm{dB}}}.$$