Aufgaben:Exercise 5.5: Fast Fourier Transform

• Return to book

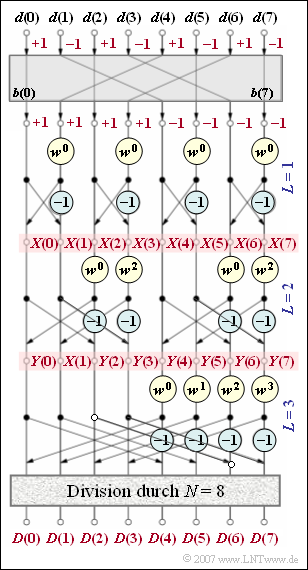
Die Grafik zeigt den Signalflussplan der DFT für $N = 8$. Aus den Zeitkoeffizienten $d(0), ... , d(7)$ werden die dazugehörigen Spektralkoeffizienten $D(0), ... , D(7)$ ermittelt. Für diese gilt mit $0 ≤ μ ≤ 7$:

$$D(\mu) = \frac{1}{N}\cdot \sum_{\nu = 0 }^{N-1} d(\nu) \cdot {w}^{\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu}\hspace{0.05cm},$$

wobei der komplexe Drehfaktor $w = \text{exp}^{–\text{j}2\pi /N}$ zu verwenden ist, also $w = \text{exp}^{–\text{j}\pi /4}$ für $N = 8$.

Am Eingang wird die alternierende $±1$–Folge $\langle d(ν)\rangle$ angelegt. Nach der Bitumkehroperation ergibt sich daraus die Folge $\langle b(\kappa)\rangle$.

Es gilt $b(κ) = d(ν)$, wenn man $ν$ als Dualzahl darstellt und die resultierenden drei Bit als $κ$ in umgekehrter Reihenfolge geschrieben werden. Beispielsweise

• folgt aus $ν = 1$ (binär 001) die Position $κ = 4$ (binär 100),
• verbleibt $d(2)$ an der gleichen Position $2$ (binär 010).

Der eigentliche FFT–Algorithmus geschieht für das Beispiel $N = 8$ in $\log_2 N = 3$ Stufen, die mit $L = 1$, $2$ und $3$ bezeichnet werden. Weiter gilt:

• In jeder Stufe sind vier Basisoperationen – so genannte Butterflies – durchzuführen.
• Die Werte am Ausgang der ersten Stufe werden in dieser Aufgabe mit $X(0), ... , X(7)$ bezeichnet, die der zweiten mit $Y(0), ... , Y(7)$.
• Nach der dritten und letzten Stufe sind alle Werte noch durch $N$ zu dividieren.

Hinweise:

• Die Aufgabe gehört zum Kapitel Fast-Fouriertransformation (FFT).
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Berechnen Sie den DFT–Koeffizienten $D(3)$.

$D(3) =$

2

Berechnen Sie den DFT–Koeffizienten $D(4)$.

$D(4) =$

3

Ermitteln Sie die Ausgangswerte $X(0), ... , X(7)$ der ersten Stufe. Welche der folgenden Aussagen sind zutreffend?

	Alle Werte mit geradzahligen Indizes sind gleich $2$.
	Alle Werte mit ungeradzahligen Indizes sind gleich $0$.

4

Ermitteln Sie die Ausgangswerte $Y(0), ... , Y(7)$ der zweiten Stufe. Geben Sie zur Kontrolle die Werte $Y(0)$und $Y(4)$ ein.

$Y(0) =$

$Y(4) =$

5

Berechnen Sie alle $N$ Spektralwerte $D(\mu)$, insbesondere

$D(\mu = 4) =$

$D(\mu = 4) =$

$D(\mu \neq 4) =$

6

Welche Spektralkoeffizienten würden sich für $d(ν = 4) = 1$ und $d(ν \neq 4) = 0$ ergeben? Geben Sie zur Kontrolle die Werte $D(3)$ und $D(4)$ ein:

$D(\mu = 3) =$

$D(\mu = 4) =$

Musterlösung

Solution

1. Entsprechend der auf dem Angabenblatt gegebenen allgemeinen DFT–Gleichung gilt mit $w = \text{exp}(–\text{j}\pi /4)$ unter Berücksichtigung der alternierenden Zeitkoeffizienten:

$$\begin{align*}8 \cdot D(3) & = w^0 - w^3 + w^6- w^9+ w^{12}- w^{15}+ w^{18}- w^{21} \\ & = w^0 - w^3 + w^2- w^1+ w^{4}- w^{7}+ w^{6}- w^{5}\hspace{0.05cm}.\end{align*}$$

Hierbei ist berücksichtigt, dass aufgrund der Periodizität $w_9 = w_1$, $w_{12} = w_4$, $w_{15} = w_7$, $w_{18} = w_2$ und $w_{21} = w_5$ ist. Nach Umsortieren gilt in gleicher Weise

$$\begin{align*} 8 \cdot D(3) & = (w^0 + w^4) - (w^1 + w^5)+ (w^2 + w^6) - (w^3 + w^7) = \\ & = (1 + w + w^2+ w^3) \cdot (w^0 + w^4)\hspace{0.05cm}.\end{align*}$$

Wegen $w_0 = 1$ und $w_4 = \text{exp}(–\text{j} \cdot \pi) = –1$ erhält man somit $D$(3) = 0.

2. In analoger Weise zu 1) ergibt sich nun:

$$\begin{align*} 8 \cdot D(4) & = w^0 - w^4 + w^8- w^{12}+ w^{16}- w^{20}+ w^{24}- w^{28}= \\ & = 4 \cdot (w^0 - w^4)= 8 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\hspace{0.15 cm}\underline{D(4) = 1}\hspace{0.05cm}.\end{align*}$$

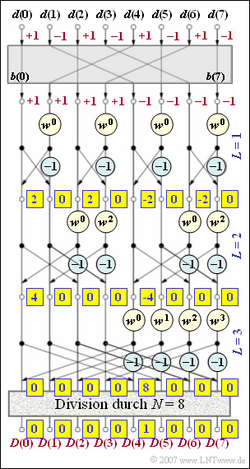
3. Der Term $w_0$ = 1 muss nicht berücksichtigt werden. Alle Ausgangswerte mit ungeraden Indizes sind somit durch die Subtraktion zweier identischer Eingangswerte gleich 0. Die erste Aussage trifft dagegen nicht zu: Es gilt $X$(0) = $X$(2) = +2 und $X$(4) = $X$(6) = –2 ⇒ Lösungsvorschlag 2.

4. Auf die Multiplikation mit $w_2$ = –j kann verzichtet werden, da im Signalflussplan die entsprechenden Eingangsgrößen 0 sind. Man erhält somit $Y$(0) = 4 und $Y$(4) = –4. Alle anderen Werte sind 0.

5. Wegen $Y$(5) = $Y$(6) =$Y$(7) = 0 spielen auch in der dritten Stufe die Multiplikationen mit $w$, $w_2$ und $w_3$ keine Rolle. Alle Spektralkoeffizienten $D(\mu)$ ergeben sich zu 0 mit Ausnahme von

$$\hspace{0.15 cm}\underline{D(4)} = {1}/{N}\cdot \left[Y(0) - Y(4) \right ] \hspace{0.15 cm}\underline{= 1} \hspace{0.05cm}.$$

Dieses Ergebnis stimmt mit den Ergebnissen aus 1) und 2) überein.

6. Nachdem sowohl die Zeitkoeffizienten $d(ν)$ als auch alle Spektralkoeffizienten $D(\mu)$ rein reell sind, besteht kein Unterschied zwischen der FFT und der IFFT. Das bedeutet gleichzeitig: die Eingangs– und Ausgangswerte können vertauscht werden. Die Teilaufgabe 5) hat das folgende Ergebnis geliefert:

$$d({\rm gerades}\hspace{0.15cm}\nu) = +1, \hspace{0.2cm}d({\rm ungerades}\hspace{0.15cm}\nu)= -1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}D(\mu = 4)= 1,\hspace{0.2cm}D(\mu \ne 4)= 0.$$

Durch Vertauschen der Eingangs– und Ausgangswerte kommt man zur Aufgabenstellung von (6):

$$d(\nu = 4)= 1, \hspace{0.2cm}d(\nu \ne 4)= 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}D({\rm gerades}\hspace{0.15cm}\mu) = +1, \hspace{0.2cm}D({\rm ungerades}\hspace{0.15cm}\mu)= -1 \hspace{0.05cm}.$$

Insbesondere würde sich $D$(3) = –1 und D(4) = +1 ergeben.