Difference between revisions of "Aufgaben:Exercise 2.5: Distortion and Equalization"

From LNTwww
Line 45: Line 45:
  
  
−
{Welche Eigenschaften zeigt das System beim Testsignal <i>x</i><sub>1</sub>(<i>t</i>) mit <i>f</i><sub>2</sub> = 4 kHz?
+
{Welche Eigenschaften zeigt das System beim Testsignal $x_1(t)$ mit $f_2 = 4 \ \rm kHz$?
 
|type="[]"}
 
|type="[]"}
 
+ Es wirkt wie ein ideales System.
 
+ Es wirkt wie ein ideales System.
Line 52: Line 52:
  
  
−
{Welche Eigenschaften zeigt das System beim Testsignal <i>x</i><sub>1</sub>(<i>t</i>) mit <i>f</i><sub>2</sub> = 10 kHz?
+
{Welche Eigenschaften zeigt das System beim Testsignal $x_1(t)$ mit $f_2 = 10 \ \rm kHz$?
 
|type="[]"}
 
|type="[]"}
 
- Es wirkt wie ein ideales System.
 
- Es wirkt wie ein ideales System.
Line 59: Line 59:
  
  
−
{Wie groß ist die die Maximalabweichung <i>&epsilon;</i><sub>max</sub> =  
+
{Wie groß ist beim Testsignal $x_2(t)$  mit $f_0 = 3 \ \rm kHz$ die Maximalabweichung $\varepsilon_{\rm max} = |y_2(t_0) - x_2(t_0)|$. An welcher Stelle $t_0$ tritt $\varepsilon_{\rm max}|$ auf?
−
|<i>y</i><sub>2</sub>(<i>t</i>) &ndash; <i>x</i><sub>2</sub>(<i>t</i>)| beim Signal <i>x</i><sub>2</sub>(<i>t</i>) mit <i>f</i><sub>0</sub> = 3 kHz? An welcher Stelle <i>t</i><sub>0</sub> tritt diese Abweichung auf?
 
 
|type="{}"}
 
|type="{}"}
−
$f_0 = 3 kHz:\ \ \epsilon_\text{max}$ = { 0.156 3% } $V$
+
$f_0 = 3\ \rm kHz$: &nbsp;&nbsp; $\varepsilon_\text{max} \ = $ { 0.156 3% } $\ \rm V$
−
$t_0$ = { 0 3% } $ms$
+
$t_0 \ = $ { 0. } $\ \rm ms$
  
  
−
{Wie groß ist die maximale Abweichung mit <i>f</i><sub>0</sub> = 2 kHz?
+
{Wie groß ist die maximale Abweichung $\varepsilon_{\rm max}|$ mit $f_0 = 2 \ \rm kHz$?
 
|type="{}"}
 
|type="{}"}
−
$f_0 = 2 kHz:\ \ \epsilon_\text{max}$ = { 0.114 3% } $V$
+
$f_0 = 2\ \rm kHz$: &nbsp;&nbsp; $\varepsilon_\text{max} \ = $ { 0.114 3% } $\ \rm V$
  
  
−
{Welchen Verlauf sollte der Entzerrer <i>H</i><sub>E</sub>(<i>f</i>) besitzen, um alle Verzerrungen von <i>H</i>(<i>f</i>) bestmöglich zu kompensieren. Welcher Wert ergibt sich bei <i>f</i> = 10 kHz?
+
{Welchen Verlauf sollte der Entzerrer $H_{\rm E}(f)$ besitzen, um alle Verzerrungen von $H(f)$ bestmöglich zu kompensieren. Welcher Betragswert ergibt sich bei $f = 10 \ \rm kHz$?
 
|type="{}"}
 
|type="{}"}
−
$|H_E(f = 10 kHz)|$ = { 4 3% }
+
$|H_E(f = 10 \ \rm kHz)| \ = $ { 4 3% }
  
  
−
{Bei welchen der nachfolgenden Signale ist eine vollständige Entzerrung möglich? Unter vollständiger Entzerrung soll dabei <i>z</i>(<i>t</i>) = <i>x</i>(<i>t</i>) verstanden werden.
+
{Bei welchen der aufgeführten Signale ist eine vollständige Entzerrung möglich? Unter vollständiger Entzerrung soll dabei $z(t) = x(t)$ verstanden werden.
 
|type="[]"}
 
|type="[]"}
−
+ Beim Signal <i>x</i><sub>1</sub>(<i>t</i>) mit <i>f</i><sub>2</sub> = 10 kHz.
+
+ Beim Signal $x_1(t)$ mit $f_2 = 10 \ \rm kHz$.
−
- Beim Signal <i>x</i><sub>2</sub>(<i>t</i>).
+
- Beim Signal $x_2(t)$.
−
- Beim Signal <i>x</i><sub>3</sub>(<i>t</i>).
+
- Beim Signal $x_3(t)$.
  
  

Revision as of 16:44, 2 February 2017

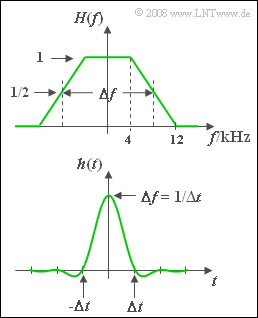
Trapezspektrum und zugehörige Impulsantwort

Betrachtet wird ein Nachrichtensystem mit Eingang $x(t)$ und Ausgang $y(t)$ , das durch den trapezförmigen Frequenzgang $H(f)$ gemäß der oberen Grafik vollständig beschrieben wird. Mit dem Rolloff–Faktor $r = 0.5$ sowie der äquivalenten Bandbreite $\Delta f = 16 \ \rm kHz$ lautet die dazugehörige, über die Fourierrücktransformation berechenbare Impulsantwort: $$h(t) = \Delta f \cdot {\rm si}(\pi \cdot \Delta f \cdot t )\cdot {\rm si}(\pi \cdot r \cdot \Delta f \cdot t ) .$$

Als Eingangssignale stehen zur Verfügung:

  • Die Summe zweier harmonischer Schwingungen:
$$x_1(t) = {1\, \rm V} \cdot \cos(\omega_1 \cdot t) + {1\, \rm V} \cdot \sin(\omega_2 \cdot t).$$
Hierbei gelte für $\omega_1 = 2\pi; \cdot 2000 \ {\rm 1/s}$ und $\omega_2 \gt \omega_1$.
  • Ein periodisches Dreiecksignal:
$$x_2(t) = \frac{8\, \rm V}{\pi^2} \cdot \left[\cos(\omega_0 t) + {1}/{9} \cdot \cos(3\omega_0 t) + {1}/{25} \cdot \cos(5\omega_0 t) + \hspace{0.05cm}...\right].$$
Es ist anzumerken, dass die Grundfrequenz $f_0 = 2 \ \rm kHz$ bzw. $3\ \rm kHz$ beträgt. Zum Zeitpunkt $t = 0$ ist der Signalwert in beiden Fällen $1 \ \rm V$.
  • Ein Rechteckimpuls $x_3(t)$ mit Amplitude $A = 1 \ \rm V$ und Dauer $T = 1 \ \rm ms$. Da dessen Spektrum $X_3(f)$ bis ins Unendliche reicht, führt $H(f)$ hier immer zu linearen Verzerrungen.


Ab der Teilaufgabe (6) soll versucht werden, durch einen nachgeschalteten Entzerrer mit

  • Frequenzgang $H_{\rm E}(f)$,
  • Eingangssignal $y(t)$, und
  • Ausgangssignal $z(t)$

die eventuell von $H(f)$ erzeugten Verzerrungen zu eliminieren.

Hinweise:

  • Die Aufgabe gehört zum Kapitel Lineare Verzerrungen.
  • Der im Fragenkatalog verwendete Begriff „Gesamtverzerrung” bezieht sich auf das Eingangssignal $x(t)$ und das Ausgangssignal $z(t)$.
  • Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.


Fragebogen

1

Welche Verzerrungsarten können bei diesem System ausgeschlossen werden?

Nichtlineare Verzerrungen.
Dämpfungsverzerrungen.
Phasenverzerrungen.

2

Welche Eigenschaften zeigt das System beim Testsignal $x_1(t)$ mit $f_2 = 4 \ \rm kHz$?

Es wirkt wie ein ideales System.
Es wirkt wie ein verzerrungsfreies System.
Man erkennt, dass ein verzerrendes System vorliegt.

3

Welche Eigenschaften zeigt das System beim Testsignal $x_1(t)$ mit $f_2 = 10 \ \rm kHz$?

Es wirkt wie ein ideales System.
Es wirkt wie ein verzerrungsfreies System.
Man erkennt, dass ein verzerrendes System vorliegt.

4

Wie groß ist beim Testsignal $x_2(t)$ mit $f_0 = 3 \ \rm kHz$ die Maximalabweichung $\varepsilon_{\rm max} = |y_2(t_0) - x_2(t_0)|$. An welcher Stelle $t_0$ tritt $\varepsilon_{\rm max}|$ auf?

$f_0 = 3\ \rm kHz$:    $\varepsilon_\text{max} \ = $

$\ \rm V$
$t_0 \ = $

$\ \rm ms$

5

Wie groß ist die maximale Abweichung $\varepsilon_{\rm max}|$ mit $f_0 = 2 \ \rm kHz$?

$f_0 = 2\ \rm kHz$:    $\varepsilon_\text{max} \ = $

$\ \rm V$

6

Welchen Verlauf sollte der Entzerrer $H_{\rm E}(f)$ besitzen, um alle Verzerrungen von $H(f)$ bestmöglich zu kompensieren. Welcher Betragswert ergibt sich bei $f = 10 \ \rm kHz$?

$|H_E(f = 10 \ \rm kHz)| \ = $

7

Bei welchen der aufgeführten Signale ist eine vollständige Entzerrung möglich? Unter vollständiger Entzerrung soll dabei $z(t) = x(t)$ verstanden werden.

Beim Signal $x_1(t)$ mit $f_2 = 10 \ \rm kHz$.
Beim Signal $x_2(t)$.
Beim Signal $x_3(t)$.


Musterlösung

Solution

1.  Durch die Angabe eines Frequenzgangs wird bereits implizit ein lineares System vorausgesetzt, so dass nichtlineare Verzerrungen nicht auftreten können. Da H(f) rein reell ist, können Phasenverzerrungen ebenfalls ausgeschlossen werden  ⇒  Lösungsvorschläge 1 und 3.
2.  Das Ausgangssignal ist y1(t) = x1(t). Somit ist das System nicht nur verzerrungsfrei, sondern kann für diese Anwendung auch als ideal bezeichnet werden. Richtig sind also die Alternativen 1 und 2.
3.  In diesem Fall erhält man das Ausgangssignal:
$$y_1(t)= 1\,{\rm V}\cdot \cos(2 \pi \cdot f_1 \cdot t) + \frac{1}{4}\cdot 1\,{\rm V}\cdot \sin(2 \pi \cdot f_2 \cdot t).$$
Während der Anteil bei f1 unverändert übertragen wird, ist der Sinusanteil mit f2 auf ein Viertel gedämpft. Also liegen Dämpfungsverzerrungen vor  ⇒  Antwort 3.
4.  Das Ausgangssignal y2(t) hat folgende Form, wenn man die Grundfrequenz f0 = 3 kHz berücksichtigt:
$$y_2(t)= \frac{8\,{\rm V}}{\pi^2} \left( \cos(\omega_0 t) + \frac{3}{8}\cdot \frac{1}{9} \cdot \cos(3\omega_0 t)\right) .$$
Der Faktor 3/8 beschreibt H(f = 9 kHz). Alle weiteren Spektralanteile bei 15 kHz, 21 kHz usw. werden vom System unterdrückt.
Die stärksten Abweichungen zwischen x2(t) und y2(t) wird es bei den Dreieckspitzen geben, da sich hier die fehlenden hohen Frequenzen am stärksten auswirken. Zum Beispiel erhält man für t = t0 = 0:
$$y_2(t=0)= \frac{8\,{\rm V}}{\pi^2} \left( 1 + \frac{3}{72}\right)= 0.844\,{\rm V}$$
$$\Rightarrow\hspace{0.3cm} \varepsilon_{\rm max} = |y_2(t=0)- x_2(t=0)| \hspace{0.15cm}\underline{= 0.156\,{\rm V}}.$$
5.  Mit der Grundfrequenz f0 = 2 kHz, H(3f0) = 0.75, H(5f0) = 0.25 und H(7f0) = 0 ergibt sich:
$$y_2(t=0)= \frac{8\,{\rm V}}{\pi^2} \left( 1 + \frac{3}{4}\cdot \frac{1}{9} + \frac{1}{4} \cdot\frac{1}{25}\right)= 0.886\,{\rm V}\hspace{0.5cm} \Rightarrow \hspace{0.5cm}\varepsilon_{\rm max} \hspace{0.15cm}\underline{= 0.114\,{\rm V}}.$$
6.  Im Bereich bis 4 kHz ist HE(f) = H(f) = 1 zu sehen. Dagegen gilt im Bereich von 4 kHz bis 12 kHz:
$$H_{\rm E}(f)= \frac{1}{H(f)} = \frac{1}{1.5 \cdot [1 - f/(12\,{\rm kHz})]} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} H_{\rm E}(f = 10\,{\rm kHz})\hspace{0.15cm}\underline{= 4} .$$
Der Nennerausdruck beschreibt hierbei die Geradengleichung des Flankenabfalls.
7.  Sowohl x2(t) als auch x3(t) beinhalten Spektralanteile bei Frequenzen größer als 12 kHz. Wurden diese durch die Bandbegrenzung von H(f) abgeschnitten, so können sie durch den Entzerrer nicht mehr rekonstruiert werden. Das heißt, dass nur das Signal x1(t) durch HE(f) wieder hergestellt werden kann:
$$z_1(t)= 1 \cdot 1\,{\rm V}\cdot \cos(2 \pi \cdot f_1 \cdot t) + 4 \cdot \frac{1}{4}\cdot 1\,{\rm V}\cdot \sin(2 \pi \cdot f_2 \cdot t).$$
Die jeweils ersten Faktoren geben jeweils die Verstärkung von HE(f) an  ⇒  Antwort 1.

Retrieved from "http://en.lntwww.de/index.php?title=Aufgaben:Exercise_2.5:_Distortion_and_Equalization&oldid=11135"
  • Powered by MediaWiki