Aufgaben:Exercise 1.1Z: Sum of Two Ternary Signals

• Return to book

Summe zweier Ternärsignale

Gegeben seien zwei dreistufige Nachrichtenquellen $X$ und $Y$, deren Ausgangssignale jeweils nur die Werte $–1$, $0$ und $+1$ annehmen können. Die Signalquellen sind statistisch voneinander unabhängig.

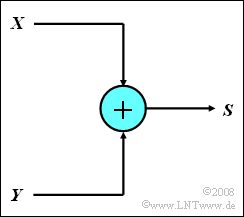
• Eine einfache Schaltung bildet nun das Summensignal $S = X + Y$.
• Bei der Signalquelle $X$ treten die Werte $–1$, $0$ und $+1$ mit gleicher Wahrscheinlichkeit auf.
• Bei der Quelle ist $Y$ der Signalwert $0$ doppelt so wahrscheinlich wie die beiden anderen Werte $–1$ bzw. $+1$.

Hinweise:

• Die Aufgabe gehört zum Kapitel Einige grundlegende Definitionen der Wahrscheinlichkeitsrechnung.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Lösen Sie die Teilaufgaben (3) und (4) nach der klassischen Definition. Berücksichtigen Sie trotzdem die unterschiedlichen Auftrittshäufigkeiten des Signals $Y$.
• Der Inhalt dieses Abschnitts ist in einem Lernvideo zusammengefasst:

Klassische Definition der Wahrscheinlichkeit

Fragebogen

1

Wie groß sind die Auftrittswahrscheinlichkeiten der Signalwerte von $Y$? Wie groß ist die Wahrscheinlichkeit, dass $Y = 0$ ist ?

$Pr(Y=0) \ = $

2

Wieviele unterschiedliche Signalwerte $(I)$ kann das Summensignal $S$ annehmen? Welche sind dies?

$ I \ = $

3

Mit welchen Wahrscheinlichkeiten treten die in der Teilaufgabe (2) ermittelten Werte auf? Wie wahrscheinlich ist der Maximalwert $S_{\rm max}$?

$ Pr(S = S_{\rm max} ) \ = $

4

Wie ändern sich die Wahrscheinlichkeiten, wenn nun anstelle der Summe die Differenz $D = X - Y$ betrachtet wird? Begründen Sie Ihre Antwort.

	Die Wahrscheinlichkeiten bleiben gleich.
	Die Wahrscheinlichkeiten ändern sich. Wie ändern sie sich?

Musterlösung

Solution

(1)  Da die Wahrscheinlichkeiten von $ \pm 1$ gleich sind und ${\rm Pr}(Y = 0) = 2 \cdot {\rm Pr}(Y = 1)$ gilt, erhält man:

$${\rm Pr}(Y = 1) + {\rm Pr}(Y = 0) + {\rm Pr}(Y = -1) = 1/2 \cdot {\rm Pr}(Y = 0) + {\rm Pr}(Y = 0) + 1/2\cdot {\rm Pr}(Y = 0) = 1\hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm Pr}(Y = 0)\;\underline { = 1/2}. $$

(2)  $S$ kann insgesamt $\underline {I =5}$ Werte annehmen, nämlich $0$, $\pm 1$ und $\pm 2$.

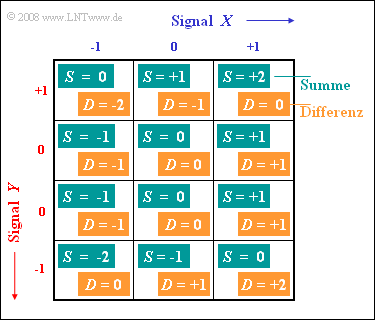
(3)  Da $Y$ nicht gleichverteilt ist, kann man hier (eigentlich)die „Klassische Definition der Wahrscheinlichkeit” nicht anwenden. Teilt man $Y$ jedoch gemäß der Grafik in vier Bereiche auf, wobei man zwei der Bereiche dem Ereignis $Y = 0$ zuordnet, so kann man die klassische Definition dennoch anwenden. Man erhält dann:

$${\rm Pr}(S = 0) = {4}/{12} = {1}/{3},$$ $${\rm Pr}(S = +1) = {\rm Pr}(S = -1) ={3}/{12} = {1}/{4},$$ $${\rm Pr}(S = +2) = {\rm Pr}(S = -2) ={1}/{12}$$ $$\Rightarrow \hspace{0.3cm}{\rm Pr}(S = S_{\rm max}) = {\rm Pr}(S = +2) =1/12 \;\underline {= 0.0833}.$$

(4)  Aus der Grafik ist auch ersichtlich, dass das Differenzsignal $D$ und das Summensignal $S$ die gleichen Werte mit gleichen Wahrscheinlichkeiten annehmen. Dies war zu erwarten, da ${\rm Pr}(Y = +1) ={\rm Pr}(Y = -1)$ vorgegeben ist ⇒ Lösungsvorschlag 1.