Difference between revisions of "Aufgaben:Exercise 5.9: Minimization of the MSE"
From LNTwww
| Line 4: | Line 4: | ||
[[File:P_ID652__Sto_A_5_9.png|right|Leistungsdichtespektren beim Wiener-Filter ]] | [[File:P_ID652__Sto_A_5_9.png|right|Leistungsdichtespektren beim Wiener-Filter ]] | ||
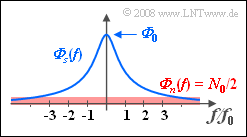
| − | Gegeben ist | + | Gegeben ist ein stochastisches Nutzsignal $s(t)$, von dem nur das Leistungsdichtespektrum (LDS) bekannt ist: |
:$${\it \Phi} _s (f) = \frac{\it{\Phi} _{\rm 0} }{1 + ( {f/f_0 } )^2 }.$$ | :$${\it \Phi} _s (f) = \frac{\it{\Phi} _{\rm 0} }{1 + ( {f/f_0 } )^2 }.$$ | ||
| − | Dieses ist in der nebenstehenden Grafik blau dargestellt. | + | Dieses LDS ${\it \Phi} _s (f)$ ist in der nebenstehenden Grafik blau dargestellt. |
*Die mittlere Leistung von $s(t)$ ergibt sich durch Integration über das Leistungsdichtespektrum: | *Die mittlere Leistung von $s(t)$ ergibt sich durch Integration über das Leistungsdichtespektrum: | ||
Revision as of 10:56, 24 April 2017
Gegeben ist ein stochastisches Nutzsignal $s(t)$, von dem nur das Leistungsdichtespektrum (LDS) bekannt ist:
- $${\it \Phi} _s (f) = \frac{\it{\Phi} _{\rm 0} }{1 + ( {f/f_0 } )^2 }.$$
Dieses LDS ${\it \Phi} _s (f)$ ist in der nebenstehenden Grafik blau dargestellt.
- Die mittlere Leistung von $s(t)$ ergibt sich durch Integration über das Leistungsdichtespektrum:
- $$P_s = \int_{ - \infty }^{ + \infty } {{\it \Phi} _s (f)}\, {\rm d} f = {\it \Phi} _0 \cdot f_0 \cdot {\rm{\pi }}.$$
- Additiv überlagert ist dem Nutzsignal $s(t)$ weißes Rauschen mit der Rauschleistungsdichte ${\it \Phi}_n(f) = N_0/2$
- Als Abkürzung verwenden wir $Q = 2 \cdot {\it \Phi}_0/N_0$, wobei $Q$ als „Qualität” interpretiert werden kaönnte.
- Zu beachten ist, dass $Q$ kein Signal–zu–Rauschleistungsverhältnis darstellt.
In dieser Aufgabe soll der Frequenzgang$H(f)$ eines Filters ermittelt werden, das den mittleren quadratischen Fehler (MQF) zwischen dem Nutzsignal $s(t)$ und dem Filterausgangssignal $d(t)$ minimiert:
- $${\rm{MQF}} = \mathop {\lim }\limits_{T_{\rm M} \to \infty } \frac{1}{T_{\rm M} }\int_{ - T_{\rm M} /2}^{T_{\rm M} /2} {\left| {d(t) - s(t)} \right|^2 \, {\rm{d}}t.}$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Matched-Filter.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Verwenden Sie für numerische Berechnungen stets die Zahlenwerte
- $$G_0 = 10^{ - 4} \;{\rm{V/Hz}}{\rm{, }}\quad \Delta f = 10\;{\rm{kHz}}.$$
- Hinweis: Die Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 5.5. Zur Lösung vorgegeben wird das folgende unbestimmte Integral:
- $$\int {\frac{1}{a^2 + x^2 }} \, {\rm{d}}x = \frac{1}{a} \cdot \arctan \left( {\frac{x}{a}} \right).$$
Fragebogen
Musterlösung
- 1. Richtig ist hier nur der letzte Lösungsvorschlag. Die Aufgabenstellung („Minimierung des mittleren quadratischen Fehlers”) weist bereits auf das Filter nach Wiener–Kolmogorow hin. Das Matched–Filter verwendet man dagegen, um die Signalenergie zu bündeln und dadurch für einen vorgegebenen Zeitpunkt das S/N–Verhältnis zu maximieren.
- 2. Für den optimalen Frequenzgang gilt nach Wiener und Kolmogorow allgemein:
- $$H(f) = H_{\rm WF} (f) = \frac{1}{{1 + {\it \Phi} _n (f)/{\it \Phi} _s (f)}}.$$
- Mit den gegebenen Leistungsdichtespektren kann hierfür auch geschrieben werden:
- $$H(f) = \frac{1}{{1 + {N_0 }/({{2{\it \Phi} _0 })}\cdot \left[ {1 + ( {f/f_0 } )^2 } \right]}} = \frac{1}{{1 + {1}/{Q}\cdot \left[ {1 + ( {f/f_0 } )^2 } \right]}}.$$
- Mit Q = 3 folgt daraus:
- $$H( {f = 0} ) = \frac{1}{{1 + {1}/{Q}}} = \frac{Q}{Q + 1} \hspace{0.15cm}\underline {= 0.75},$$
- $$H( {f = 2f_0 } ) = \frac{1}{{1 + {5}/{Q}}} = \frac{Q}{Q + 5} \hspace{0.15cm}\underline {= 0.375}.$$
- 3. Für das unter b) berechnete Filter gilt unter Berücksichtigung der Symmetrie:
- $${\rm{MQF = }}\int_{-\infty}^{+\infty} H(f) \cdot {\it \Phi} _n (f) \,\, {\rm{d}}f = \int_{0}^{+\infty} \frac{N_0}{{1 + {N_0 }/({{2{\it \Phi} _0 })}\cdot \left[ {1 + ( {f/f_0 } )^2 } \right]}} \,\, {\rm{d}}f .$$
- Hierfür kann mit Q = 2Φ0 / N0 und a2 = Q + 1 auch geschrieben werden:
- $${\rm{MQF = }}\int_0^\infty {\frac{{2{\it \Phi} _0 }}{{ Q+1 + ( {f/f_0 })^2 }}} \,\, {\rm{d}}f = 2{\it \Phi} _0 \cdot f_0 \int_0^\infty {\frac{1}{a^2 + x^2 }}\,\, {\rm{d}}x.$$
- Mit dem angegebenen Integral führt dies zum Ergebnis:
- $${\rm{MQF}} = \frac{{2{\it \Phi} _0 f_0 }}{{\sqrt {1 + Q} }}\left( {\arctan ( \infty ) - \arctan ( 0 )} \right) = \frac{{{\it \Phi} _0 f_0 {\rm{\pi }}}}{{\sqrt {1 + Q} }}.$$
- Normiert man MQF auf die Nutzleistung Ps, so erhält man für Q = 3:
- $$\frac{\rm{MQF}}{P_s} = \frac{1}{{\sqrt {1 + Q} }} \hspace{0.15cm}\underline { = 0.5}.$$
- 4. Aus der Berechnung in (c) folgt für MQF/Ps ≤ 0.1 direkt die Bedingung Q ≥ 99 ⇒ Qmin = 99. Je größer Q ist, desto kleiner wird der mittlere quadratische Fehler.
- 5. Ein zum Wiener–Kolmogorow–Filterr formgleicher Frequenzgang ⇒ H(f) = K · HWF(f) mit K ≠ 1 führt stets zu großen Verfälschungen. Dies kann man sich zum Beispiel am rauschfreien Fall (Q → ∞) verdeutlichen. In diesem Fall wäre d(t) = K · s(t) und die Optimierungsaufgabe trotz guter Bedingungen extrem schlecht gelöst.
- Aus der Gleichung
- $${\rm{MQF}} = \int_{ - \infty }^{ + \infty } {H_{\rm WF} (f)} \cdot \it{\Phi} _n (f)\,\,{\rm{d}}f$$
- könnte man fälschlicherweise schließen, dass durch ein Filter H(f) = 2 · HWF(f) der mittlere quadratische Fehler nur verdoppelt wird. Dem ist jedoch nicht so, da H(f) dann kein Wiener-Filter mehr ist und obige Gleichung auch nicht mehr anwendbar.
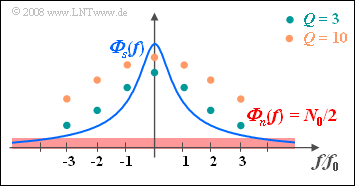
- Die zweite Aussage ist zutreffend, wie aus der folgenden Skizze hervorgeht. Die Punkte markieren den Frequenzgang HWF(f) des Wiener–Kolmogorow–Filters für Q = 3 bzw. für Q = 10. Richtig ist also nur der zweite Lösungsvorschlag.
- Begründung:
- Bei großem Q = 10 werden hohe Anteile weniger gedämpft als bei Q = 3. Deshalb beinhaltet das Filterausgangssignal im Fall <nobr>Q = 10</nobr> mehr höherfrequente Anteile, die auf das Rauschen n(t) zurückgehen.