Aufgaben:Exercise 5.9: Minimization of the MSE

• Return to book

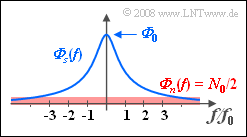
Gegeben ist ein stochastisches Nutzsignal $s(t)$, von dem nur das Leistungsdichtespektrum (LDS) bekannt ist:

$${\it \Phi} _s (f) = \frac{\it{\Phi} _{\rm 0} }{1 + ( {f/f_0 } )^2 }.$$

Dieses LDS ${\it \Phi} _s (f)$ ist in der nebenstehenden Grafik blau dargestellt.

• Die mittlere Leistung von $s(t)$ ergibt sich durch Integration über das Leistungsdichtespektrum:

$$P_s = \int_{ - \infty }^{ + \infty } {{\it \Phi} _s (f)}\, {\rm d} f = {\it \Phi} _0 \cdot f_0 \cdot {\rm{\pi }}.$$

• Additiv überlagert ist dem Nutzsignal $s(t)$ weißes Rauschen mit der Rauschleistungsdichte ${\it \Phi}_n(f) = N_0/2.$
• Als Abkürzung verwenden wir $Q = 2 \cdot {\it \Phi}_0/N_0$, wobei $Q$ als „Qualität” interpretiert werden könnte.
• Zu beachten ist, dass $Q$ kein Signal–zu–Rauschleistungsverhältnis darstellt.

In dieser Aufgabe soll der Frequenzgang$H(f)$ eines Filters ermittelt werden, das den mittleren quadratischen Fehler (MQF) zwischen dem Nutzsignal $s(t)$ und dem Filterausgangssignal $d(t)$ minimiert:

$${\rm{MQF}} = \mathop {\lim }\limits_{T_{\rm M} \to \infty } \frac{1}{T_{\rm M} }\int_{ - T_{\rm M} /2}^{T_{\rm M} /2} {\left| {d(t) - s(t)} \right|^2 \, {\rm{d}}t.}$$

Hinweise:

• Die Aufgabe gehört zum Kapitel Wiener–Kolmogorow–Filter.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Zur Lösung vorgegeben wird das folgende unbestimmte Integral:

$$\int {\frac{1}{a^2 + x^2 }} \, {\rm{d}}x ={1}/{a} \cdot \arctan \left( {{x}/{a}} \right).$$

Fragebogen

1

Welche der folgenden Aussagen sind zutreffend?

	$H(f)$ ist ein Gaußtiefpass.
	$H(f)$ stellt ein Matched–Filter dar.
	$H(f)$ ist ein Wiener–Kolmogorow–Filter.

2

Bestimmen Sie den Frequenzgang $H(f)$ des hierfür optimalen Filters. Welche Werte ergeben sich mit $Q = 3$ bei $f = 0$ und $f = 2f_0$?

$H(f = 0) \ = $

$H(f = 2f_0)\ = $

3

Es gelte weiter $Q = 3$. Berechnen Sie den mittleren quadratischen Fehler ($\rm MQF$) bezogen auf $P_s$ für das bestmögliche Filter.

${\rm MQF}/P_s \ = $

4

Wie groß muss der „Qualitätsfaktor” $Q$ mindestens gewählt werden, damit für den Quotienten der Wert ${\rm MQF}/P_s = 0.1$ erreicht werden kann?

$Q_\text{min} \ = $

5

Welche der folgenden Aussagen sind zutreffend?

	Ein formgleiches Filter $H(f) = K \cdot H_{\rm WF}(f)$ führt zum gleichen Ergebnis.
	Das Ausgangssignal $d(t)$ enthält bei größerem $Q$ mehr höherfrequente Anteile.

Musterlösung

Solution

(1)  Richtig ist hier nur der letzte Lösungsvorschlag:

• Die Aufgabenstellung („Minimierung des mittleren quadratischen Fehlers”) weist bereits auf das Filter nach Wiener–Kolmogorow hin.
• Das Matched–Filter verwendet man dagegen, um die Signalenergie zu bündeln und dadurch für einen vorgegebenen Zeitpunkt das S/N–Verhältnis zu maximieren.

(2)  Für den optimalen Frequenzgang gilt nach Wiener und Kolmogorow allgemein:

$$H(f) = H_{\rm WF} (f) = \frac{1}{{1 + {\it \Phi} _n (f)/{\it \Phi} _s (f)}}.$$

Mit den gegebenen Leistungsdichtespektren kann hierfür auch geschrieben werden:

$$H(f) = \frac{1}{{1 + {N_0 }/({{2{\it \Phi} _0 })}\cdot \left[ {1 + ( {f/f_0 } )^2 } \right]}} = \frac{1}{{1 + {1}/{Q}\cdot \left[ {1 + ( {f/f_0 } )^2 } \right]}}.$$

Mit $Q = 3$ folgt daraus:

$$H( {f = 0} ) = \frac{1}{{1 + {1}/{Q}}} = \frac{Q}{Q + 1} \hspace{0.15cm}\underline {= 0.75},$$

$$H( {f = 2f_0 } ) = \frac{1}{{1 + {5}/{Q}}} = \frac{Q}{Q + 5} \hspace{0.15cm}\underline {= 0.375}.$$

(3)  Für das in der Teilaufgabe (2) berechnete Filter gilt unter Berücksichtigung der Symmetrie:

$${\rm{MQF = }}\int_{-\infty}^{+\infty} H(f) \cdot {\it \Phi} _n (f) \,\, {\rm{d}}f = \int_{0}^{+\infty} \frac{N_0}{{1 + {N_0 }/({{2{\it \Phi} _0 })}\cdot \left[ {1 + ( {f/f_0 } )^2 } \right]}} \,\, {\rm{d}}f .$$

Hierfür kann mit $Q = 2 \cdot {\it \Phi}_0/N_0$ und $a^2 = Q + 1$ auch geschrieben werden:

$${\rm{MQF = }}\int_0^\infty {\frac{{2{\it \Phi} _0 }}{{ Q+1 + ( {f/f_0 })^2 }}} \,\, {\rm{d}}f = 2{\it \Phi} _0 \cdot f_0 \int_0^\infty {\frac{1}{a^2 + x^2 }}\,\, {\rm{d}}x.$$

Mit dem angegebenen Integral führt dies zum Ergebnis:

$${\rm{MQF}} = \frac{{2{\it \Phi} _0 f_0 }}{{\sqrt {1 + Q} }}\left( {\arctan ( \infty ) - \arctan ( 0 )} \right) = \frac{{{\it \Phi} _0 f_0 {\rm{\pi }}}}{{\sqrt {1 + Q} }}.$$

Normiert man MQF auf die Nutzleistung $P_s$, so erhält man für $Q=3$:

$$\frac{\rm{MQF}}{P_s} = \frac{1}{{\sqrt {1 + Q} }} \hspace{0.15cm}\underline { = 0.5}.$$

(4)  Aus der Berechnung in in der Teilaufgabe (3) folgt für ${\rm MQF}/P_s \ge 0.1$ direkt die Bedingung $Q \ge 99$   ⇒   $Q_{\rm min} \hspace{0.15cm}\underline{= 99}$. Je größer $Q$ ist, desto kleiner wird der mittlere quadratische Fehler.

(5)  Richtig ist nur der zweite Lösungsvorschlag:

• Ein zum Wiener–Kolmogorow–Filterr formgleicher Frequenzgang  ⇒  $H(f) = K \cdot H_{\rm WF}(f)$ mit $K \ne 1$ führt stets zu großen Verfälschungen. Dies kann man sich zum Beispiel am rauschfreien Fall ($Q \to \infty$) verdeutlichen:
• In diesem Fall wäre $d(t) = K \cdot s(t)$ und die Optimierungsaufgabe trotz guter Bedingungen extrem schlecht gelöst.
• Aus der Gleichung

$${\rm{MQF}} = \int_{ - \infty }^{ + \infty } {H_{\rm WF} (f)} \cdot \it{\Phi} _n (f)\,\,{\rm{d}}f$$

könnte man fälschlicherweise schließen, dass durch ein Filter $H(f) = 2 \cdot H_{\rm WF}(f))$ der mittlere quadratische Fehler nur verdoppelt wird. Dem ist jedoch nicht so, da $H(f)$dann kein Wiener-Filter mehr ist und obige Gleichung auch nicht mehr anwendbar.

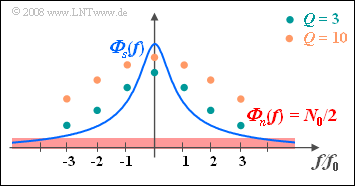
Die zweite Aussage ist zutreffend, wie aus der nebenstehenden Skizze hervorgeht.

• Die Punkte markieren den Frequenzgang $H_{\rm WF}(f))$ des Wiener–Kolmogorow–Filters für $Q = 3$ bzw. für $Q = 10$.
• Bei größerem $Q (= 10)$ werden hohe Anteile weniger gedämpft als bei niedrigerem $Q (= 3)$.
• Deshalb beinhaltet das Filterausgangssignal im Fall $Q = 10$ auch mehr höherfrequente Anteile, die auf das Rauschen $n(t)$ zurückgehen.