Aufgaben:Exercise 1.4Z: Entropy of the AMI Code

• Return to book

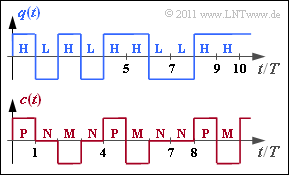
Wir gehen von ähnlichen Voraussetzungen wie in der Aufgabe 1.4 aus: Eine Binärquelle liefert die Quellensybolfolge $\langle q_\nu \rangle$ mit $q_\nu \in \{ {\rm L}, {\rm H} \}$, wobei es keine statistischen Bindungen zwischen den einzelnen Folgenelementen gibt.

Für die Symbolwahrscheinlichkeiten gelte:

• $p_{\rm L} =p_{\rm H} = 1/2$ (in den Teilaufgaben 1 und 2),
• $p_{\rm L} = 1/4, \, p_{\rm H} = 3/4$ (Teilaufgaben 3, 4 und 5),
• $p_{\rm L} = 3/4, \, p_{\rm H} = 1/4$ (Teilaufgabe 6).

Das dargestellte Codersignal $c(t)$ und die zugehörige Symbolfolge $\langle c_\nu \rangle$ mit $c_\nu \in \{{\rm P}, {\rm N}, {\rm M} \}$ ergibt sich aus der AMI–Codierung (Alternate Mark Inversion) nach folgender Vorschrift:

• Das Binärsymbol $\rm L$  ⇒  Low wird stets durch das Ternärsymbol $\rm N$  ⇒  Null dargestellt.
• Das Binärsymbol $\rm H$  ⇒  High wird ebenfalls deterministisch, aber alternierend (daher der Name „AMI”) durch die Symbole $\rm P$  ⇒  Plus und $\rm M$  ⇒  Minus codiert.

In dieser Aufgabe sollen für die drei oben genannten Parametersätze der Entscheidungsgehalt $H_0$ sowie die resultierende Entropie $H_{\rm C}$ der Codesymbolfolge $\langle c_\nu \rangle$ bestimmt werden. Die relative Redundanz der Codefolge ergibt sich daraus entsprechend der Gleichung

$$r_{\rm C} = \frac{H_{\rm 0}-H_{\rm C}}{H_{\rm C}} \hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel Nachrichtenquellen mit Gedächtnis.
• Bezug genommen wird insbesondere auf die Seite Die Entropie des AMI-Codes.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Allgemein bestehen folgende Relationen zwischen dem Entscheidungsgehalt $H_0$, der Entropie $H$ (hier gleich $H_{\rm C}$ und den Entropienäherungen:   $H \le$ ...$\le H_3 \le H_2 \le H_1 \le H_0 \hspace{0.05cm}.$
• In Aufgabe 1.4 wurden für gleichwahrscheinliche Symbole $\rm L$ und $\rm H$ die Entropie–Näherungen wie folgt berechnet (jeweils in „bit/Symbol”):   $H_1 = 1.500\hspace{0.05cm},\hspace{0.2cm} H_2 = 1.375\hspace{0.05cm},\hspace{0.2cm}H_3 = 1.292 \hspace{0.05cm}.$

Fragebogen

1

Die Quellensymbole seien gleichwahrscheinlich. Wie groß ist die Entropie $H_{\rm C}$ der Codesymbolfolge $\langle c_\nu \rangle$?

$p_{\rm L} = 1/2, \ p_{\rm H}= 1/2$:    $H_{\rm C} \ =$ $\ \rm bit/Ternärsymbol$

2

Wie groß ist die relative Redundanz der Codesymbolfolge?

$p_{\rm L} = 1/2, \ p_{\rm H}= 1/2$:   $r_{\rm C} \ =$ $\ \rm \%$

3

Für die Binärquelle gelte nun $p_{\rm L} = 1/4$ und $p_{\rm H} = 3/4$. Welcher Wert ergibt sich nun für die Entropie der Codesymbolfolge?

$p_{\rm L} = 1/4, \ p_{\rm H}= 3/4$:   $H_{\rm C} \ =$ $\ \rm bit/Ternärsymbol$

4

Wie groß ist nun die relative Redundanz der Codesymbolfolge?

$p_{\rm L} = 1/4, \ p_{\rm H} = 3/4$:   $r_{\rm C} \ =$ $\ \rm \%$

5

Berechnen Sie die Näherung $H_{\rm 1}$ der Coderentropie für $p_{\rm L} = 1/4, \ p_{\rm H} = 3/4$.

$p_{\rm L} = 1/4, \ p_{\rm H} = 3/4$:   $H_{\rm 1} \ =$ $\ \rm bit/Ternärsymbol$

6

Berechnen Sie die Näherung $H_{\rm 1}$ der Coderentropie für $p_{\rm L} = 3/4, \ p_{\rm H} = 1/4$.

$p_{\rm L} = 3/4, \ p_{\rm H} = 1/4$:   $H_{\rm 1} \ =$ $\ \rm bit/Ternärsymbol$

Musterlösung

Solution

(1)  Da durch den AMI–Code weder neue Information hinzukommt noch Information verschwindet, ist die Entropie $H_{\rm C}$ der Codesymbolfolge $\langle c_\nu \rangle$ gleich der Quellenentropie $H_{\rm Q}$. Bei gleichwahrscheinlichen und statistisch voneinander unabhängigen Quellensymbolen gilt deshalb:

$$H_{\rm Q} {= 1 \,{\rm bit/Bin\ddot{a}rsymbol}} \hspace{0.3cm} \Rightarrow\hspace{0.3cm} H_{\rm C} \hspace{0.15cm} \underline {= 1 \,{\rm bit/Tern\ddot{a}rsymbol}} \hspace{0.05cm}.$$

(2)  Der Entscheidungsgehalt einer ternären Quelle beträgt $H_0 = \log_2 \; (3) = 1.585\; \rm bit/Symbol$. Damit ergibt sich für die relative Redundanz

$$r_{\rm C} =1 -{H_{\rm C}/H_{\rm 0}}=1-1/{\rm log}_2\hspace{0.05cm}(3) \hspace{0.15cm} \underline {= 36.9 \,\%} \hspace{0.05cm}.$$

(3)  Es gilt weiter $H_{\rm C} = H_{\rm Q}$. Wegen den ungleichen Symbolwahrscheinlichkeiten ist aber nun $H_{\rm Q}$ kleiner:

$$H_{\rm Q} = \frac{1}{4} \cdot {\rm log}_2\hspace{0.05cm} (4) + \frac{3}{4} \cdot {\rm log}_2\hspace{0.1cm} (4/3) {= 0.811 \,{\rm bit/Bin\ddot{a}rsymbol}} \hspace{0.3cm} \Rightarrow\hspace{0.3cm} H_{\rm C} = H_{\rm Q} \hspace{0.15cm} \underline {= 0.811 \,{\rm bit/Tern\ddot{a}rsymbol}} \hspace{0.05cm}.$$

(4)  In Analogie zur Teilaufgabe (2) gilt nun $r_{\rm C} = 1 - 0.811/1.585 \hspace{0.15cm} \underline {= 48.8 \,\%} \hspace{0.05cm}.$ Man kann dieses Ergebnis verallgemeinern. Es gilt nämlich :

$$(1-0.488) = (1- 0.189) \cdot (1- 0.369)\hspace{0.3cm} \Rightarrow\hspace{0.3cm} (1-r_{\rm Codefolge}) = (1-r_{\rm Quelle}) \cdot (1- r_{\rm AMI-Code}) \hspace{0.05cm}.$$

(5)  Da jedes $\rm L$ auf $\rm N$ abgebildet wird und $\rm H$ alternierend auf $\rm M$ und $\rm P$, gilt

$$p_{\rm N} = p_{\rm L} = 1/4\hspace{0.05cm},\hspace{0.2cm}p_{\rm P} = p_{\rm M} = p_{\rm H}/2 = 3/8\hspace{0.3cm} \Rightarrow\hspace{0.3cm} H_1 = {1}/{4} \cdot {\rm log}_2\hspace{0.1cm} (4) + 2 \cdot {3}/{8} \cdot {\rm log}_2\hspace{0.1cm}(8/3) \hspace{0.15cm} \underline {= 1.56 \,{\rm bit/Tern\ddot{a}rsymbol}} \hspace{0.05cm}.$$

(6)  Nun ergeben sich die Auftrittswahrscheinlichkeiten der Ternärsymbole zu $p_{\rm N} = 3/4$ sowie $p_{\rm P} = p_{\rm M} =1/8$. Somit gilt:

$$H_1 = {3}/{4} \cdot {\rm log}_2\hspace{0.1cm} (4/3) + 2 \cdot {1}/{8} \cdot {\rm log}_2\hspace{0.1cm}(8) \hspace{0.15cm} \underline {= 1.06 \,{\rm bit/Tern\ddot{a}rsymbol}} \hspace{0.05cm}.$$

Interpretation:

• Für $p_{\rm L} = 1/4, \ p_{\rm H} = 3/4$ ergibt sich $H_1 = 1.56 \; \rm bit/Symbol$.
• Für $p_{\rm L} = 3/4, \ p_{\rm H} = 1/4$ ergibt sich dagegen mit $H_1 = 1.06 \; \rm bit/Symbol$ ein deutlich kleinerer Wert.
• Für beide Parameterkombinationen gilt aber gleichermaßen:

$$H_0 = 1.585 \,{\rm bit/Symbol}\hspace{0.05cm},\hspace{0.2cm}H_{\rm C} = \lim_{k \rightarrow \infty } H_k = 0.811 \,{\rm bit/Symbol} \hspace{0.05cm}.$$

Daraus folgt:
Betrachtet man zwei Nachrichtenquellen Q1 und Q2 mit gleichem Symbolumfang $M$  ⇒  Entscheidungsgehalt  $H_0 = \rm const.$, wobei bei der Quelle Q1 die Entropienäherung erster Ordnung $(H_1)$ deutlich größer ist als bei der Quelle Q2, so kann man daraus noch lange nicht schließen, dass die Entropie von Q1 tatsächlich größer ist als die Entropie von Q2. Vielmehr muss man für beide Quellen

• genügend viele Entropienäherungen $H_1$, $H_2$, $H_3$, ... berechnen, und
• daraus (grafisch oder analytisch) den Grenzwert von $H_k$ für $k \to \infty$ bestimmen.

Erst dann ist eine endgültige Aussage über die Entropieverhältnisse möglich.