Difference between revisions of "Aufgaben:Exercise 2.11Z: Arithmetic Coding once again"
m (Guenter verschob die Seite 2.12 Nochmals Arithmetische Codierung nach 2.11Z Nochmals Arithmetische Codierung) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID2473__Inf_A_2_12.png|right|]] | + | [[File:P_ID2473__Inf_A_2_12.png|right|Intervallbereiche für die Arithmetische Codierung]] |
| − | Wir betrachten hier die arithmetische Codierung (AC). Alle notwendigen Informationen zu dieser Art von Entropiecodierung finden Sie in der Aufgabe | + | Wir betrachten hier die arithmetische Codierung (AC). Alle notwendigen Informationen zu dieser Art von Entropiecodierung finden Sie in der [[Aufgaben:2.11_Arithmetische_Codierung|Aufgabe 2.11]]. |
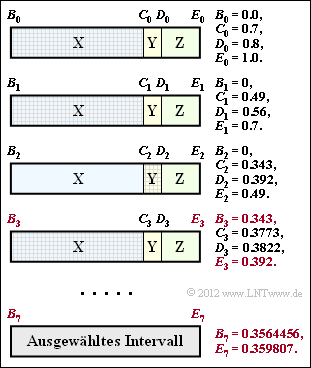
| − | Auch | + | Auch die Grafik ist das Ergebnis von Aufgabe 2.11. Die für die aktuelle Aufgabe wichtigen Zahlenwerte für die Codierschritte 3 und 7 sind farblich hervorgehoben: |
| − | + | * Das Intervall für $N= 3$ (Symbolfolge <b>XXY</b>) beginnt bei $B_3 = 0.343$ und reicht bis zum Endwert $E_3 = 0.392$. | |
| − | + | * Das Intervall für $N= 7$ (Symbolfolge <b>XXYXXXZ</b>) beginnt bei $B_7 = 0.3564456$ und endet bei $E_7 =0.359807$. | |
| − | |||
| − | |||
In dieser Aufgabe geht es nur um die Zuweisung von Binärfolgen zu den ausgewählten Intervallen. Man geht wie folgt vor: | In dieser Aufgabe geht es nur um die Zuweisung von Binärfolgen zu den ausgewählten Intervallen. Man geht wie folgt vor: | ||
| − | + | * Das Intervall $I$ wird bestimmt durch den Beginn $B$, das Ende $E$, die Intervallbreite ${\it \Delta} = E-B$ sowie die Intervallmitte $M = (B+E)/2$. | |
| + | * Das Intervall $I$ wird gekennzeichnet durch die Binärdarstellung (mit begrenzter Auflösung) eines beliebigen reellen Zahlenwertes $r \in I$ . Beispielsweise wählt man $r \approx M$. | ||
| + | * Die erforderliche Bitanzahl ergibt sich aus der Intervallbreite nach folgender Gleichung (die nach unten offenen Klammern bedeuten „nach oben runden”): | ||
| + | :$$N_{\rm Bit} = \left\lceil{\rm log_2} \hspace{0.15cm} 1/{\it \Delta} \right\rceil+1\hspace{0.05cm}. $$ | ||
| − | + | Beispielsweise steht für $N_{\rm Bit} = 5$ der Binärcode <b>01001</b> für die folgende reellwertige Zahl <i>r</i>: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
:$$r = 0 \cdot 2^{-1}+1 \cdot 2^{-2}+0 \cdot 2^{-3}+0 \cdot 2^{-4}+1 \cdot 2^{-5} = 0.28125 | :$$r = 0 \cdot 2^{-1}+1 \cdot 2^{-2}+0 \cdot 2^{-3}+0 \cdot 2^{-4}+1 \cdot 2^{-5} = 0.28125 | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| Line 28: | Line 24: | ||
*Die Aufgabe gehört zum Kapitel [[Informationstheorie/Weitere_Quellencodierverfahren|Weitere Quellencodierverfahren]]. | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Weitere_Quellencodierverfahren|Weitere Quellencodierverfahren]]. | ||
*Insbesondere wird Bezug genommen auf die Seite [[Informationstheorie/Weitere_Quellencodierverfahren#Arithmetische_Codierung|Arithmetische Codierung]]. | *Insbesondere wird Bezug genommen auf die Seite [[Informationstheorie/Weitere_Quellencodierverfahren#Arithmetische_Codierung|Arithmetische Codierung]]. | ||
| − | * | + | *Weitere Informationen zum Thema finden Sie auch in diesem [https://de.wikipedia.org/wiki/Arithmetisches_Kodieren WIKIPEDIA-Artikel] |
*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| − | |||
| − | |||
| Line 37: | Line 31: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie viele Bit werden zur Darstellung der | + | {Wie viele Bit werden zur Darstellung der Quellensymbolfolge <b>XXY</b> ⇒ $N = 3$ benutzt? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $N_\text{Bit} \ = \ $ { 6 } |
| Line 49: | Line 43: | ||
| − | {Wie viele Bit werden zur Darstellung | + | {Wie viele Bit werden zur Darstellung der Quellensymbolfolge <b>XXYXXXZ</b> ⇒ $N = 7$ benutzt? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $N_\text{Bit} \ = \ $ { 11 } |
| − | {Ist <b>01011100001</b> ein gültiger Code für die | + | {Ist <b>01011100001</b> ein gültiger Code für die Quellensymbolfolge <b>XXYXXXZ</b>? |
|type="[]"} | |type="[]"} | ||
- Ja. | - Ja. | ||
| Line 63: | Line 57: | ||
|type="[]"} | |type="[]"} | ||
+ Es handelt sich um eine gemeinsame Codierung ganzer Folgen. | + Es handelt sich um eine gemeinsame Codierung ganzer Folgen. | ||
| − | + Eine 32 Bit–Rechnerarchitektur begrenzt die Folgenlänge | + | + Eine 32 Bit–Rechnerarchitektur begrenzt die Folgenlänge $N$. |
+ Dieses Problem lässt sich durch Integer–Realisierung umgehen. | + Dieses Problem lässt sich durch Integer–Realisierung umgehen. | ||
+ Eine Integer–Realisierung erhöht die Codiergeschwindigkeit. | + Eine Integer–Realisierung erhöht die Codiergeschwindigkeit. | ||
Revision as of 14:48, 27 May 2017
Wir betrachten hier die arithmetische Codierung (AC). Alle notwendigen Informationen zu dieser Art von Entropiecodierung finden Sie in der Aufgabe 2.11.
Auch die Grafik ist das Ergebnis von Aufgabe 2.11. Die für die aktuelle Aufgabe wichtigen Zahlenwerte für die Codierschritte 3 und 7 sind farblich hervorgehoben:
- Das Intervall für $N= 3$ (Symbolfolge XXY) beginnt bei $B_3 = 0.343$ und reicht bis zum Endwert $E_3 = 0.392$.
- Das Intervall für $N= 7$ (Symbolfolge XXYXXXZ) beginnt bei $B_7 = 0.3564456$ und endet bei $E_7 =0.359807$.
In dieser Aufgabe geht es nur um die Zuweisung von Binärfolgen zu den ausgewählten Intervallen. Man geht wie folgt vor:
- Das Intervall $I$ wird bestimmt durch den Beginn $B$, das Ende $E$, die Intervallbreite ${\it \Delta} = E-B$ sowie die Intervallmitte $M = (B+E)/2$.
- Das Intervall $I$ wird gekennzeichnet durch die Binärdarstellung (mit begrenzter Auflösung) eines beliebigen reellen Zahlenwertes $r \in I$ . Beispielsweise wählt man $r \approx M$.
- Die erforderliche Bitanzahl ergibt sich aus der Intervallbreite nach folgender Gleichung (die nach unten offenen Klammern bedeuten „nach oben runden”):
- $$N_{\rm Bit} = \left\lceil{\rm log_2} \hspace{0.15cm} 1/{\it \Delta} \right\rceil+1\hspace{0.05cm}. $$
Beispielsweise steht für $N_{\rm Bit} = 5$ der Binärcode 01001 für die folgende reellwertige Zahl r:
- $$r = 0 \cdot 2^{-1}+1 \cdot 2^{-2}+0 \cdot 2^{-3}+0 \cdot 2^{-4}+1 \cdot 2^{-5} = 0.28125 \hspace{0.05cm}. $$
Hinweise:
- Die Aufgabe gehört zum Kapitel Weitere Quellencodierverfahren.
- Insbesondere wird Bezug genommen auf die Seite Arithmetische Codierung.
- Weitere Informationen zum Thema finden Sie auch in diesem WIKIPEDIA-Artikel
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
- $$N_{\rm Bit} = {\rm ld} \hspace{0.15cm} \left\lceil \frac{1}{0.049}\right\rceil+1\hspace{0.15cm}\underline{= 6} \hspace{0.05cm}.$$
2. Das ausgewählte Intervall ergibt sich zu I = [0.343, 0.392). Die Mitte liegt bei M3 = 0.3675. Zur Bestimmung des arithmetischen Codes versuchen wir, die Intervallmitte durch eine Binärdarstellung möglichst gut zu erreichen. Da uns gerade kein entsprechendes Tool zur Lösung dieser Aufgabe zur Verfügung steht, gehen wir von folgenden Nebenrechnungen aus:
- H4 = 2–2 + 2–4 = 0.3125 ⇒ gehört nicht zum Intervall I,
- H5 = H4 + 2–5 = 0.34375 ∈ I ⇒ Binärdarstellung: 0.01011 ⇒ Code: 01011.
- H6 = H5 + 2–6 = 0.359375 ∈ I ⇒ Binärdarstellung: 0.010111 ⇒ Code: 010111.
- H7 = H6 + 2–7 = 0.3671875 ∈ I ⇒ Binärdarstellung: 0.0101111 ⇒ Code: 0101111.
- H12 = H7 + 2–12 = 0.3674316406 ∈ I ⇒ binär: 0.010111100001 ⇒ Code: 010111100001.
Der entsprechende 6 Bit–Code lautet somit AC = 010111 ⇒ Richtig ist der Vorschlag 2.
3. Hier ergibt sich mit dem Beginn B7 = 0.3564456 und dem Ende E7 = 0.359807 die Intervallbreite Δ7 = 0.0033614 und damit
- $$N_{\rm Bit} = \left\lceil {\rm ld} \hspace{0.15cm} \frac{1}{0.0033614} \right\rceil + 1\hspace{0.15cm} = \left\lceil {\rm ld} \hspace{0.15cm} 297.5 \right\rceil + 1\hspace{0.15cm} \underline{= 11} \hspace{0.05cm}.$$
4. Die Binärdarstellung des Codes 01011100001 ergibt
- $$2^{-2}+ 2^{-4}+ 2^{-5}+ 2^{-6}+ 2^{-11} = 0.3598632813 > E_7 \hspace{0.05cm}.$$
Richtig ist also NEIN. Wegen
- $$2^{-2}+ 2^{-4}+ 2^{-5}+ 2^{-7}+ 2^{-8}+ 2^{-9}+ 2^{-11} =0.3579101563$$
- $$\Rightarrow \hspace{0.3cm} B_7 \le 0.3579101563 < E_7$$
ist der gültige arithmetische Code gleich 01011011101.
e) Alle Aussagen sind richtig. Sie können sich davon beispielsweise in [BCK02] überzeugen.