Difference between revisions of "Aufgaben:Exercise 3.4: Entropy for Different PMF"
| Line 45: | Line 45: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Mit $P_X(X) = [ 0.1, 0.2, 0.3, 0.4]$ erhält man für die Entropie: |
| − | + | :$$H_{\rm a}(X) = | |
| − | $$H_{\rm a}(X) = | ||
0.1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + | 0.1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + | ||
0.2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.2} + | 0.2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.2} + | ||
0.3 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.3} + | 0.3 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.3} + | ||
0.4 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.4} | 0.4 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.4} | ||
| − | \hspace{0.15cm} \underline {= 1.846} \hspace{0.05cm}$$ | + | \hspace{0.15cm} \underline {= 1.846} \hspace{0.05cm}.$$ |
| − | |||
Hier (und bei den anderen Aufgaben) ist jeweils die Pseudo–Einheit „bit” anzufügen. | Hier (und bei den anderen Aufgaben) ist jeweils die Pseudo–Einheit „bit” anzufügen. | ||
| − | '''2 | + | '''(2)''' Die Entropie $H_{\rm b}(X)$ lässt sich als Summe zweier Anteile $H_{\rm b1}(X)$ und $H_{\rm b2}(X)$ darstellen, mit: |
| − | + | :$$H_{\rm b1}(X) = | |
| − | $$H_{\rm b1}(X) = | ||
0.1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + | 0.1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + | ||
| − | 0.2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.2} = 0.797 \hspace{0.05cm}$$ | + | 0.2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.2} = 0.797 \hspace{0.05cm},$$ |
| − | + | :$$H_{\rm b2}(X) = | |
| − | $$H_{\rm b2}(X) = | ||
p_3 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_3} + | p_3 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_3} + | ||
| − | (0.7-p_3) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.7-p_3} \hspace{0.05cm}$$ | + | (0.7-p_3) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.7-p_3} \hspace{0.05cm}.$$ |
| − | Die zweite Funktion ist für $ | + | Die zweite Funktion ist maximal für $p_3 = p_4 = 0.35$. Ein ähnlicher Zusammenhang hat sich bei der binären Entropiefunktion ergeben. Damit erhält man: |
| − | $$H_{\rm b2}(X) = 2 \cdot | + | :$$H_{\rm b2}(X) = 2 \cdot |
p_3 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_3} = | p_3 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_3} = | ||
0.7 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.35} = 1.060$$ | 0.7 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.35} = 1.060$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} H_{\rm b}(X) = H_{\rm b1}(X) + H_{\rm b2}(X) = 0.797 + 1.060 \hspace{0.15cm} \underline {= 1.857} \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | $$H_{\rm c}(X) = | + | '''(3)''' Analog zur Teilaufgabe (2) ergibt sich mit $p_1 = 0.1$, $p_4 = 0.4$ das Maximum für $p_2 = p_3 = p_3 = 0.25$: |
| + | :$$H_{\rm c}(X) = | ||
0.1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + | 0.1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + | ||
2 \cdot 0.25 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.25} + | 2 \cdot 0.25 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.25} + | ||
0.4 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.4} | 0.4 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.4} | ||
| − | \hspace{0.15cm} \underline {= 1.861} \hspace{0.05cm}$$ | + | \hspace{0.15cm} \underline {= 1.861} \hspace{0.05cm}.$$ |
| − | |||
| − | |||
| − | $$H_{\rm max}(X) = | + | '''(4)''' Die maximale Entropie für den Symbolumfang $M=4$ ergibt sich bei gleichen Wahrscheinlichkeiten ( $p_1 = p_2 = p_3 = p_4 = 0.25$): |
| + | :$$H_{\rm max}(X) = | ||
{\rm log}_2 \hspace{0.1cm} M | {\rm log}_2 \hspace{0.1cm} M | ||
| − | \hspace{0.15cm} \underline {= 2} \hspace{0.05cm} | + | \hspace{0.15cm} \underline {= 2} \hspace{0.05cm}.$$ |
| − | |||
| − | |||
| − | $$\Delta H(X) = 1- | + | Die Differenz der Entropien entsprechend (4) und (3) ergibt ${\it \Delta} H(X) = 0.139 \ \rm bit$. Hierbei gilt: |
| + | :$${\it \Delta} H(X) = 1- | ||
0.1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} - | 0.1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} - | ||
0.4 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.4} | 0.4 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.4} | ||
| − | \hspace{0.05cm}$$ | + | \hspace{0.05cm}.$$ |
Mit der binären Entropiefunktion | Mit der binären Entropiefunktion | ||
| Line 105: | Line 97: | ||
lässt sich hierfür auch schreiben: | lässt sich hierfür auch schreiben: | ||
| − | $$\Delta H(X) = 0.5 \cdot \left [ 1- H_{\rm bin}(0.2) \right ] = | + | $${\it \Delta} H(X) = 0.5 \cdot \left [ 1- H_{\rm bin}(0.2) \right ] = |
0.5 \cdot \left [ 1- 0.722 \right ] = 0.139 | 0.5 \cdot \left [ 1- 0.722 \right ] = 0.139 | ||
| − | \hspace{0.05cm}$$ | + | \hspace{0.05cm}.$$ |
Revision as of 14:18, 30 May 2017
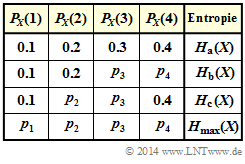
In der ersten Zeile der nebenstehenden Tabelle ist die im Folgenden die mit „a” bezeichnete Wahrscheinlichkeitsfunktion angegeben. Für diese PMF $P_X(X) = [0.1, 0.2, 0.3, 0.4 ]$ soll soll in der Teilaufgabe (1) die Entropie berechnet werden:
- $$H_{\rm a}(X) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{X}(X)}\right ]= - {\rm E} \left [ {\rm log}_2 \hspace{0.1cm}{P_{X}(X)}\right ].$$
Da hier der Logarithmus zur Basis 2 verwendet wird, ist die Pseudo–Einheit „bit” anzufügen.
In den weiteren Aufgaben sollen jeweils einige Wahrscheinlichkeiten variiert werden und zwar derart, dass sich jeweils die größtmögliche Entropie ergibt:
- Durch geeignete Variation von $p_3$ und $p_4$ kommt man zur maximalen Entropie $H_{\rm b}(X)$ unter der Voraussetzung $p_1 = 0.1$ und $p_2 = 0.2$ ⇒ Teilaufgabe (2).
- Durch geeignete Variation von $p_2$ und $p_3$ kommt man zur maximalen Entropie $H_{\rm c}(X)$ unter der Voraussetzung $p_1 = 0.1$ und $p_4 = 0.4$ ⇒ Teilaufgabe (3).
- In der Teilaufgabe (4) sind alle vier Parameter zur Variation freigegeben, die entsprechend der maximalen Entropie ⇒ $H_{\rm max}(X)$ zu bestimmen sind.
Hinweise:
- Die Aufgabe gehört zum Kapitel Einige Vorbemerkungen zu den 2D-Zufallsgrößen.
- Insbesondere wird Bezug genommen auf die Seite Wahrscheinlichkeitsfunktion undEntropie.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
- $$H_{\rm a}(X) = 0.1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + 0.2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.2} + 0.3 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.3} + 0.4 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.4} \hspace{0.15cm} \underline {= 1.846} \hspace{0.05cm}.$$
Hier (und bei den anderen Aufgaben) ist jeweils die Pseudo–Einheit „bit” anzufügen.
(2) Die Entropie $H_{\rm b}(X)$ lässt sich als Summe zweier Anteile $H_{\rm b1}(X)$ und $H_{\rm b2}(X)$ darstellen, mit:
- $$H_{\rm b1}(X) = 0.1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + 0.2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.2} = 0.797 \hspace{0.05cm},$$
- $$H_{\rm b2}(X) = p_3 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_3} + (0.7-p_3) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.7-p_3} \hspace{0.05cm}.$$
Die zweite Funktion ist maximal für $p_3 = p_4 = 0.35$. Ein ähnlicher Zusammenhang hat sich bei der binären Entropiefunktion ergeben. Damit erhält man:
- $$H_{\rm b2}(X) = 2 \cdot p_3 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_3} = 0.7 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.35} = 1.060$$
- $$\Rightarrow \hspace{0.3cm} H_{\rm b}(X) = H_{\rm b1}(X) + H_{\rm b2}(X) = 0.797 + 1.060 \hspace{0.15cm} \underline {= 1.857} \hspace{0.05cm}.$$
(3) Analog zur Teilaufgabe (2) ergibt sich mit $p_1 = 0.1$, $p_4 = 0.4$ das Maximum für $p_2 = p_3 = p_3 = 0.25$:
- $$H_{\rm c}(X) = 0.1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + 2 \cdot 0.25 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.25} + 0.4 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.4} \hspace{0.15cm} \underline {= 1.861} \hspace{0.05cm}.$$
(4) Die maximale Entropie für den Symbolumfang $M=4$ ergibt sich bei gleichen Wahrscheinlichkeiten ( $p_1 = p_2 = p_3 = p_4 = 0.25$):
- $$H_{\rm max}(X) = {\rm log}_2 \hspace{0.1cm} M \hspace{0.15cm} \underline {= 2} \hspace{0.05cm}.$$
Die Differenz der Entropien entsprechend (4) und (3) ergibt ${\it \Delta} H(X) = 0.139 \ \rm bit$. Hierbei gilt:
- $${\it \Delta} H(X) = 1- 0.1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} - 0.4 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.4} \hspace{0.05cm}.$$
Mit der binären Entropiefunktion
$$H_{\rm bin}(p) = p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p} + (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p}$$
lässt sich hierfür auch schreiben:
$${\it \Delta} H(X) = 0.5 \cdot \left [ 1- H_{\rm bin}(0.2) \right ] = 0.5 \cdot \left [ 1- 0.722 \right ] = 0.139 \hspace{0.05cm}.$$