Difference between revisions of "Aufgaben:Exercise 4.3Z: Exponential and Laplace Distribution"
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID2875__Inf_Z_4_3.png|right|frame|WDF | + | [[File:P_ID2875__Inf_Z_4_3.png|right|frame|WDF von Exponential– und Laplaceverteilung]] |
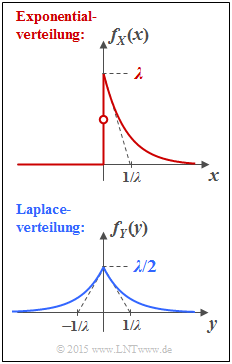
Wir betrachten hier die Wahrscheinlichkeitsdichtefunktionen (WDF) zweier wertkontinuierlicher Zufallsgrößen: | Wir betrachten hier die Wahrscheinlichkeitsdichtefunktionen (WDF) zweier wertkontinuierlicher Zufallsgrößen: | ||
* Die Zufallsgröße $X$ ist exponentialverteilt (siehe obere Darstellung): Für $x<0$ ist $f_X(x) = 0$, und für positive $x$–Werte gilt: | * Die Zufallsgröße $X$ ist exponentialverteilt (siehe obere Darstellung): Für $x<0$ ist $f_X(x) = 0$, und für positive $x$–Werte gilt: | ||
| Line 37: | Line 37: | ||
{Berechnen Sie die differentielle Entropie der Exponentialverteilung für $\lambda = 1$. | {Berechnen Sie die differentielle Entropie der Exponentialverteilung für $\lambda = 1$. | ||
|type="{}"} | |type="{}"} | ||
| − | $h(X) \ = \ $ { 1.443 3% } | + | $h(X) \ = \ $ { 1.443 3% } $\ \rm bit$ |
| − | {Welche Kenngröße ${\it \Gamma}_{\hspace{-0.05cm} \rm L} $ ergibt sich für die Exponentialverteilung entsprechend der Form $h(X) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ({\it \Gamma}_{\hspace{-0.05cm} \rm L} \cdot \sigma^2)$ ? | + | {Welche Kenngröße ${\it \Gamma}_{{\hspace{-0.05cm} \rm L}, \hspace{0.05cm}(X)} $ ergibt sich für die Exponentialverteilung entsprechend der Form $h(X) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ({\it \Gamma}_{\hspace{-0.05cm} \rm L} \cdot \sigma^2)$ ? |
|type="{}"} | |type="{}"} | ||
${\it \Gamma}_{{\hspace{-0.05cm} \rm L}, \hspace{0.05cm}(X)} \ = \ $ { 7.39 3% } | ${\it \Gamma}_{{\hspace{-0.05cm} \rm L}, \hspace{0.05cm}(X)} \ = \ $ { 7.39 3% } | ||
| Line 46: | Line 46: | ||
{Berechnen Sie die differentielle Entropie der Laplaceverteilung für $\lambda = 1$. | {Berechnen Sie die differentielle Entropie der Laplaceverteilung für $\lambda = 1$. | ||
|type="{}"} | |type="{}"} | ||
| − | $h(Y) \ = \ $ { 2.443 3% } | + | $h(Y) \ = \ $ { 2.443 3% } $\ \rm bit$ |
| − | {Welche Kenngröße ${\it \Gamma}_{\hspace{-0.05cm} \rm L} $ ergibt sich für die Laplaceverteilung? | + | {Welche Kenngröße ${\it \Gamma}_{{\hspace{-0.05cm} \rm L}, \hspace{0.05cm}(Y)} $ ergibt sich für die Laplaceverteilung? |
|type="{}"} | |type="{}"} | ||
${\it \Gamma}_{{\hspace{-0.05cm} \rm L}, \hspace{0.05cm}(Y)} \ = \ $ { 14.78 3% } | ${\it \Gamma}_{{\hspace{-0.05cm} \rm L}, \hspace{0.05cm}(Y)} \ = \ $ { 14.78 3% } | ||
| Line 59: | Line 59: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' Obwohl in dieser Aufgabe das Ergebnis in „bit” angegeben werden soll, verwenden wir zur Herleitung den natürlichen Logarithmus. Dann gilt für die differentielle Entropie: | |
| − | $$h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp} | + | :$$h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp} |
\hspace{0.03cm}(\hspace{-0.03cm}f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm ln} \hspace{0.1cm} [f_X(x)] \hspace{0.1cm}{\rm d}x | \hspace{0.03cm}(\hspace{-0.03cm}f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm ln} \hspace{0.1cm} [f_X(x)] \hspace{0.1cm}{\rm d}x | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
Für die Exponentialverteilung sind die Integrationsgrenzen 0 und +∞ anzusetzen. In diesem Bereich wird die auf dem Angabenblatt angegebene WDF <i>f<sub>X</sub></i>(<i>x</i>) eingesetzt: | Für die Exponentialverteilung sind die Integrationsgrenzen 0 und +∞ anzusetzen. In diesem Bereich wird die auf dem Angabenblatt angegebene WDF <i>f<sub>X</sub></i>(<i>x</i>) eingesetzt: | ||
| − | $$h(X) | + | :$$h(X) =- \int_{0}^{\infty} \hspace{-0.15cm} |
\lambda \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x} | \lambda \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x} | ||
\hspace{0.05cm} \cdot \hspace{0.05cm} \left [ {\rm ln} \hspace{0.1cm} (\lambda) + | \hspace{0.05cm} \cdot \hspace{0.05cm} \left [ {\rm ln} \hspace{0.1cm} (\lambda) + | ||
| − | {\rm ln} \hspace{0.1cm} ({\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x})\right ]\hspace{0.1cm}{\rm d}x | + | {\rm ln} \hspace{0.1cm} ({\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x})\right ]\hspace{0.1cm}{\rm d}x |
| − | + | - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda) \cdot \int_{0}^{\infty} \hspace{-0.15cm} | |
\lambda \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x | \lambda \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x | ||
\hspace{0.1cm} + \hspace{0.1cm} \lambda \cdot \int_{0}^{\infty} \hspace{-0.15cm} | \hspace{0.1cm} + \hspace{0.1cm} \lambda \cdot \int_{0}^{\infty} \hspace{-0.15cm} | ||
| Line 74: | Line 74: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
Man erkennt: | Man erkennt: | ||
| − | + | * Der erste Integrand ist identisch mit der hier betrachteten WDF <i>f<sub>X</sub></i>(<i>x</i>). Das Integral über den gesamten Integrationsbereich ergibt somit 1. | |
| − | + | * Das zweite Integral entspricht genau der Definition des Mittelwertes <i>m</i><sub>1</sub> (Moment erster Ordnung). Für die Exponentialverteilung gilt <i>m</i><sub>1</sub> = 1/<i>λ</i>. Daraus folgt: | |
| − | $$h(X) = - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda) + 1 = | + | :$$h(X) = - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda) + 1 = |
- \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda) + \hspace{0.05cm} {\rm ln} \hspace{0.1cm} ({\rm e}) = {\rm ln} \hspace{0.1cm} ({\rm e}/\lambda) | - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda) + \hspace{0.05cm} {\rm ln} \hspace{0.1cm} ({\rm e}) = {\rm ln} \hspace{0.1cm} ({\rm e}/\lambda) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
Dieses Ergebnis ist mit der Zusatzeinheit „nat” zu versehen. Mit „log<sub>2</sub>” anstelle von „ln” erhält man die differentielle Entropie in „bit”: | Dieses Ergebnis ist mit der Zusatzeinheit „nat” zu versehen. Mit „log<sub>2</sub>” anstelle von „ln” erhält man die differentielle Entropie in „bit”: | ||
| − | $$h(X) = {\rm log}_2 \hspace{0.1cm} ({\rm e}/\lambda) | + | :$$h(X) = {\rm log}_2 \hspace{0.1cm} ({\rm e}/\lambda) |
\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda = 1{\rm :} | \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda = 1{\rm :} | ||
\hspace{0.3cm} h(X) = {\rm log}_2 \hspace{0.1cm} ({\rm e}) = \frac{{\rm ln} \hspace{0.1cm} ({\rm e})}{{\rm ln} \hspace{0.1cm} (2)} | \hspace{0.3cm} h(X) = {\rm log}_2 \hspace{0.1cm} ({\rm e}) = \frac{{\rm ln} \hspace{0.1cm} ({\rm e})}{{\rm ln} \hspace{0.1cm} (2)} | ||
\hspace{0.15cm}\underline{= 1.443\,{\rm bit}} | \hspace{0.15cm}\underline{= 1.443\,{\rm bit}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | ||
| − | $$h(X) = {\rm log}_2 \hspace{0.1cm} ({\rm e}/\lambda) = | + | '''(2)''' Unter Berücksichtigung der für die Exponentialverteilung gültigen Gleichung <i>σ</i><sup>2</sup> = 1/<i>λ</i><sup>2</sup> kann man das in der Teilaufgabe (1) gefundene Ergebnis wie folgt umformen: |
| − | + | : $$h(X) = {\rm log}_2 \hspace{0.1cm} ({\rm e}/\lambda) = | |
| + | {1}/{2}\cdot {\rm log}_2 \hspace{0.1cm} ({\rm e}^2/\lambda^2) | ||
= | = | ||
| − | + | {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ({\rm e}^2 \cdot \sigma^2) | |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
Ein Vergleich mit der geforderten Grundform 1/2 · log<sub>2</sub> (<i>Γ</i><sub>L</sub> · <i>σ</i><sup>2</sup>) führt zum Ergebnis: | Ein Vergleich mit der geforderten Grundform 1/2 · log<sub>2</sub> (<i>Γ</i><sub>L</sub> · <i>σ</i><sup>2</sup>) führt zum Ergebnis: | ||
| − | $${\it \Gamma}_{\rm L} = {\rm e}^2 \hspace{0.15cm}\underline{\approx 7.39} | + | $${\it \Gamma}_{{\hspace{-0.05cm} \rm L}, \hspace{0.05cm}(X)} = {\rm e}^2 \hspace{0.15cm}\underline{\approx 7.39} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | ||
| − | + | '''(3)''' Bei der Laplaceverteilung unterteilen wir den Integrationsbereich in zwei Teilbereiche: | |
| − | + | * <i>Y</i> negativ ⇒ Anteil <i>h</i><sub>neg</sub>(<i>Y</i>), | |
| + | * <i>Y</i> positiv ⇒ Anteil <i>h</i><sub>pos</sub>(<i>Y</i>). | ||
| + | |||
Die gesamte differentielle Entropie ergibt sich unter Berücksichtigung von <i>h</i><sub>neg</sub>(<i>Y</i>) = <i>h</i><sub>pos</sub>(<i>Y</i>) zu | Die gesamte differentielle Entropie ergibt sich unter Berücksichtigung von <i>h</i><sub>neg</sub>(<i>Y</i>) = <i>h</i><sub>pos</sub>(<i>Y</i>) zu | ||
| − | $$h(Y) = h_{\rm neg}(Y) + h_{\rm pos}(Y) = 2 \cdot h_{\rm pos}(Y) $$ | + | :$$h(Y) = h_{\rm neg}(Y) + h_{\rm pos}(Y) = 2 \cdot h_{\rm pos}(Y) $$ |
| − | $$\Rightarrow \hspace{0.3cm} h(Y) | + | :$$\Rightarrow \hspace{0.3cm} h(Y) = - 2 \cdot \int_{0}^{\infty} \hspace{-0.15cm} |
\lambda/2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}y} | \lambda/2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}y} | ||
\hspace{0.05cm} \cdot \hspace{0.05cm} \left [ {\rm ln} \hspace{0.1cm} (\lambda/2) + | \hspace{0.05cm} \cdot \hspace{0.05cm} \left [ {\rm ln} \hspace{0.1cm} (\lambda/2) + | ||
| − | {\rm ln} \hspace{0.1cm} ({\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}y})\right ]\hspace{0.1cm}{\rm d}y | + | {\rm ln} \hspace{0.1cm} ({\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}y})\right ]\hspace{0.1cm}{\rm d}y = - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda/2) \cdot \int_{0}^{\infty} \hspace{-0.15cm} |
| − | |||
\lambda \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}y}\hspace{0.1cm}{\rm d}y | \lambda \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}y}\hspace{0.1cm}{\rm d}y | ||
\hspace{0.1cm} + \hspace{0.1cm} \lambda \cdot \int_{0}^{\infty} \hspace{-0.15cm} | \hspace{0.1cm} + \hspace{0.1cm} \lambda \cdot \int_{0}^{\infty} \hspace{-0.15cm} | ||
| Line 111: | Line 113: | ||
Berücksichtigen wir wiederum, dass | Berücksichtigen wir wiederum, dass | ||
| − | + | * das erste Integral den Wert 1 ergibt (WDF–Fläche), und | |
| − | + | * das zweite Integral den Mittelwert <i>m</i><sub>1</sub> = 1/<i>λ</i> angibt, | |
| + | |||
so erhalten wir: | so erhalten wir: | ||
| Line 124: | Line 127: | ||
\hspace{0.15cm}\underline{= 2.443\,{\rm bit}} | \hspace{0.15cm}\underline{= 2.443\,{\rm bit}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | ||
| + | '''(4)''' Bei der Laplaceverteilung gilt der Zusammenhang <i>σ</i><sup>2</sup> = 2/<i>λ</i><sup>2</sup>. Damit erhält man: | ||
$$h(X) = {\rm log}_2 \hspace{0.1cm} (\frac{2{\rm e}}{\lambda}) = | $$h(X) = {\rm log}_2 \hspace{0.1cm} (\frac{2{\rm e}}{\lambda}) = | ||
| − | + | {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} (\frac{4{\rm e}^2}{\lambda^2}) | |
= | = | ||
| − | + | {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} (2 {\rm e}^2 \cdot \sigma^2) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\it \Gamma}_{{\hspace{-0.05cm} \rm L}, \hspace{0.05cm}(Y)} = 2 \cdot {\rm e}^2 \hspace{0.15cm}\underline{\approx 14.78} | |
| − | |||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Der <i>Γ</i><sub>L</sub>–Wert ist bei der Laplaceverteilung doppelt so groß wie bei der Exponentialverteilung. Damit ist offensichtlich, dass die Laplaceverteilung hinsichtlich der differentiellen Entropie <i>h</i>(<i>X</i>) deutlich besser ist als die Exponentialverteilung, wenn man von leistungsbegrenzten Signalen ausgeht. Unter der Nebenbedingung der Spitzenwertbegrenzung sind sowohl die Exponential– als auch die Laplaceverteilung völlig ungeeignet, ebenso wie die Gaußverteilung. Diese reichen alle bis ins Unendliche. | + | Der <i>Γ</i><sub>L</sub>–Wert ist bei der Laplaceverteilung doppelt so groß wie bei der Exponentialverteilung. |
| + | *Damit ist offensichtlich, dass die Laplaceverteilung hinsichtlich der differentiellen Entropie <i>h</i>(<i>X</i>) deutlich besser ist als die Exponentialverteilung, wenn man von leistungsbegrenzten Signalen ausgeht. | ||
| + | *Unter der Nebenbedingung der Spitzenwertbegrenzung sind sowohl die Exponential– als auch die Laplaceverteilung völlig ungeeignet, ebenso wie die Gaußverteilung. Diese reichen alle bis ins Unendliche. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 14:23, 9 June 2017
Wir betrachten hier die Wahrscheinlichkeitsdichtefunktionen (WDF) zweier wertkontinuierlicher Zufallsgrößen:
- Die Zufallsgröße $X$ ist exponentialverteilt (siehe obere Darstellung): Für $x<0$ ist $f_X(x) = 0$, und für positive $x$–Werte gilt:
- $$f_X(x) = \lambda \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.05cm}. $$
- Dagegen gilt für die laplaceverteilte Zufallsgröße $Y$ im gesamten Bereich$ - \infty < y < + \infty$ (untere Skizze):
- $$f_Y(y) = \lambda/2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}|y|}\hspace{0.05cm}.$$
Zu berechnen sind die differentiellen Entropien $h(X)$ und $h(Y)$ abhängig vom WDF–Parameter $\it \lambda$. Zum Beispiel gilt:
- $$h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}f_X)} \hspace{-0.55cm} f_X(x) \cdot {\rm log}_2 \hspace{0.1cm} [f_X(x)] \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$
Bei Verwendung von „log2” ist die Pseudo–Einheit „bit” anzufügen.
In den Teilaufgaben (2) und (4) ist die differentielle Entropie in folgender Form anzugeben: $$h(X) = {1}/{2} \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{{\hspace{-0.05cm} \rm L}, \hspace{0.05cm}(X)} \cdot \sigma^2) \hspace{0.5cm}{\rm bzw.} \hspace{0.5cm}h(Y) = {1}/{2} \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{{\hspace{-0.05cm} \rm L}, \hspace{0.05cm}(Y)} \cdot \sigma^2) \hspace{0.05cm}.$$ Zu ermitteln ist, durch welchen Faktor ${\it \Gamma}_{{\hspace{-0.05cm} \rm L}, \hspace{0.05cm}(X)}$ die Exponentialverteilung charakterisiert wird und welcher Faktor ${\it \Gamma}_{{\hspace{-0.05cm} \rm L}, \hspace{0.05cm}(Y)}$ sich für die Laplaceverteilung ergibt.
Hinweise:
- Die Aufgabe gehört zum Kapitel Differentielle Entropie.
- Nützliche Hinweise zur Lösung dieser Aufgabe finden Sie insbesondere auf der Seite Differentielle Entropie einiger leistungsbegrenzter Zufallsgrößen.
- Für die Varianz der exponentialverteiten Zufallsgröße $X$ gilt, wie in der Zusatzaufgabe 4.1Z hergeleitet: $\sigma^2 = 1/\lambda^2$.
- Die Varianz der laplaceverteiten Zufallsgröße $Y$ ist bei gleichem $\it \lambda$ doppelt so groß: $\sigma^2 = 2/\lambda^2$.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
- $$h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm ln} \hspace{0.1cm} [f_X(x)] \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$
Für die Exponentialverteilung sind die Integrationsgrenzen 0 und +∞ anzusetzen. In diesem Bereich wird die auf dem Angabenblatt angegebene WDF fX(x) eingesetzt:
- $$h(X) =- \int_{0}^{\infty} \hspace{-0.15cm} \lambda \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x} \hspace{0.05cm} \cdot \hspace{0.05cm} \left [ {\rm ln} \hspace{0.1cm} (\lambda) + {\rm ln} \hspace{0.1cm} ({\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x})\right ]\hspace{0.1cm}{\rm d}x - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda) \cdot \int_{0}^{\infty} \hspace{-0.15cm} \lambda \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x \hspace{0.1cm} + \hspace{0.1cm} \lambda \cdot \int_{0}^{\infty} \hspace{-0.15cm} \lambda \cdot x \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$
Man erkennt:
- Der erste Integrand ist identisch mit der hier betrachteten WDF fX(x). Das Integral über den gesamten Integrationsbereich ergibt somit 1.
- Das zweite Integral entspricht genau der Definition des Mittelwertes m1 (Moment erster Ordnung). Für die Exponentialverteilung gilt m1 = 1/λ. Daraus folgt:
- $$h(X) = - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda) + 1 = - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda) + \hspace{0.05cm} {\rm ln} \hspace{0.1cm} ({\rm e}) = {\rm ln} \hspace{0.1cm} ({\rm e}/\lambda) \hspace{0.05cm}.$$
Dieses Ergebnis ist mit der Zusatzeinheit „nat” zu versehen. Mit „log2” anstelle von „ln” erhält man die differentielle Entropie in „bit”:
- $$h(X) = {\rm log}_2 \hspace{0.1cm} ({\rm e}/\lambda) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda = 1{\rm :} \hspace{0.3cm} h(X) = {\rm log}_2 \hspace{0.1cm} ({\rm e}) = \frac{{\rm ln} \hspace{0.1cm} ({\rm e})}{{\rm ln} \hspace{0.1cm} (2)} \hspace{0.15cm}\underline{= 1.443\,{\rm bit}} \hspace{0.05cm}.$$
(2) Unter Berücksichtigung der für die Exponentialverteilung gültigen Gleichung σ2 = 1/λ2 kann man das in der Teilaufgabe (1) gefundene Ergebnis wie folgt umformen:
- $$h(X) = {\rm log}_2 \hspace{0.1cm} ({\rm e}/\lambda) = {1}/{2}\cdot {\rm log}_2 \hspace{0.1cm} ({\rm e}^2/\lambda^2) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ({\rm e}^2 \cdot \sigma^2) \hspace{0.05cm}.$$
Ein Vergleich mit der geforderten Grundform 1/2 · log2 (ΓL · σ2) führt zum Ergebnis: $${\it \Gamma}_{{\hspace{-0.05cm} \rm L}, \hspace{0.05cm}(X)} = {\rm e}^2 \hspace{0.15cm}\underline{\approx 7.39} \hspace{0.05cm}.$$
(3) Bei der Laplaceverteilung unterteilen wir den Integrationsbereich in zwei Teilbereiche:
- Y negativ ⇒ Anteil hneg(Y),
- Y positiv ⇒ Anteil hpos(Y).
Die gesamte differentielle Entropie ergibt sich unter Berücksichtigung von hneg(Y) = hpos(Y) zu
- $$h(Y) = h_{\rm neg}(Y) + h_{\rm pos}(Y) = 2 \cdot h_{\rm pos}(Y) $$
- $$\Rightarrow \hspace{0.3cm} h(Y) = - 2 \cdot \int_{0}^{\infty} \hspace{-0.15cm} \lambda/2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}y} \hspace{0.05cm} \cdot \hspace{0.05cm} \left [ {\rm ln} \hspace{0.1cm} (\lambda/2) + {\rm ln} \hspace{0.1cm} ({\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}y})\right ]\hspace{0.1cm}{\rm d}y = - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda/2) \cdot \int_{0}^{\infty} \hspace{-0.15cm} \lambda \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}y}\hspace{0.1cm}{\rm d}y \hspace{0.1cm} + \hspace{0.1cm} \lambda \cdot \int_{0}^{\infty} \hspace{-0.15cm} \lambda \cdot y \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}y}\hspace{0.1cm}{\rm d}y \hspace{0.05cm}.$$
Berücksichtigen wir wiederum, dass
- das erste Integral den Wert 1 ergibt (WDF–Fläche), und
- das zweite Integral den Mittelwert m1 = 1/λ angibt,
so erhalten wir:
$$h(Y) = - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda/2) + 1 =
- \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda/2) + \hspace{0.05cm} {\rm ln} \hspace{0.1cm} ({\rm e}) = {\rm ln} \hspace{0.1cm} (2{\rm e}/\lambda)
\hspace{0.05cm}.$$
Da das Ergebnis in „bit” gefordert ist, muss noch „ln” durch „log2” ersetzt werden:
$$h(Y) = {\rm log}_2 \hspace{0.1cm} (2{\rm e}/\lambda)
\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda = 1{\rm :}
\hspace{0.3cm} h(Y) = {\rm log}_2 \hspace{0.1cm} (2{\rm e})
\hspace{0.15cm}\underline{= 2.443\,{\rm bit}}
\hspace{0.05cm}.$$
(4) Bei der Laplaceverteilung gilt der Zusammenhang σ2 = 2/λ2. Damit erhält man: $$h(X) = {\rm log}_2 \hspace{0.1cm} (\frac{2{\rm e}}{\lambda}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} (\frac{4{\rm e}^2}{\lambda^2}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} (2 {\rm e}^2 \cdot \sigma^2) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\it \Gamma}_{{\hspace{-0.05cm} \rm L}, \hspace{0.05cm}(Y)} = 2 \cdot {\rm e}^2 \hspace{0.15cm}\underline{\approx 14.78} \hspace{0.05cm}.$$ Der ΓL–Wert ist bei der Laplaceverteilung doppelt so groß wie bei der Exponentialverteilung.
- Damit ist offensichtlich, dass die Laplaceverteilung hinsichtlich der differentiellen Entropie h(X) deutlich besser ist als die Exponentialverteilung, wenn man von leistungsbegrenzten Signalen ausgeht.
- Unter der Nebenbedingung der Spitzenwertbegrenzung sind sowohl die Exponential– als auch die Laplaceverteilung völlig ungeeignet, ebenso wie die Gaußverteilung. Diese reichen alle bis ins Unendliche.