Difference between revisions of "Aufgaben:Exercise 4.Ten: QPSK Channel Capacity"
| Line 21: | Line 21: | ||
sollen in der Teilaufgabe (3) in Bezug gesetzt werden zu zwei Shannon–Grenzkurven, die jeweils für eine Gaußsche Eingangsverteilung gültig sind: | sollen in der Teilaufgabe (3) in Bezug gesetzt werden zu zwei Shannon–Grenzkurven, die jeweils für eine Gaußsche Eingangsverteilung gültig sind: | ||
| − | :$$C_1( E_{\rm B}/{N_0}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2\ | + | :$$C_1( E_{\rm B}/{N_0}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2\cdot R \cdot E_{\rm B}}{N_0}) ,$$ |
| − | :$$C_2( E_{\rm B}/{N_0}) = {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { R\ | + | :$$C_2( E_{\rm B}/{N_0}) = {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { R \cdot E_{\rm B}}{N_0}) .$$ |
Die beiden Kurven geben gleichzeitig die maximale Coderate <i>R</i> an, mit der durch lange Kanalcodes eine fehlerfreie Übertragung entsprechend dem [[Informationstheorie/Anwendung_auf_die_Digitalsignalübertragung#Definition_und_Bedeutung_der_Kanalkapazit.C3.A4t|Kanalcodierungstheorem]] möglich ist. Natürlich gelten für <i>C</i><sub>1</sub>(<i>E</i><sub>B</sub>/<i>N</i><sub>0</sub>) bzw. <i>C</i><sub>2</sub>(<i>E</i><sub>B</sub>/<i>N</i><sub>0</sub>) unterschiedliche Randbedingungen. Welche, sollen Sie herausfinden. | Die beiden Kurven geben gleichzeitig die maximale Coderate <i>R</i> an, mit der durch lange Kanalcodes eine fehlerfreie Übertragung entsprechend dem [[Informationstheorie/Anwendung_auf_die_Digitalsignalübertragung#Definition_und_Bedeutung_der_Kanalkapazit.C3.A4t|Kanalcodierungstheorem]] möglich ist. Natürlich gelten für <i>C</i><sub>1</sub>(<i>E</i><sub>B</sub>/<i>N</i><sub>0</sub>) bzw. <i>C</i><sub>2</sub>(<i>E</i><sub>B</sub>/<i>N</i><sub>0</sub>) unterschiedliche Randbedingungen. Welche, sollen Sie herausfinden. | ||
| Line 34: | Line 34: | ||
*Die Aufgabe gehört zum Kapitel [[Informationstheorie/AWGN–Kanalkapazität_bei_wertkontinuierlichem_Eingang|AWGN–Kanalkapazität bei wertkontinuierlichem Eingang]]. | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/AWGN–Kanalkapazität_bei_wertkontinuierlichem_Eingang|AWGN–Kanalkapazität bei wertkontinuierlichem Eingang]]. | ||
*Bezug genommen wird insbesondere auf die Seite [[Informationstheorie/AWGN–Kanalkapazität_bei_wertdiskretem_Eingang#Maximale_Coderate_f.C3.BCr_QAM.E2.80.93Strukturen|Maximale Coderate für QAM-Strukturen]]. | *Bezug genommen wird insbesondere auf die Seite [[Informationstheorie/AWGN–Kanalkapazität_bei_wertdiskretem_Eingang#Maximale_Coderate_f.C3.BCr_QAM.E2.80.93Strukturen|Maximale Coderate für QAM-Strukturen]]. | ||
| − | |||
| Line 72: | Line 71: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | [[File:P_ID2958__Inf_A_4_10a.png|right|]] | + | [[File:P_ID2958__Inf_A_4_10a.png|right|frame|QPSK– und 4–QAM–Signalraumkonstellation]] |
'''(1)''' Die Grafik zeigt die Signalraumkonstellationen für | '''(1)''' Die Grafik zeigt die Signalraumkonstellationen für | ||
| − | + | * <i>Quaternary Phase Shift Keying</i> (QPSK), und | |
| − | + | * vierstufige Quadraturamplitudenmodulation (4–QAM). | |
| − | |||
| − | + | Letztere wird auch als [[Informationstheorie/Anwendung_auf_die_Digitalsignalübertragung#Definition_und_Bedeutung_der_Kanalkapazit.C3.A4t|π/4–QPSK]] bezeichnet. Beide sind aus informationstheoretischer Sicht identisch ⇒ <u>Antwort NEIN</u>. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''(2)''' Richtig ist der <u>Lösungsvorschlag 1</u>: | |
| − | + | *Die 4–QAM kann man als zwei BPSK–Konstellationen in orthogonalen Ebenen betrachten, wobei die Energie pro Informationsbit (<i>E</i><sub>B</sub>) in beiden Fällen gleich ist. | |
| − | : | + | *Da entsprechend der Teilaufgabe (1) die 4–QAM mit der QSPK identisch ist, gilt tatsächlich: |
| + | :$$C_{\rm QPSK}( E_{\rm B}/{N_0}) = 2 \cdot C_{\rm BPSK}( E_{\rm B}/{N_0}).$$ | ||
| − | Richtig sind also die <u>Lösungsvorschläge 1, 2 und 4</u>. | + | '''(3)''' In der unteren Grafik sind die beiden angegebenen Shannon–Grenzkurven zusammen mit <i>C</i><sub>BPSK</sub>(<i>E</i><sub>B</sub>/<i>N</i><sub>0</sub>) und <i>C</i><sub>QPSK</sub>(<i>E</i><sub>B</sub>/<i>N</i><sub>0</sub>) skizziert: |
| + | [[File:P_ID2959__Inf_A_4_1c.png|right|frame|Vier Kapazitätskurven mit unterschiedlichen Aussagen]] | ||
| + | :$$C_1( E_{\rm B}/{N_0}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2 \cdot R \cdot E_{\rm B}}{N_0}) ,$$ | ||
| + | :$$C_2( E_{\rm B}/{N_0}) = {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { R \cdot E_{\rm B}}{N_0}) .$$ | ||
| + | Man erkennt aus dieser Skizze: | ||
| + | *Die grün–gestrichelte Kurve <i>C</i><sub>1</sub>(<i>E</i><sub>B</sub>/<i>N</i><sub>0</sub>) gilt für den AWGN–Kanal mit gaußverteiltem Eingang. Für die Coderate <i>R</i> =1 sind nach dieser Kurve 10 · lg(<i>E</i><sub>B</sub>/<i>N</i><sub>0</sub>) = 1.76 dB erforderlich. Für <i>R</i> = 2 benötigt man dagegen 10 · lg(<i>E</i><sub>B</sub>/<i>N</i><sub>0</sub>) = 5.74 dB. | ||
| + | *Die blau–gestrichelte Kurve <i>C</i><sub>2</sub>(<i>E</i><sub>B</sub>/<i>N</i><sub>0</sub>) gibt die Shannon–Grenze für <i>K</i> = 2 parallele Gaußkanäle an. Hier benötigt man 10 · lg(<i>E</i><sub>B</sub>/<i>N</i><sub>0</sub>) = 0 dB für <i>R</i> = 1 bzw. 10 · lg(<i>E</i><sub>B</sub>/<i>N</i><sub>0</sub>) = 1.76 dB für <i>R</i> = 2. | ||
| + | * Die eindimensionale BPSK liegt im gesamten Bereich unterhalb von <i>C</i><sub>1</sub> und damit natürlich auch unterhalb von <i>C</i><sub>2</sub> > <i>C</i><sub>1</sub>. | ||
| + | * Die zweidimensionale QPSK liegt erwartungsgemäß unter der für sie relevanten Grenzkurve <i>C</i><sub>2</sub>. Sie liegt aber im unteren Bereich (bis nahezu 6 dB) oberhalb von <i>C</i><sub>1</sub>. | ||
| + | |||
| + | ⇒ Richtig sind also die <u>Lösungsvorschläge 1, 2 und 4</u>. | ||
'''(4)''' Die <i>C</i><sub>QPSK</sub>(<i>E</i><sub>S</sub>/<i>N</i><sub>0</sub>)–Kurve kann ebenfalls aus <i>C</i><sub>BPSK</sub>(<i>E</i><sub>S</sub>/<i>N</i><sub>0</sub>) konstruiert werden und zwar | '''(4)''' Die <i>C</i><sub>QPSK</sub>(<i>E</i><sub>S</sub>/<i>N</i><sub>0</sub>)–Kurve kann ebenfalls aus <i>C</i><sub>BPSK</sub>(<i>E</i><sub>S</sub>/<i>N</i><sub>0</sub>) konstruiert werden und zwar | ||
| − | + | * zum einen durch Verdopplung: | |
| − | $$C_{\rm BPSK}(10 \cdot {\rm lg} \hspace{0.1cm}E_{\rm S}/{N_0}) | + | :$$C_{\rm BPSK}(10 \cdot {\rm lg} \hspace{0.1cm}E_{\rm S}/{N_0}) |
| − | \hspace{0. | + | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} |
2 \cdot C_{\rm BPSK}(10 \cdot {\rm lg} \hspace{0.1cm}E_{\rm S}/{N_0}) ,$$ | 2 \cdot C_{\rm BPSK}(10 \cdot {\rm lg} \hspace{0.1cm}E_{\rm S}/{N_0}) ,$$ | ||
| − | + | * sowie durch eine Verschiebung um 3 dB nach rechts: | |
| − | $$C_{\rm QPSK}(10 \cdot {\rm lg} \hspace{0.1cm}E_{\rm S}/{N_0}) | + | :$$C_{\rm QPSK}(10 \cdot {\rm lg} \hspace{0.1cm}E_{\rm S}/{N_0}) |
= | = | ||
2 \cdot C_{\rm BPSK}(10 \cdot {\rm lg} \hspace{0.1cm}E_{\rm S}/{N_0} - 3\,{\rm dB}) .$$ | 2 \cdot C_{\rm BPSK}(10 \cdot {\rm lg} \hspace{0.1cm}E_{\rm S}/{N_0} - 3\,{\rm dB}) .$$ | ||
Revision as of 16:21, 14 June 2017
Gegeben sind die AWGN–Kanalkapazitätsgrenzkurven für die beiden Modulationsverfahren
- Binary Phase Shift Keying (BPSK),
- Quaternary Phase Shift Keying (4–PSK oder auch QPSK).
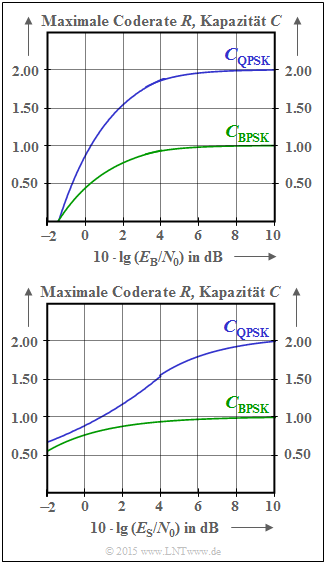
Die Kanalkapazitäten CBPSK und CQPSK geben gleichzeitig die maximale Coderate R an, mit der bei BPSK (bzw. QPSK) mit geeigneter Kanalcodierung die Bitfehlerwahrscheinlichkeit „pB ≡ 0” asymptotisch erreichbar ist.
Das obere Diagramm zeigt die Abhängigkeit von der Kenngröße 10 · lg (EB/N0) in dB, wobei EB die „Energie pro Informationsbit” angibt:
- Für große EB/N0–Werte liefert die BPSK–Kurve die maximale Coderate R ≈ 1. *Aus der QPSK–Kurve kann dagegen R ≈ 2 abgelesen werden
Die Kapazitätskurven für digitalen Eingang (jeweils mit der Einheit „bit/Symbol”),
- grüne Kurve CBPSK(EB/N0) und
- blaue Kurve CQPSK(EB/N0)
sollen in der Teilaufgabe (3) in Bezug gesetzt werden zu zwei Shannon–Grenzkurven, die jeweils für eine Gaußsche Eingangsverteilung gültig sind:
- $$C_1( E_{\rm B}/{N_0}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2\cdot R \cdot E_{\rm B}}{N_0}) ,$$
- $$C_2( E_{\rm B}/{N_0}) = {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { R \cdot E_{\rm B}}{N_0}) .$$
Die beiden Kurven geben gleichzeitig die maximale Coderate R an, mit der durch lange Kanalcodes eine fehlerfreie Übertragung entsprechend dem Kanalcodierungstheorem möglich ist. Natürlich gelten für C1(EB/N0) bzw. C2(EB/N0) unterschiedliche Randbedingungen. Welche, sollen Sie herausfinden.
Die Abszisse im unteren Diagramm ist dagegen 10 · lg (ES/N0) mit der „Energie pro Symbol” (ES). Zu erkennen ist, dass die beiden Endwerte gegenüber der oberen Darstellung nicht verändert werden:
- $$C_{\rm BPSK}( E_{\rm S}/{N_0} \to \infty) = C_{\rm BPSK}( E_{\rm B}/{N_0} \to \infty) = 1 \ \rm bit/Symbol,$$
- $$C_{\rm QPSK}( E_{\rm S}/{N_0} \to \infty) = C_{\rm QPSK}( E_{\rm B}/{N_0} \to \infty) = 2 \ \rm bit/Symbol.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel AWGN–Kanalkapazität bei wertkontinuierlichem Eingang.
- Bezug genommen wird insbesondere auf die Seite Maximale Coderate für QAM-Strukturen.
Fragebogen
Musterlösung
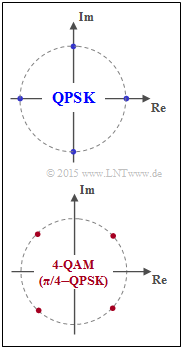
(1) Die Grafik zeigt die Signalraumkonstellationen für
- Quaternary Phase Shift Keying (QPSK), und
- vierstufige Quadraturamplitudenmodulation (4–QAM).
Letztere wird auch als π/4–QPSK bezeichnet. Beide sind aus informationstheoretischer Sicht identisch ⇒ Antwort NEIN.
(2) Richtig ist der Lösungsvorschlag 1:
- Die 4–QAM kann man als zwei BPSK–Konstellationen in orthogonalen Ebenen betrachten, wobei die Energie pro Informationsbit (EB) in beiden Fällen gleich ist.
- Da entsprechend der Teilaufgabe (1) die 4–QAM mit der QSPK identisch ist, gilt tatsächlich:
- $$C_{\rm QPSK}( E_{\rm B}/{N_0}) = 2 \cdot C_{\rm BPSK}( E_{\rm B}/{N_0}).$$
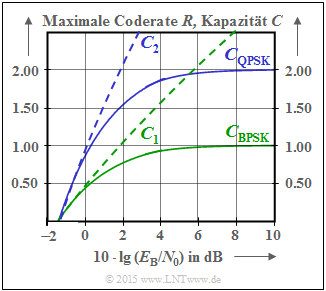
(3) In der unteren Grafik sind die beiden angegebenen Shannon–Grenzkurven zusammen mit CBPSK(EB/N0) und CQPSK(EB/N0) skizziert:
- $$C_1( E_{\rm B}/{N_0}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2 \cdot R \cdot E_{\rm B}}{N_0}) ,$$
- $$C_2( E_{\rm B}/{N_0}) = {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { R \cdot E_{\rm B}}{N_0}) .$$
Man erkennt aus dieser Skizze:
- Die grün–gestrichelte Kurve C1(EB/N0) gilt für den AWGN–Kanal mit gaußverteiltem Eingang. Für die Coderate R =1 sind nach dieser Kurve 10 · lg(EB/N0) = 1.76 dB erforderlich. Für R = 2 benötigt man dagegen 10 · lg(EB/N0) = 5.74 dB.
- Die blau–gestrichelte Kurve C2(EB/N0) gibt die Shannon–Grenze für K = 2 parallele Gaußkanäle an. Hier benötigt man 10 · lg(EB/N0) = 0 dB für R = 1 bzw. 10 · lg(EB/N0) = 1.76 dB für R = 2.
- Die eindimensionale BPSK liegt im gesamten Bereich unterhalb von C1 und damit natürlich auch unterhalb von C2 > C1.
- Die zweidimensionale QPSK liegt erwartungsgemäß unter der für sie relevanten Grenzkurve C2. Sie liegt aber im unteren Bereich (bis nahezu 6 dB) oberhalb von C1.
⇒ Richtig sind also die Lösungsvorschläge 1, 2 und 4.
(4) Die CQPSK(ES/N0)–Kurve kann ebenfalls aus CBPSK(ES/N0) konstruiert werden und zwar
- zum einen durch Verdopplung:
- $$C_{\rm BPSK}(10 \cdot {\rm lg} \hspace{0.1cm}E_{\rm S}/{N_0}) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 2 \cdot C_{\rm BPSK}(10 \cdot {\rm lg} \hspace{0.1cm}E_{\rm S}/{N_0}) ,$$
- sowie durch eine Verschiebung um 3 dB nach rechts:
- $$C_{\rm QPSK}(10 \cdot {\rm lg} \hspace{0.1cm}E_{\rm S}/{N_0}) = 2 \cdot C_{\rm BPSK}(10 \cdot {\rm lg} \hspace{0.1cm}E_{\rm S}/{N_0} - 3\,{\rm dB}) .$$
Richtig sind die beiden ersten Lösungsvorschläge, wobei der zweite Vorschlag berücksichtigt, dass bei QPSK die Energie in einer Dimension nur ES/2 beträgt.