Aufgaben:Exercise 2.11: Envelope Demodulation of an SSB Signal

• Return to book

Hüllkurve bei Einseitenband–Modulation

Wir betrachten die Übertragung des Cosinussignals

$$ q(t) = A_{\rm N} \cdot \cos(\omega_{\rm N} \cdot t)$$

gemäß dem Modulationsverfahren „OSB–AM mit Träger”. Beim Empfänger wird das hochfrequente Signal mittels eines Hüllkurvendemodulators in den NF-Bereich zurückgesetzt

Der Kanal wird als ideal vorausgesetzt, so dass das Empfangssignal $r(t)$ identisch mit dem Sendesignal $s(t)$ ist. Mit dem Seitenband–zu–Träger–Verhältnis

$$ \mu = \frac{A_{\rm N}}{2 \cdot A_{\rm T}}$$

kann für das äquivalente Tiefpass–Signal auch geschrieben werden:

$$r_{\rm TP}(t) = A_{\rm T} \cdot \left( 1 + \mu \cdot {\rm e}^{{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\omega_{\rm N}\cdot \hspace{0.03cm}\hspace{0.03cm}t} \right) \hspace{0.05cm}$$

Die Hüllkurve – also der Betrag dieses komplexen Signals – kann durch geometrische Überlegungen ermittelt werden. Man erhält abhängig vom Parameter $μ$:

$$a(t ) = A_{\rm T} \cdot \sqrt{1+ \mu^2 + 2 \mu \cdot \cos(\omega_{\rm N} \cdot t)}\hspace{0.05cm}.$$

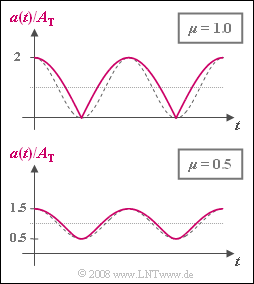
In der Grafik ist die zeitabhängige Hüllkurve a(t) für $μ = 1$ und $μ = 0.5$ dargestellt. Als gestrichelte Vergleichskurven sind jeweils die in der Amplitude angepassten Cosinusschwingungen eingezeichnet, die für eine verzerrungsfreie Demodulation Voraussetzung wären.

Das periodische Signal $a(t)$ kann durch eine Fourierreihe angenähert werden:

$$a(t ) = A_{\rm 0} + A_{\rm 1} \cdot \cos(\omega_{\rm N} \cdot t) + A_{\rm 2} \cdot \cos(2\omega_{\rm N} \cdot t)+ A_{\rm 3} \cdot \cos(3\omega_{\rm N} \cdot t)\hspace{0.05cm}+\text{...}$$

Die Fourierkoeffizienten wurden mit Hilfe eines Simulationsprogrammes ermittelt. Für $μ = 1$ ergaben sich folgende Werte:

$$A_{\rm 0} = 1.273\,{\rm V},\hspace{0.3cm} A_{\rm 1} = 0.849\,{\rm V},\hspace{0.3cm}A_{\rm 2} = -0.170\,{\rm V},\hspace{0.3cm} A_{\rm 3} = 0.073\,{\rm V},\hspace{0.3cm}A_{\rm 4} = 0.040\,{\rm V} \hspace{0.05cm}.$$

Entsprechend ergab die Simulation mit $μ = 0.5$:

$$A_{\rm 0} = 1.064\,{\rm V},\hspace{0.3cm} A_{\rm 1} = 0.484\,{\rm V},\hspace{0.3cm}A_{\rm 2} = 0.058\,{\rm V} \hspace{0.05cm}.$$

Die hier nicht angegebenen Werte können bei der Klirrfaktorberechnung vernachlässigt werden. Das Sinkensignal $v(t)$ ergibt sich aus $a(t)$ wie folgt:

$$v(t) = 2 \cdot [a(t ) - A_{\rm 0}] \hspace{0.05cm}.$$

Der Faktor $2$ korrigiert dabei die Amplitudenminderung durch die ESB–AM, während die Subtraktion des Gleichsignalkoeffizienten $A_0$ den Einfluss des Hochpasses innerhalb des Hüllkurvendemodulators berücksichtigt.

Für die Teilaufgaben (1) bis (3) wird $A_{\rm N} = 2 \ \rm V$, $A_{\rm T} = 1 \ \rm V$ und somit $μ = 1$ vorausgesetzt, während ab Frage (4) für den Parameter $μ = 0.5$   ⇒   $A_{\rm N} = A_{\rm T} = 1 \ \rm V$ gelten soll.

Hinweise:

• Die Aufgabe gehört zum Kapitel Einseitenbandmodulation.
• Bezug genommen wird insbesondere auf die Seite Seitenband-zu-Träger-Verhältnis.
• Vergleichen Sie Ihre Ergebnisse auch mit der Faustformel, die besagt, dass bei der Hüllkurvendemodulation eines ESB–AM–Signals mit dem Seitenband–zu–Träger–Verhältnis $μ$ der Klirrfaktor $K ≈ μ/4$ beträgt.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1 Geben Sie den Maximalwert und den Minimalwert des Sinkensignals $v(t)$ für $μ = 1$ an.

$v_{\rm max} \ = \ $ $\ \rm V$

$v_{\rm min} \ = \ $ $\ \rm V$

2 Berechnen Sie den Klirrfaktor für $μ = 1$.

$K \ = \ $ $\ \text{%}$

3 Woran erkennt man die nichtlinearen Verzerrungen im vorliegenden Signal $v(t)$?

	Die untere Cosinushalbwelle ist spitzförmiger als die obere.
	Der Gleichsignalanteil ${\rm Ε}[v(t)] = 0$.

4 Geben Sie den Maximalwert und den Minimalwert des Sinkensignals $v(t)$ für $μ = 0.5$ an.

$v_{\rm max} \ = \ $ $\ \rm V$

$v_{\rm min} \ = \ $ $\ \rm V$

5 Berechnen Sie den Klirrfaktor für $μ = 0.5$.

$K \ = \ $ $\ \text{%}$

6 Geben Sie eine obere Schranke $K_{\rm max}$ für den Klirrfaktor bei ZSB–AM mit $m = 0.5$ und Hüllkurvendemodulation an, wenn ein Seitenband durch den Kanal gedämpft wird.

$K_{\rm max} \ = \ $ $\ \text{%}$

Musterlösung

Solution

1.Der Maximalwert $a_{max} = 2 V$ und der Minimalwert $a_{min} = 0$ können aus der Grafik abgelesen oder über die angegebene Gleichung berechnet werden: $$ a_{\rm max} = A_{\rm T} \cdot \sqrt{1+ \mu^2 + 2 \mu}= A_{\rm T} \cdot (1+ \mu) = 2\,{\rm V} \hspace{0.05cm},$$ $$a_{\rm min} = A_{\rm T} \cdot \sqrt{1+ \mu^2 - 2 \mu}= A_{\rm T} \cdot (1- \mu) = 0 \hspace{0.05cm}.$$ Für die Extremwerte des Sinkensignals folgt daraus: $$ v_{\rm max} = 2 \cdot [a_{\rm max} - A_{\rm 0}] = 2 \cdot [2\,{\rm V} - 1.273\,{\rm V}] \hspace{0.15cm}\underline {=1.454\,{\rm V}}\hspace{0.05cm},$$ $$ v_{\rm min} = -2 \cdot A_{\rm 0} \hspace{0.15cm}\underline {= -2.546\,{\rm V}}\hspace{0.05cm}.$$

2. Unter Vernachlässigung der Fourierkoeffizienten $A_5$, $A_6$, usw. erhält man: $$K = \frac{\sqrt{A_2^2 + A_3^2+ A_4^2 }}{A_1}= \frac{\sqrt{0.170^2 + 0.073^2 + 0.040^2 }{\,\rm V}}{0.849\,{\rm V}}\hspace{0.15cm}\underline { \approx 22.3 \%}.$$ Die Näherung $K ≈ μ/4$ liefert hier den Wert $25%$.

3. Nur der erste Lösungsvorschlag ist richtig. Aufgrund des Hochpasses innerhalb des HKD wäre der Gleichsignalanteil auch dann 0, wenn keine Verzerrungen vorlägen.

4. Analog zur Teilaufgabe a) gilt hier: $$v_{\rm max} = 2 \cdot [a_{\rm max} - A_{\rm 0}] = 2 \cdot [1.5\,{\rm V} - 1.064\,{\rm V}] \hspace{0.15cm}\underline {= 0.872\,{\rm V}}\hspace{0.05cm},$$ $$ v_{\rm min} = -2 \cdot A_{\rm 0} \hspace{0.15cm}\underline {= -2.128\,{\rm V}}\hspace{0.05cm}.$$ 5. Bei kleinerem Seitenband–zu–Träger–Verhältnis ergibt sich auch ein kleinerer Klirrfaktor: $$K = \frac{0.058{\,\rm V}}{0.484\,{\rm V}}\hspace{0.15cm}\underline { \approx 12 \%}.$$ Die Näherung $K ≈ μ/4$ ergibt hier $12.5%$. Daraus kann geschlossen werden, dass die angegebene Faustformel bei kleinerem $μ$ genauer ist.

6.Der Klirrfaktor ist dann am größten, wenn eines der Seitenbänder völlig abgeschnitten wird. Da aber der Hüllkurvendemodulator keinerlei Kenntnis davon hat, ob eine ESB–AM oder eine durch $H_K(f)$ beeinträchtigte ZSB–AM vorliegt, gibt $K_{max} ≈ μ/4$ gleichzeitig eine obere Schranke für die ZSB–AM an.

Ein Vergleich der Parameter $m = A_N/A_T$ und $μ = A_N/(2A_T)$ führt zum Ergebnis: $$K_{\rm max} = \frac{\mu}{4} = \frac{m}{8} \hspace{0.15cm}\underline {=6.25 \%}.$$