Difference between revisions of "Aufgaben:Exercise 2.13: Quadrature Amplitude Modulation"
m (Guenter verschob die Seite 2.12 Quadratur-Amplitudenmodulation nach 2.13 Quadratur-Amplitudenmodulation (QAM)) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
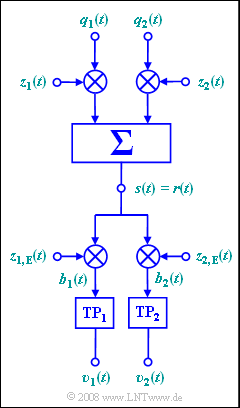
| − | [[File:P_ID1055__Mod_A_2_11.png|right|]] | + | [[File:P_ID1055__Mod_A_2_11.png|right|frame|Betrachtetes Modell der Quadratur–Amplitudenmodulation]] |
| − | Die durch die Grafik erklärte Quadratur–Amplitudenmodulation erlaubt unter gewissen Randbedingungen, die in dieser Aufgabe | + | Die durch die Grafik erklärte ''Quadratur–Amplitudenmodulation'' (QAM) erlaubt unter gewissen Randbedingungen, die in dieser Aufgabe herausgefunden werden sollen, die gleichzeitige Übertragung von zwei Quellensignalen $q_1(t)$ und $q_2(t)$ über den gleichen Kanal. In dieser Aufgabe gelte mit $A_1 = A_2 = 2\ \rm V$: |
| − | $$q_1(t) = A_1 \cdot \cos(2 \pi \cdot f_{\rm 1} \cdot t),$$ | + | :$$q_1(t) = A_1 \cdot \cos(2 \pi \cdot f_{\rm 1} \cdot t),$$ |
| − | $$q_2(t) = A_2 \cdot \sin(2 \pi \cdot f_{\rm 2} \cdot t)\hspace{0.05cm}.$$ | + | :$$q_2(t) = A_2 \cdot \sin(2 \pi \cdot f_{\rm 2} \cdot t)\hspace{0.05cm}.$$ |
| − | Die vier in der Grafik eingezeichneten Trägersignale lauten mit $ | + | Die vier in der Grafik eingezeichneten Trägersignale lauten mit $ω_{\rm T} = 2π · 25\ \rm kHz$: |
| − | $$z_1(t) = \cos(\omega_{\rm T} \cdot t),$$ | + | :$$z_1(t) = \cos(\omega_{\rm T} \cdot t),$$ |
| − | $$ z_2(t) = \sin(\omega_{\rm T} \cdot t),$$ | + | :$$ z_2(t) = \sin(\omega_{\rm T} \cdot t),$$ |
| − | $$ z_{1,{\rm E}}(t) = 2 \cdot \cos(\omega_{\rm T} \cdot t + \Delta \phi_{\rm T}),$$ | + | :$$ z_{1,{\rm E}}(t) = 2 \cdot \cos(\omega_{\rm T} \cdot t + \Delta \phi_{\rm T}),$$ |
| − | $$ z_{2,{\rm E}}(t) = 2 \cdot \sin(\omega_{\rm T} \cdot t + \Delta \phi_{\rm T})\hspace{0.05cm}.$$ | + | :$$ z_{2,{\rm E}}(t) = 2 \cdot \sin(\omega_{\rm T} \cdot t + \Delta \phi_{\rm T})\hspace{0.05cm}.$$ |
| − | Die beiden Tiefpässe mit den Eingangssignalen $b_1(t)$ und $b_2(t)$ entfernen jeweils alle Frequenzanteile $|f| > | + | Die beiden Tiefpässe mit den Eingangssignalen $b_1(t)$ und $b_2(t)$ entfernen jeweils alle Frequenzanteile $|f| > f_{\rm T}$. |
| − | '' | + | ''Hinweise:'' |
| − | + | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Weitere_AM–Varianten|WeitereAM–Variantenn]]. | |
| − | Gegeben sind folgende trigonometrischen Umformungen: | + | *Bezug genommen wird insbesondere auf die Seite [[Modulationsverfahren/Weitere_AM–Varianten#Quadratur.E2.80.93Amplitudenmodulation_.28QAM.29|Quadratur-Amplitudenmodulation (QAM)]]. |
| − | $$\cos(\alpha) \cdot \cos(\beta) = | + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. |
| − | $$ \sin(\alpha) \cdot \sin(\beta) = | + | *Anzumerken ist, dass hier die Trägersignale $z_2(t)$ und $z_{2,{\rm E}}(t)$ mit positivem Vorzeichen angesetzt wurden. Oft – so auch im Theorieteil – werden diese Trägersignale als „Minus–Sinus” angegeben. |
| − | $$\sin(\alpha) \cdot \cos(\beta) = | + | *Gegeben sind folgende trigonometrischen Umformungen: |
| + | :$$ \cos(\alpha) \cdot \cos(\beta) = 1/2 \cdot \left[ \cos(\alpha - \beta)+ \cos(\alpha + \beta) \right],$$ | ||
| + | :$$ \sin(\alpha) \cdot \sin(\beta) = 1/2 \cdot \left[ \cos(\alpha - \beta)- \cos(\alpha + \beta) \right],$$ | ||
| + | :$$ \sin(\alpha) \cdot \cos(\beta) = 1/2 \cdot \left[ \sin(\alpha - \beta)+ \sin(\alpha + \beta) \right] \hspace{0.05cm}.$$ | ||
===Fragebogen=== | ===Fragebogen=== | ||
Revision as of 11:30, 4 July 2017
Die durch die Grafik erklärte Quadratur–Amplitudenmodulation (QAM) erlaubt unter gewissen Randbedingungen, die in dieser Aufgabe herausgefunden werden sollen, die gleichzeitige Übertragung von zwei Quellensignalen $q_1(t)$ und $q_2(t)$ über den gleichen Kanal. In dieser Aufgabe gelte mit $A_1 = A_2 = 2\ \rm V$:
- $$q_1(t) = A_1 \cdot \cos(2 \pi \cdot f_{\rm 1} \cdot t),$$
- $$q_2(t) = A_2 \cdot \sin(2 \pi \cdot f_{\rm 2} \cdot t)\hspace{0.05cm}.$$
Die vier in der Grafik eingezeichneten Trägersignale lauten mit $ω_{\rm T} = 2π · 25\ \rm kHz$:
- $$z_1(t) = \cos(\omega_{\rm T} \cdot t),$$
- $$ z_2(t) = \sin(\omega_{\rm T} \cdot t),$$
- $$ z_{1,{\rm E}}(t) = 2 \cdot \cos(\omega_{\rm T} \cdot t + \Delta \phi_{\rm T}),$$
- $$ z_{2,{\rm E}}(t) = 2 \cdot \sin(\omega_{\rm T} \cdot t + \Delta \phi_{\rm T})\hspace{0.05cm}.$$
Die beiden Tiefpässe mit den Eingangssignalen $b_1(t)$ und $b_2(t)$ entfernen jeweils alle Frequenzanteile $|f| > f_{\rm T}$.
Hinweise:
- Die Aufgabe gehört zum Kapitel WeitereAM–Variantenn.
- Bezug genommen wird insbesondere auf die Seite Quadratur-Amplitudenmodulation (QAM).
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Anzumerken ist, dass hier die Trägersignale $z_2(t)$ und $z_{2,{\rm E}}(t)$ mit positivem Vorzeichen angesetzt wurden. Oft – so auch im Theorieteil – werden diese Trägersignale als „Minus–Sinus” angegeben.
- Gegeben sind folgende trigonometrischen Umformungen:
- $$ \cos(\alpha) \cdot \cos(\beta) = 1/2 \cdot \left[ \cos(\alpha - \beta)+ \cos(\alpha + \beta) \right],$$
- $$ \sin(\alpha) \cdot \sin(\beta) = 1/2 \cdot \left[ \cos(\alpha - \beta)- \cos(\alpha + \beta) \right],$$
- $$ \sin(\alpha) \cdot \cos(\beta) = 1/2 \cdot \left[ \sin(\alpha - \beta)+ \sin(\alpha + \beta) \right] \hspace{0.05cm}.$$
Fragebogen
Musterlösung
2.Mit $A_1 = A_2 = 2 V$ und $f_1 = f_2 = 5 kHz$ überlagern sich zwei dieser Cosinusschwingungen konstruktiv und zwei weitere heben sich vollständig auf. Es ergibt sich somit das folgende einfache Ergebnis:
$$ s(t) = 2\,{\rm V} \cdot \cos(2 \pi \cdot 20\,{\rm kHz} \cdot t) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} s(t = 50\,{\rm \mu s}) \hspace{0.15cm}\underline {= 2\,{\rm V}} \hspace{0.05cm}.$$
3. Richtig ist der erste Lösungsvorschlag. Bei phasensynchroner Demodulation ($Δϕ_T = 0$) erhält man für die Signale vor den beiden Tiefpässen mit $r(t) = s(t)$ entsprechend Teilaufgabe b):
$$b_1(t) = 2\,{\rm V} \cdot \cos(\omega_{\rm 20} \cdot t)\cdot 2 \cdot \cos(\omega_{\rm 25} \cdot t) = 2\,{\rm V} \cdot \cos(\omega_{\rm 5} \cdot t) + 2\,{\rm V} \cdot \cos(\omega_{\rm 45} \cdot t),$$
$$ b_2(t) = 2\,{\rm V} \cdot \cos(\omega_{\rm 20} \cdot t)\cdot 2 \cdot \sin(\omega_{\rm 25} \cdot t) = 2\,{\rm V} \cdot \sin(\omega_{\rm 5} \cdot t) + 2\,{\rm V} \cdot \sin(\omega_{\rm 45} \cdot t)\hspace{0.05cm}.$$
Nach Eliminierung der jeweiligen 45 kHz–Anteile ergibt sich somit $υ_1(t) = q_1(t)$ und $υ_2(t) = q_2(t)$.
4.Analog zur Teilaufgabe c) gilt nun:
$$ b_1(t) = 2\,{\rm V} \cdot \cos(\omega_{\rm 20} \cdot t)\cdot 2 \cdot \cos(\omega_{\rm 25} \cdot t+ \Delta \phi_{\rm T})=$$
$$ = 2\,{\rm V} \cdot \cos(\omega_{\rm 5} \cdot t + \Delta \phi_{\rm T}) + {(45 \,\rm kHz-Anteil )},$$
$$b_2(t)= 2\,{\rm V} \cdot \cos(\omega_{\rm 20} \cdot t)\cdot 2 \cdot \sin(\omega_{\rm 25} \cdot t+ \Delta \phi_{\rm T})=$$
$$ = 2\,{\rm V} \cdot \sin(\omega_{\rm 5} \cdot t + \Delta \phi_{\rm T}) + {(45 \,\rm kHz-Anteil )}\hspace{0.05cm}.$$
Die Sinkensignale $υ_1(t)$ und $υ_2(t)$ weisen bei dieser Konstellation gegenüber $q_1(t)$ und $q_2(t)$ Laufzeiten und damit Phasenverzerrungen auf. Diese gehören zur Klasse der linearen Verzerrungen.
5.Allgemein gilt für das Empfangssignal: $$r(t) = s(t) = q_1(t) \cdot \cos(\omega_{\rm T} \cdot t) + q_2(t) \cdot \sin(\omega_{\rm T} \cdot t) \hspace{0.05cm}.$$ Die Multiplikation mit den empfängerseitigen Trägersignalen $z_{1,E}(t)$ und $z_{2,E}(t)$ und die abschließende Bandbegrenzung führt zu den Sinkensignalen $$v_1(t) = \cos(\Delta \phi_{\rm T}) \cdot q_1(t) - \sin(\Delta \phi_{\rm T}) \cdot q_2(t),$$ $$ v_2(t) = \sin(\Delta \phi_{\rm T}) \cdot q_1(t) + \cos(\Delta \phi_{\rm T}) \cdot q_2(t) \hspace{0.05cm}.$$ Daraus ist zu ersehen: Bei einem Phasenversatz von $Δ_ϕT = 30°$ beinhaltet das Sinkensignal $υ_1(t)$ nicht nur das um $cos(30°) = 0.866$ gedämpfte Signal $q_1(t)$, sondern auch die in $q_2(t)$ enthaltene Frequenz $f_2$ (diese ist mit dem Faktor $sin(30°) = 0.5$ gewichtet). Es liegen somit nichtlineare Verzerrungen vor.