Aufgaben:Exercise 3.3: Sum of two Oscillations

• Return to book

Zwei verschiedene Besselspektren

Das äquivalente Tiefpass–Signal bei Phasenmodulation lautet

$$ s_{\rm TP}(t) = {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}K_{\rm PM}\hspace{0.05cm}\cdot \hspace{0.05cm}q(t) }\hspace{0.05cm},$$

wenn eine Normierung auf die Trägeramplitude vorgenommen wird ($A_{\rm T = 1}$). Die Modulatorkonstante wird in der gesamten Aufgabe zu $K_{PM} = \rm 1/V$ angenommen.

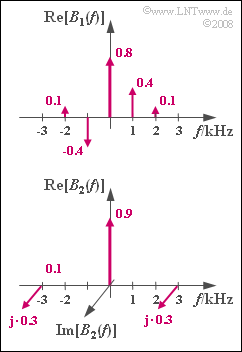
Die obere Grafik zeigt die dazugehörige Spektralfunktion $B_1(f)$, wenn das Quellensignal

$$q_1(t) = 0.9\,{\rm V} \cdot \sin(2 \pi \cdot 1\,{\rm kHz} \cdot t)$$

anliegt. Die Gewichte der Bessel-Diraclinien ergeben sich mit $η_1 = 0.9$ wie folgt:

$${\rm J}_0 (0.9) = 0.808 \approx 0.8,\hspace{1cm} {\rm J}_1 (0.9) = 0.406 \approx 0.4,$$

$${\rm J}_2 (0.9) = 0.095 \approx 0.1,\hspace{1cm} {\rm J}_3 (0.9) \approx {\rm J}_4 (0.9) \approx\ \text{ ...} \ \approx 0 \hspace{0.05cm}.$$

Verwenden Sie zur Vereinfachung der Berechnungen die in der Skizze angegebenen Näherungswerte.

Die Besselfunktion $B_2(f)$ ergibt sich für das Quellensignal

$$q_2(t) = 0.65\,{\rm V} \cdot \cos(2 \pi \cdot 3\,{\rm kHz} \cdot t)$$

Die Zahlenwerte der Diraclinien erhält man hier aus folgender Angabe:

$${\rm J}_0 (0.65) = 0.897 \approx 0.9,\hspace{0.3cm}{\rm J}_1 (0.65) = 0.308 \approx 0.3, \hspace{0.3cm}{\rm J}_2 (0.65) = 0.051 \approx 0\hspace{0.05cm}.$$

Aus der Grafik ist zu erkennen, dass aufgrund des cosinusförmigen Quellensignals $q_2(t)$ und des cosinusförmigen Trägersignals $z(t)$ die Spektrallinien bei $±3 \ \rm kHz$ jeweils positiv–imaginär sind.

Im Rahmen dieser Aufgabe soll nun der Fall untersucht werden, dass das Quellensignal

$$q(t) = q_1(t) + q_2(t)$$

am Eingang des Phasenmodulators anliegt. Zu erwähnen ist, dass $|q(t)| < q_{max} = 1.45 \ \rm V$ gilt. Dieser Maximalwert ist etwas kleiner als die Summe $A_1 + A_2$ der Einzelamplituden, wenn eine Sinus– und eine Cosinusfunktion mit den gegebenen Amplituden aufaddiert werden.

Im Fragebogen bezeichnen

• $S_{\rm TP}(f)$ die Spektralfunktion des äquivalenten TP–Signals,
• $S_+(f)$ die Spektralfunktionen des analytischem Signals,

jeweils unter der Annahme, dass $q(t) = q_1(t) + q_2(t)$ anliegt und die Trägerfrequenz $f_{\rm T} = 100 \ \rm kHz$ beträgt.

Hinweise:

• Die Aufgabe gehört zum Kapitel Phasenmodulation.
• Bezug genommen wird insbesondere auf die Seite Äquivalentes Tiefpass-Signal bei Phasenmodulation.
• Die Werte der Besselfunktionen findet man in Formelsammlungen in tabellarischer Form.
• Sie können zur Lösung dieser Aufgabe auch das Interaktionsmodul Werte der Besselfunktion erster Art und n–ter Ordnung nutzen.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Welche geometrische Figur beschreibt die angegebene Ortskurve $s_{\rm TP}(t)$?

	Die Ortskurve ist eine Ellipse.
	Die Ortskurve ist ein Kreis.
	Die Ortskurve ist näherungsweise ein Halbkreis.
	Die Ortskurve ist ein Kreisbogen, etwa mit Öffnungswinkel $90^\circ$.

2

Berechnen Sie die Spektralfunktion $S_{\rm TP}(f)$. Zwischen welchen Frequenzen $f_{\rm min}$ und $f_{\rm max}$ liegen Spektrallinien?

$f_{\rm min} \ = \ $ $\ \rm kHz$

$f_{\rm max} \ = \ $ $\ \rm kHz$

3

Berechnen Sie das Gewicht der Diracfunktion bei $f = 0$.

${\rm Re}[S_{\rm TP}(f = 0)] \ = \ $

${\rm Im}[S_{\rm TP}(f = 0)] \ = \ $

4

Berechnen Sie das Gewicht der Diracfunktion bei $f = 1\ \rm kHz$.

${\rm Re}[S_{\rm TP}(f = 1 \ \rm kHz)] \ = \ $

${\rm Im}[S_{\rm TP}(f = 1 \ \rm kHz)] \ = \ $

5

Berechnen Sie das Gewicht der $S_+(f)$–Diracfunktion bei $f = 98 \ \rm kHz$.

${\rm Re}[S_{\rm +}(f = 98 \ \rm kHz)] \ = \ $

${\rm Im}[S_{\rm +}(f = 98 \ \rm kHz)] \ = \ $

Musterlösung

Solution

1.Bei Winkelmodulation bewegt sich der komplexe Zeiger $s_{TP}(t)$ stets auf einem Kreisbogen, dessen Öffnungswinkel $2 · K_{PM} · q_{max} = 2.9 (≈ π = 180 °)$ beträgt. Richtig ist somit die dritte Alternative.

2. Es gilt $S_{TP}(f) = B_1(f) ∗ B_2(f)$. Da $B_1(f)$ auf Frequenzen $|f| ≤ 2 kHz$ und $B_2(f)$ auf den Bereich $±3 kHz$ begrenzt sind, ist das Faltungsprodukt auf $|f| ≤ 5$ kHz beschränkt: $f_{min} = –5 kHz$, $f_{max} = 5 kHz$.

3.Das Faltungsprodukt für $f = 0$ ergibt sich durch Multiplikation von $B_1(f)$ mit $B_2(f)$ und anschließender Summation. Nur für $f = 0$ sind sowohl $B_1(f)$ als auch $B_2(f)$ von Null verschieden. Damit erhält man: $$ S_{\rm TP}(f = 0) = B_{1}(f = 0) \cdot B_{2}(f = 0)= 0.8 \cdot 0.9 \hspace{0.15cm}\underline {= 0.72}\hspace{0.2cm}{\rm (rein \hspace{0.15cm} reell)} \hspace{0.05cm}.$$

4. Nun muss vor der Multiplikation und Summation noch eine Frequenzverschiebung von $B_2(f)$ nach rechts – oder von $B_1(f)$ nach links – um 1 kHz erfolgen. Somit erhält man: $$S_{\rm TP}(f = 1\,{\rm kHz}) = B_{1}(f = -2\,{\rm kHz}) \cdot B_{2}(f = 3\,{\rm kHz}) +$$ $$ + B_{1}(f = 1\,{\rm kHz}) \cdot B_{2}(f = 0)=$$ $$ = 0.1 \cdot {\rm j} \cdot 0.3 + 0.4 \cdot 0.9\hspace{0.15cm} = 0.36 + {\rm j} \cdot 0.03$$ $$\Rightarrow \hspace{0.3cm} {\rm Re}[S_{\rm TP}(f = 1\,{\rm kHz})] \hspace{0.15cm}\underline {= 0.36} \hspace{0.05cm},\hspace{0.3cm} {\rm Im}[S_{\rm TP}(f = 1\,{\rm kHz})] \hspace{0.15cm}\underline {= 0.03} \hspace{0.05cm}.$$

5. Die Diraclinie $S_+(f = 98 kHz)$ entspricht der $S_{TP}(f)$–Linie bei $f = –2 kHz$. Diese ist $$S_{\rm TP}(f = -2\,{\rm kHz}) = B_{1}(f = -2\,{\rm kHz}) \cdot B_{2}(f = 0) +$$ $$ + B_{1}(f = 1\,{\rm kHz}) \cdot B_{2}(f = -3\,{\rm kHz})=$$ $$= 0.1 \cdot 0.9 + 0.4 \cdot {\rm j} \cdot 0.3 \hspace{0.15cm}= 0.09 + {\rm j} \cdot 0.12$$ $$\Rightarrow \hspace{0.3cm} {\rm Re}[S_{\rm +}(f = 98\,{\rm kHz})] \hspace{0.15cm}\underline {= 0.09} \hspace{0.05cm}, \hspace{0.3cm} {\rm Im}[S_{\rm +}(f = 98\,{\rm kHz})] \hspace{0.15cm}\underline {= 0.12} \hspace{0.05cm}.$$