Aufgaben:Exercise 3.9: Circular Arc and Parabola

• Return to book

Kreisbogen und Parabel

Wir betrachten hier die Frequenzmodulation eines cosinusförmigen Quellensignals

$$q(t) = A_{\rm N} \cdot \cos(2 \pi \cdot f_{\rm N} \cdot t )$$

mit der Amplitude $A_{\rm N} = 1 \ \rm V$ und der Frequenz $f_{\rm N} = 5 \ \rm kHz$. Der Modulationsindex (Phasenhub) beträgt $η = 2.4$. Das zugehörige TP–Signal lautet bei normierter Trägeramplitude ($A_{\rm T} = 1$):

$$ s_{\rm TP}(t) = \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n\hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm N} \hspace{0.05cm}\cdot \hspace{0.05cm} t}.$$

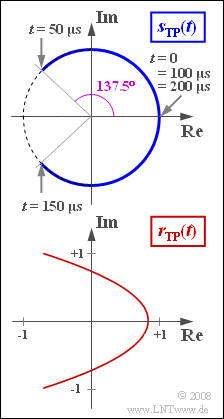
Dieses beschreibt einen Kreisbogen. Innerhalb der Periodendauer $T_{\rm N} = 1/f_{\rm N} = 200 \ \rm μs$ ergeben sich folgende Phasenwinkel:

$$ \phi(0) = 0, \hspace{0.2cm}\phi(0.25 \cdot T_{\rm N}) = \eta, \hspace{0.2cm}\phi(0.5 \cdot T_{\rm N})= 0,\hspace{0.2cm} \phi(0.75 \cdot T_{\rm N})= -\eta,\hspace{0.2cm}\phi(T_{\rm N})= 0.$$

• Die erforderliche Kanalbandbreite zur Übertragung dieses Signals ist theoretisch unendlich groß.
• Ist die Bandbreite jedoch begrenzt, zum Beispiel auf $B_{\rm K} = 25 \ \rm kHz$, so kann das äquivalente TP–Signal des Empfangssignals wie folgt beschrieben werden:

$$r_{\rm TP}(t) = \sum_{n = - 2}^{+2}{\rm J}_n (\eta) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n\hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm N} \hspace{0.05cm}\cdot \hspace{0.05cm} t}.$$

In diesem Fall ergibt sich eine parabelförmige Ortskurve

$$ y^2 + a \cdot x + b = 0,$$

die in dieser Aufgabe analysiert werden soll.

Hinweise:

• Die Aufgabe gehört zum Kapitel Frequenzmodulation.
• Bezug genommen wird aber auch auf das Kapitel Phasenmodulation und insbesondere auf den Abschnitt Signalverläufe bei Frequenzmodulation.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Gehen Sie bei der Berechnung von folgenden Werten der Besselfunktion aus:

$${\rm J}_0 (2.4) \approx 0, \hspace{0.2cm}{\rm J}_1 (2.4) = -{\rm J}_{-1} (2.4)\approx 0.52, \hspace{0.2cm}{\rm J}_2 (2.4) = {\rm J}_{-2} (2.4)\approx 0.43.$$

Fragebogen

1

Wie groß ist die Modulatorkonstante $K_{\rm FM}$?

$K_{\rm FM} \ = \ $ $\ \rm (Vs)^{-1}$

2

Berechnen Sie den Realteil $x(t) = {\rm Re}[r_{\rm TP}(t)]$ des äquivalenten TP-Signals und geben Sie dessen Maximum und Minimum an.

$x_{\rm max} \ = \ $

$x_{\rm min} \ = \ $

3

Wie groß ist das Maximum und Minimum des Imaginärteils $y(t) = {\rm Im}[r_{\rm TP}(t)]$?

$y_{\rm max} \ = \ $

$y_{\rm min} \ = \ $

4

Welche Phasenwerte ergeben sich bei allen Vielfachen von $T_{\rm N}/2$?

$ϕ(t = n · T_{\rm N}/2) \ = \ $ $\ \rm Grad$

5

Wie groß ist der maximale Phasenwinkel $ϕ_{\rm max}$? Interpretieren Sie das Ergebnis.

$ϕ_{max} \ = \ $ $\ \rm Grad$

6

Zeigen Sie, dass man die Ortskurve in der Form $y^2 + a · x + b = 0$ angeben kann. Bestimmen Sie die Parabelparameter $a$ und $b$.

$a\ = \ $

$b\ = \ $

Musterlösung

Solution

(1)  Bei Frequenzmodulation eines Cosinussignals gilt für den Modulationsindex:

$$ \eta = \frac{K_{\rm FM} \cdot A_{\rm N}}{ \omega_{\rm N}} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} K_{\rm FM} = \frac{2 \pi \cdot f_{\rm N }\cdot \eta}{ A_{\rm N}} = \frac{2 \pi \cdot 5 \cdot 10^3 \,{\rm Hz}\cdot 2.4}{ 1\,{\rm V}} \hspace{0.15cm}\underline {\approx 7.54 }\cdot 10^4 \,\,{\rm V}^{-1}{\rm s}^{-1}\hspace{0.05cm}.$$

(2)  Die angegebene Gleichung für das äquivalente TP–Signal lautet in ausgeschriebener Form mit der Abkürzung $γ = ω_{\rm N} · t$ unter Berücksichtigung von ${\rm J}_{–1} = –{\rm J}_1$ und ${\rm J}_{–2} = {\rm J}_2$:

$$r_{\rm TP}(t) = {\rm J}_0 + \left[ {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \gamma} - {\rm e}^{\hspace{0.05cm}{-\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \gamma} \right]\cdot {\rm J}_1 \hspace{0.27cm} +\left[ {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\gamma} + {\rm e}^{\hspace{0.05cm}{-\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\gamma} \right]\cdot {\rm J}_2 = {\rm J}_0 + 2 \cdot {\rm j} \cdot {\rm J}_1 \cdot \sin (\gamma)+ 2 \cdot {\rm J}_2 \cdot \cos (2\gamma)\hspace{0.05cm} .$$

Somit ergibt sich für den Realteil allgemein bzw. für $η = 2.4$, das heißt ${\rm J}_0 = 0$ und ${\rm J}_2 = 0.43$:

$$ x(t) = {\rm J}_0 + 2 \cdot {\rm J}_2 \cdot \cos (2 \omega_{\rm N} t ) = 2 \cdot {\rm J}_2 \cdot \cos (2 \omega_{\rm N} t ) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} x_{\rm max} = 2 \cdot {\rm J}_2\hspace{0.15cm}\underline { = 0.86}, \hspace{0.3cm} x_{\rm min} = -x_{\rm max} \hspace{0.15cm}\underline {= -0.86}\hspace{0.05cm}.$$

(3)  Entsprechend dem Ergebnis der Teilaufgabe (2) erhält man für den Imaginärteil (${\rm J}_1 = 0.52$):

$$y(t) = 2 \cdot {\rm J}_1 \cdot \sin ( \omega_{\rm N} t )\hspace{0.3cm}\Rightarrow \hspace{0.3cm} y_{\rm max} =2 \cdot {\rm J}_1\hspace{0.15cm}\underline { = 1.04}\hspace{0.05cm}, \hspace{0.3cm} y_{\rm min} = -y_{\rm max}\hspace{0.15cm}\underline { = -1.04}\hspace{0.05cm}.$$

(4)  Der Imaginärteil ist zu diesen Zeitpunkten jeweils 0 und damit auch die Phasenfunktion:   $ϕ(t = n · T_{\rm N}/2)\hspace{0.15cm}\underline{= 0}$ . Diesen Sachverhalt erkennt man auch aus der Skizze auf der Angabenseite.

(5)  Aus der Skizze ist bereits zu erkennen, dass der Phasenwinkel beispielsweise für $t = T_{\rm N}/4$ seinen Maximalwert erreicht. Dieser kann mit $y_{\rm max} = 1.04$ und $x_{{\rm N}min} = -0.86$ wie folgt berechnet werden:

$$\phi_{\rm max} = \arctan \frac{y_{\rm max}}{x_{\rm min}} = \arctan (-1.21) = 180^\circ - 50.4^\circ \hspace{0.15cm}\underline {= 129.6^\circ} \hspace{0.05cm}.$$

• Ohne Bandbegrenzung würde sich hier der Phasenwinkel $ϕ(t = T_{\rm N}/4) = η = 2.4 = 137.5^\circ$ ergeben.
• Die maximale Abweichung des Sinkensignals vom Quellensignal tritt somit z.B. zur Zeit $t = T_{\rm N}/4$ auf.

(6)  Mit $γ = ω_{\rm N} · t$ und $\cos(2γ) = 1 - 2 · \cos^2(γ)$ kann für Real– und Imaginärteil geschrieben werden:

$$x = {\rm J}_0 + 4 \cdot {\rm J}_2 \cdot \cos^2 (\gamma) - 2 \cdot {\rm J}_2\hspace{0.05cm},\hspace{0.3cm} y = 2 \cdot {\rm J}_1 \cdot \sin (\gamma) \hspace{0.05cm}.$$

Parabelverlauf

Diese Gleichungen können wie folgt umgeformt werden:

$$\cos^2 (\gamma) =\frac{x-{\rm J}_0 + 2 \cdot {\rm J}_2 }{4 \cdot {\rm J}_2} \hspace{0.05cm},\hspace{0.3cm} \sin^2 (\gamma) = \frac{y^2 }{4 \cdot {\rm J}_1^2}$$

$$\Rightarrow \hspace{0.3cm} \frac{y^2 }{4 \cdot {\rm J}_1^2} + \frac{x-{\rm J}_0 + 2 \cdot {\rm J}_2 }{4 \cdot {\rm J}_2} =1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {y^2 } + \frac{{\rm J}_1^2}{ {\rm J}_2} \cdot x + {{\rm J}_1^2} \cdot \left ( 2 - \frac{{\rm J}_0}{ {\rm J}_2} \right ) =0\hspace{0.05cm}.$$

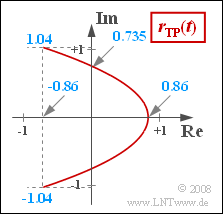
Damit lauten die Parabelparameter für $ {\rm J}_0 = 0$:

$$a = \frac{{\rm J}_1^2}{ {\rm J}_2} \hspace{0.15cm}\underline {\approx 0.629}, \hspace{0.3cm} b = 2 \cdot {\rm J}_1^2 \hspace{0.15cm}\underline {\approx 0.541} \hspace{0.05cm}.$$

• Zur Kontrolle verwenden wir $y = 0$:   $ x_{\rm max} = {b}/{a} = 2 \cdot {\rm J}_2 = 0.86 \hspace{0.05cm}.$
• Die Werte bei $x = 0$ sind somit:   $y_0 = \pm \sqrt{2} \cdot {\rm J}_1 \approx 0.735 \hspace{0.05cm}.$