Aufgaben:Exercise 3.11: Pre-Emphase and De-Emphase

• Return to book

Realisierung einer Preemphase

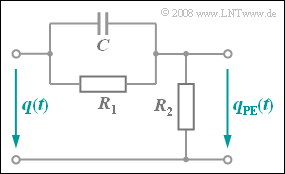
Bei der Sprach– und Tonsignalübertragung wird das Signalfrequenzband vor dem FM–Modulator über ein RC–Hochpassglied gemäß der Skizze vorverzerrt. Man bezeichnet diese Maßnahme als Preemphase (PE).

Der Amplitudengang des Preemphase–Netzwerks lautet

• mit den beiden Grenzfrequenzen $f_{\rm G1} = (2π · R_1 · C)^{–1}$ und $f_{\rm G2} = f_{G1}/α_0$, sowie
• dem Gleichsignalübertragungsfaktor $α_0 = R_2/(R_1 + R_2)$r:

$$ |H_{\rm PE} (f)| = \alpha_0 \cdot \sqrt{\frac{1 + (f/f_{\rm G1})^2}{1 + (f/f_{\rm G2})^2}} \hspace{0.05cm}.$$

Für den praktischen Betrieb kann man davon ausgehen, dass die maximale Nachrichtenfrequenz $f_{\rm N}$ sehr viel kleiner als $f_{\rm G2}$ ist. Berücksichtigt man weiter, dass der Gleichsignalübertragungsfaktor $α_0$ durch eine Verstärkung um $α$ verändert werden kann, so ist im Weiteren von folgendem Preemphase–Frequenzgang auszugehen ($f_{\rm G} = f_{\rm G1} = 3 \ \rm kHz$):

$$|H_{\rm PE} (f)| \approx \alpha \cdot \sqrt{{1 + \left({f}/{f_{\rm G}}\right)^2}} \hspace{0.05cm}.$$

Mit diesem Netzwerk lautet der Frequenzhub $Δf_{\rm A}$ in Abhängigkeit der Nachrichtenfrequenz $f_{\rm N}$:

$$ \Delta f_{\rm A} (f_{\rm N}) = \Delta f_{\rm A, \hspace{0.08cm}min} \cdot \sqrt{{1 + \left({f_{\rm N}}/{f_{\rm G}}\right)^2}} \hspace{0.05cm}.$$

Hierbei ist $Δf_\text{A, min}$ der Frequenzhub für sehr kleine Frequenzen ($f_{\rm N} → 0$). Dieser Parameter ist so zu wählen, dass der maximale Frequenzhub $Δf_\text{A, max}$ nicht größer wird als $45 \ \rm kHz$.

Um das Nutzsignal nicht zu verfälschen, muss diese Vorverzerrung durch ein Deemphase–Netzwerk beim Empfänger wieder ausgeglichen werden. Ziel und Zweck von Preemphase/Deemphase ist es allein, die Abhängigkeit des Signal–zu–Rausch–Leistungsverhältnisses von der Signalfrequenz zu vermindern.

In dieser Aufgabe werden folgende Größen verwendet:

• Sinken–SNR bei Zweiseitenband-Amplitudenmodulation (ZSB–AM):

$$\rho_{{\rm AM} } = \frac{P_{\rm S}}{N_0 \cdot f_{\rm N} } = \xi\hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{{\rm AM} } = 10 \cdot {\rm lg} \hspace{0.15cm}\xi \hspace{0.05cm},$$

• Sinken–SNR und Störabstandsgewinn bei Frequenzmodulation (FM) ohne Preemphase/Deemphase:

$$ \rho_{\rm FM} = {3}/{2 } \cdot \eta^2 \cdot \rho_{\rm AM } \hspace{0.3cm}\Rightarrow \hspace{0.3cm} G_{\rm FM} = 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{\rm FM} - 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{\rm AM}= 10 \cdot {\rm lg} \hspace{0.15cm}{3}/{2 } \cdot \eta^2 \hspace{0.05cm},$$

• Sinken–SNR und Störabstandsgewinn bei Frequenzmodulation (FM) durch Preemphase/Deemphase:

$$ \rho_{\rm DE} = \frac{(f_{\rm N}/f_{\rm G})^3}{3 \cdot (f_{\rm N}/f_{\rm G} - \arctan (f_{\rm N}/f_{\rm G}) } \hspace{0.3cm}\Rightarrow \hspace{0.3cm} G_{\rm DE} = 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{\rm DE} - 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{\rm FM}\hspace{0.05cm}$$

Hinweise:

• Die Aufgabe gehört zum Kapitel Rauscheinfluss bei Winkelmodulation.
• Bezug genommen wirdinsbesondere auf den Abschnitt Preemphase und Deemphase.
• Gehen Sie in der gesamten Aufgabe von einem Nachrichtensignal aus, das Frequenzen bis einschließlich $B_{\rm NF}= 9 \ \rm kHz$ beinhaltet.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Geben Sie eine mögliche Realisierung des Deemphase–Netzwerks $H_{\rm DE}(f)$ an. Welche der folgenden Aussagen sind richtig?

	$H_{\rm DE}(f)$ ist ein Tiefpass erster Ordnung.
	$H_{\rm DE}(f)$ ist ein Hochpass erster Ordnung.
	$H_{\rm DE}(f)$ ist ein Bandpass.
	Zusätzlich muss der Faktor $α$ korrigiert werden.

2

Wie groß ist der Störabstandsgewinn $G_{FM}$ der herkömmlichen FM gegenüber AM bei den genannten Nachrichtenfrequenzen $ f_{\rm N}$?

$ f_{\rm N} = 9 \ \rm kHz\text{:} \hspace{0.2cm} G_{\rm FM} \ = \ $ $\ \rm dB$

$ f_{\rm N} = 3 \ \rm kHz\text{:} \hspace{0.2cm} G_{\rm FM} \ = \ $ $\ \rm dB$

$ f_{\rm N} = 1 \ \rm kHz\text{:} \hspace{0.2cm} G_{\rm FM} \ = \ $ $\ \rm dB$

3

Wie groß ist $Δf_\text{A, min}$ mit $Δf_\text{A, max} = 45 \ \rm kHz$ und $B_{\rm NF} = f_\text{N, max}= 9 \ \rm kHz$ zu wählen?

$Δf_\text{A, min} \ = \ $ $\ \rm kHz$

4

Welcher zusätzliche Gewinn ist durch Preemphase/Deemphase zu erzielen?

$ f_{\rm N} = 9 \ \rm kHz\text{:} \hspace{0.2cm} G_{\rm DE} \ = \ $ $\ \rm dB$

$ f_{\rm N} = 3 \ \rm kHz\text{:} \hspace{0.2cm} G_{\rm DE} \ = \ $ $\ \rm dB$

$ f_{\rm N} = 1 \ \rm kHz\text{:} \hspace{0.2cm} G_{\rm DE} \ = \ $ $\ \rm dB$

Musterlösung

Solution

(1)  Richtig sind der erste und der letzte Lösungsvorschlag:

• Der Betragsfrequenzgang des Deemphase–Netzwerks ist wie folgt festgelegt:

$$ |H_{\rm DE} (f)| = \frac{1}{|H_{\rm PE} (f)|}= \frac{1}{\alpha}\cdot \frac{1}{\sqrt{1 + (f/f_{\rm G})^2}} \hspace{0.05cm}.$$

• Der Frequenzgang eines einfachen RC–Tiefpasses – auch bekannt als Tiefpass erster Ordnung – lautet:

$$ H_{\rm RC-TP} (f) = \frac{1}{{1 + {\rm j}\cdot f/f_{\rm G}}} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} |H_{\rm RC-TP} (f)| = \frac{1}{\sqrt{1 + (f/f_{\rm G})^2}}\hspace{0.05cm}.$$

(2)  Die Frequenzmodulation (FM) ist auf die maximale Signalfrequenz $B_{\rm NF} = f_\text{N, max}= 9 \ \rm kHz$ ausgelegt, mit der der (maximale) Frequenzhub $Δf_{\rm A} = 45\ \rm kHz$ betragen soll. Daraus folgt für den Modulationsindex:

$$ \eta = \frac{\Delta f_{\rm A}}{f_{\rm N} } = 5 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} G_{\rm FM} (f_{\rm N} = 9\,{\rm kHz}) = 10 \cdot {\rm lg} \hspace{0.15cm}(1.5 \cdot 5^2) \hspace{0.15cm}\underline {\approx 15.74\,{\rm dB}} \hspace{0.05cm}.$$

Mit der Nachrichtenfrequenz $ f_{\rm N} = 3 \ \rm kHz$ ergibt sich ein um den Faktor $3$ größerer Modulationsindex und damit ein um den Faktor $10 · \lg \ 9 = 9.54 \ \rm dB$ größerer Störabstand:

$$G_{\rm FM} (f_{\rm N} = 3\,{\rm kHz}) = 10 \cdot {\rm lg} \hspace{0.15cm}(1.5 \cdot 15^2) \hspace{0.15cm}\underline {\approx 25.28\,{\rm dB}} \hspace{0.05cm}.$$

Ein weiterer Zugewinn ergibt sich durch den Übergang von $3\ \rm kHz$ auf $1\ \rm kHz$:

$$G_{\rm FM} (f_{\rm N} = 1\,{\rm kHz}) = 25.28\,{\rm dB} + 9.54\,{\rm dB}\hspace{0.15cm}\underline {= 34.82\,{\rm dB}} \hspace{0.05cm}.$$

(3)  Der maximale Frequenzhub ergibt sich für $f_{\rm N} = B_{\rm NF}$. Daraus folgt mit $f_{\rm G} = 3 \ \rm kHz$ und $B_{\rm NF} = 9 \ \rm kHz$:

$$\Delta f_{\rm A} (B_{\rm NF}) = \Delta f_{\rm A, \hspace{0.08cm}min} \cdot \sqrt{{1 + \left(\frac{B_{\rm NF}}{f_{\rm G}}\right)^2}} = \sqrt {10} \cdot \Delta f_{\rm A, \hspace{0.08cm}min}= \Delta f_{\rm A, \hspace{0.08cm}max} = 45\,{\rm kHz}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \Delta f_{\rm A, \hspace{0.08cm}min} = \frac{45\,{\rm kHz}}{\sqrt {10}}\hspace{0.15cm}\underline {\approx 14.23\,{\rm kHz}}\hspace{0.05cm}.$$

(4)  Mit der angegebenen Formel erhält man folgende Gewinne:

$$G_{\rm DE} (f_{\rm N} = 9\,{\rm kHz}) = 10 \cdot {\rm lg}\hspace{0.15cm} \frac{(f_{\rm N}/f_{\rm G})^3}{3 \cdot (f_{\rm N}/f_{\rm G} - \arctan (f_{\rm N}/f_{\rm G}) }= 10 \cdot {\rm lg}\hspace{0.15cm} \frac{3^3}{3 \cdot (3 - 1.249) }\hspace{0.15cm}\underline {\approx 7.1\,{\rm dB}}\hspace{0.05cm},$$

$$ G_{\rm DE} (f_{\rm N} = 3\,{\rm kHz}) = 10 \cdot {\rm lg}\hspace{0.15cm} \frac{1^3}{3 \cdot (1 - \pi/4) }\hspace{0.15cm}\underline {\approx 1.9\,{\rm dB}}\hspace{0.05cm},$$

$$G_{\rm DE} (f_{\rm N} = 1\,{\rm kHz}) = 10 \cdot {\rm lg}\hspace{0.15cm} \frac{(1/3)^3}{3 \cdot (1/3 - 0.322) }\hspace{0.15cm}\underline {\approx 0.28\,{\rm dB}}\hspace{0.05cm}.$$