Difference between revisions of "Aufgaben:Exercise 5.2Z: About PN Modulation"
m (Guenter verschob die Seite 5.2Z PN–Modulation nach 5.2Z Zur PN–Modulation) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
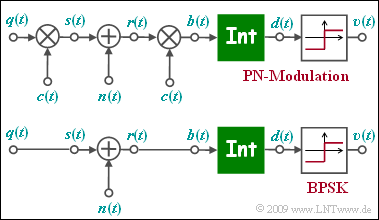
| − | [[File:P_ID1871__Mod_Z_5_2.png|right|]] | + | [[File:P_ID1871__Mod_Z_5_2.png|right|frame|Modelle von PN–Modulation (oben) und BPSK (unten)]] |
| − | Die Grafik zeigt das Ersatzschaltbild der PN–Modulation (''engl. Direct Sequence Spread Spectrum'', abgekürzt DS–SS) im äquivalenten Tiefpassbereich, wobei AWGN–Rauschen $n(t)$ zugrunde liegt. Darunter dargestellt ist das TP–Modell der binären Phasenmodulation (BPSK). Das Tiefpass–Sendesignal $s(t)$ ist aus Gründen einheitlicher Darstellung gleich dem rechteckförmigen Quellensignal $q(t) | + | Die Grafik zeigt das Ersatzschaltbild der PN–Modulation (''engl. Direct Sequence Spread Spectrum'', abgekürzt DS–SS) im äquivalenten Tiefpassbereich, wobei AWGN–Rauschen $n(t)$ zugrunde liegt. Darunter dargestellt ist das TP–Modell der binären Phasenmodulation (BPSK). |
| − | $$d (\nu T) = \frac{1}{T} \cdot \hspace{-0.1cm} \int_{(\nu -1 )T }^{\nu T} \hspace{-0.3cm} b (t )\hspace{0.1cm} {\rm d}t \hspace{0.05cm}.$$ | + | |
| − | Die beiden Modelle unterscheiden sich durch die Multiplikation mit dem | + | Das Tiefpass–Sendesignal $s(t)$ ist aus Gründen einheitlicher Darstellung gleich dem rechteckförmigen Quellensignal $q(t) ∈ \{+1, –1\}$ mit Rechteckdauer $T$ gesetzt ist. Die Funktion des Integrators kann wie folgt beschrieben werden: |
| + | :$$d (\nu T) = \frac{1}{T} \cdot \hspace{-0.1cm} \int_{(\nu -1 )T }^{\nu T} \hspace{-0.3cm} b (t )\hspace{0.1cm} {\rm d}t \hspace{0.05cm}.$$ | ||
| + | |||
| + | Die beiden Modelle unterscheiden sich durch die Multiplikation mit dem $±1$–Spreizsignal $c(t)$ bei Sender und Empfänger, wobei von $c(t)$ lediglich der Spreizgrad $J$ bekannt ist. | ||
Zu untersuchen ist, ob sich das untere BPSK–Modell auch bei PN–Modulation anwenden lässt und ob die BPSK–Fehlerwahrscheinlichkeit | Zu untersuchen ist, ob sich das untere BPSK–Modell auch bei PN–Modulation anwenden lässt und ob die BPSK–Fehlerwahrscheinlichkeit | ||
| − | $$p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt { | + | :$$p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt { {2 \cdot E_{\rm B}}/{N_{\rm 0}} } \hspace{0.05cm} \right )$$ |
auch für die PN–Modulation gültig ist, bzw. wie die angegebene Gleichung zu modifizieren ist. | auch für die PN–Modulation gültig ist, bzw. wie die angegebene Gleichung zu modifizieren ist. | ||
| − | '' | + | |
| + | ''Hinweise:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/PN–Modulation|PN–Modulation]]. | ||
| + | *Für die Lösung dieser Aufgabe ist die Angabe der spezifischen Spreizfolge (M–Sequenz oder Walsh–Funktion) nicht von Bedeutung. | ||
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| + | |||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Welche Detektionssignalwerte sind bei BPSK | + | {Welche Detektionssignalwerte sind bei BPSK (im rauschfreien Fall) möglich? |
|type="[]"} | |type="[]"} | ||
| − | - $d(νT)$ | + | - $d(νT)$ kann gaußverteilt sein. |
| − | - $d(νT)$ kann die Werte +1, 0 und | + | - $d(νT)$ kann die Werte $+1$, $0$ und $-1$ annehmen. |
| − | + Es sind nur die Werte $d(νT) = +1$ und $d(νT) = | + | + Es sind nur die Werte $d(νT) = +1$ und $d(νT) = -1$ möglich. |
| − | {Welche Werte sind bei PN–Modulation im rauschfreien Fall möglich? | + | {Welche Werte sind bei PN–Modulation (im rauschfreien) Fall möglich? |
|type="[]"} | |type="[]"} | ||
| − | - $d(νT)$ | + | - $d(νT)$ kann gaußverteilt sein. |
| − | - $d(νT)$ kann die Werte +1, 0 und | + | - $d(νT)$ kann die Werte $+1$, $0$ und $-1$ annehmen. |
| − | + Es sind nur die Werte $d(νT) = +1$ und $d(νT) = | + | + Es sind nur die Werte $d(νT) = +1$ und $d(νT) = -1$ möglich. |
{Welche Modifikation muss am BPSK–Modell vorgenommen werden, damit es auch für die PN–Modulation anwendbar ist? | {Welche Modifikation muss am BPSK–Modell vorgenommen werden, damit es auch für die PN–Modulation anwendbar ist? | ||
|type="[]"} | |type="[]"} | ||
| − | + Das Rauschen n(t) muss durch $n'(t) = n(t) · c(t)$ ersetzt werden. | + | + Das Rauschen $n(t)$ muss durch $n'(t) = n(t) · c(t)$ ersetzt werden. |
| − | - Die Integration muss nun über J · T erfolgen. | + | - Die Integration muss nun über $J · T$ erfolgen. |
| − | - Die Rauschleistung $σ_n^2$ muss um den Faktor J vermindert werden. | + | - Die Rauschleistung $σ_n^2$ muss um den Faktor $J$ vermindert werden. |
| − | {Welche Bitfehlerwahrscheinlichkeit $p_B$ ergibt sich für $10 lg | + | {Welche Bitfehlerwahrscheinlichkeit $p_B$ ergibt sich für $10 \lg \ (E_{\rm B}/N_0) = 6\ \rm dB$ bei PN–Modulation? |
| + | ''Hinweis.'' Bei BPSK gilt in diesem Fall: $p_{\rm B} ≈ 2.3 · 10^{–3}$. | ||
|type="[]"} | |type="[]"} | ||
| − | - Je größer J gewählt wird, desto kleiner ist $ | + | - Je größer $J$ gewählt wird, desto kleiner ist $p_{\rm B}$. |
| − | - Je größer J gewählt wird, desto größer ist $ | + | - Je größer $J$ gewählt wird, desto größer ist $p_{\rm B}$. |
| − | + Es ergibt sich unabhängig von J stets der Wert $2.3 · 10^{–3}$. | + | + Es ergibt sich unabhängig von $J$ stets der Wert $p_{\rm B} ≈ 2.3 · 10^{–3}$. |
</quiz> | </quiz> | ||
Revision as of 10:35, 1 August 2017
Die Grafik zeigt das Ersatzschaltbild der PN–Modulation (engl. Direct Sequence Spread Spectrum, abgekürzt DS–SS) im äquivalenten Tiefpassbereich, wobei AWGN–Rauschen $n(t)$ zugrunde liegt. Darunter dargestellt ist das TP–Modell der binären Phasenmodulation (BPSK).
Das Tiefpass–Sendesignal $s(t)$ ist aus Gründen einheitlicher Darstellung gleich dem rechteckförmigen Quellensignal $q(t) ∈ \{+1, –1\}$ mit Rechteckdauer $T$ gesetzt ist. Die Funktion des Integrators kann wie folgt beschrieben werden:
- $$d (\nu T) = \frac{1}{T} \cdot \hspace{-0.1cm} \int_{(\nu -1 )T }^{\nu T} \hspace{-0.3cm} b (t )\hspace{0.1cm} {\rm d}t \hspace{0.05cm}.$$
Die beiden Modelle unterscheiden sich durch die Multiplikation mit dem $±1$–Spreizsignal $c(t)$ bei Sender und Empfänger, wobei von $c(t)$ lediglich der Spreizgrad $J$ bekannt ist.
Zu untersuchen ist, ob sich das untere BPSK–Modell auch bei PN–Modulation anwenden lässt und ob die BPSK–Fehlerwahrscheinlichkeit
- $$p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt { {2 \cdot E_{\rm B}}/{N_{\rm 0}} } \hspace{0.05cm} \right )$$
auch für die PN–Modulation gültig ist, bzw. wie die angegebene Gleichung zu modifizieren ist.
Hinweise:
- Die Aufgabe gehört zum Kapitel PN–Modulation.
- Für die Lösung dieser Aufgabe ist die Angabe der spezifischen Spreizfolge (M–Sequenz oder Walsh–Funktion) nicht von Bedeutung.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
2. Richtig ist wieder der letzte Lösungsvorschlag. Im rauschfreien Fall ⇒ $n(t) = 0$ kann auf die zweifache Multiplikation mit $c(t)$ ∈ {+1, –1} verzichtet werden, so dass das obere Modell mit dem unteren Modell identisch ist.
3. Da beide Modelle im rauschfreien Fall identisch sind, muss nur das Rauschsignal angepasst werden: $n'(t) = n(t) · c(t)$. Die Lösungsvorschläge 2 und 3 sind dagegen nicht zutreffend: Die Integration muss weiterhin über $T = J · T_c$ erfolgen und die PN–Modulation verringert das AWGN–Rauschen nicht.
4. Multipliziert man das AWGN–Rauschen mit dem hochfrequenten ±1–Signal $c(t)$, so ist das Rauschen ebenfalls gaußförmig und weiß. Wegen $E[c^2(t)] = 1$ wird auch die Rauschvarianz nicht verändert. Die für BPSK gültige Gleichung $$p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt {{2 E_{\rm B}}/{N_{\rm 0}} } \hspace{0.05cm} \right )$$ ist somit auch bei der PN–Modulation anwendbar und zwar unabhängig vom Spreizfaktor J und von der spezifischen Spreizfolge. Bei AWGN–Rauschen wird die Fehlerwahrscheinlichkeit durch Bandspreizung weder vergrößert noch verkleinert. Richtig ist also der letzte Lösungsvorschlag.