Difference between revisions of "Aufgaben:Exercise 4.06: Optimal Decision Boundaries"
| Line 2: | Line 2: | ||
{{quiz-Header|Buchseite=Digitalsignalübertragung/Approximation der Fehlerwahrscheinlichkeit}} | {{quiz-Header|Buchseite=Digitalsignalübertragung/Approximation der Fehlerwahrscheinlichkeit}} | ||
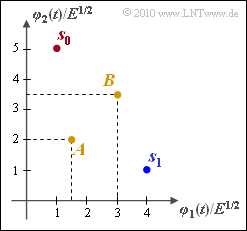
| + | [[File:P_ID2015__Dig_A_4_6.png|right|frame|Signalraumkonstellation für <i>N</i> = 2, <i>M</i> = 2]] | ||
| + | Wie betrachten ein binäres Nachrichtensystem ($M = 2$), das durch die gezeichnete 2D–Signalraumkonstellation ($N = 2$) festliegt. Für die beiden möglichen Sendevektoren, die mit den Nachrichten $m_0$ und $m_1$ direkt gekoppelt sind, gilt: | ||
| + | :$$\boldsymbol{ s }_0 \hspace{-0.1cm} \ =\ \hspace{-0.1cm} \sqrt {E} \cdot (1,\hspace{0.1cm} 5) \hspace{0.2cm} \Longleftrightarrow \hspace{0.2cm} m_0 \hspace{0.05cm},$$ | ||
| + | :$$ \boldsymbol{ s }_1 \hspace{-0.1cm} \ =\ \hspace{-0.1cm} \sqrt {E} \cdot (4, \hspace{0.1cm}1) \hspace{0.2cm} \Longleftrightarrow \hspace{0.2cm} m_1 \hspace{0.05cm}.$$ | ||
| − | [[ | + | Gesucht ist jeweils die optimale Entscheidungsgrenze zwischen den Regionen $I_0 ⇔ m_0$ und $I_1 ⇔ m_1$, wobei von folgenden Voraussetzungen ausgegangen wird: |
| + | * Für die Teilaufgaben (1) bis (3) gilt | ||
| + | :$${\rm Pr}(m_0 ) = {\rm Pr}(m_1 ) = 0.5 | ||
| + | \hspace{0.05cm}. $$ | ||
| + | * Für die Teilaufgaben (4) und (5) soll dagegen gelten: | ||
| + | :$${\rm Pr}(m_0 ) = 0.817 \hspace{0.05cm},\hspace{0.2cm} {\rm Pr}(m_1 ) = 0.183\hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm} {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_0)}{{\rm Pr}( m_1)} = | ||
| + | 1.5 | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | Bei AWGN–Rauschen mit der Varianz $\sigma_n^2$ ist die Entscheidungsgrenze die Lösung der folgenden vektoriellen Gleichung hinsichtlich des Vektors ($\rho_1, \rho_2$): | ||
| + | :$$|| \boldsymbol{ s }_1||^2 - || \boldsymbol{ s }_0||^2 + 2 \cdot \sigma_n^2 \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_0)}{{\rm Pr}( m_1)} = | ||
| + | 2 \cdot \boldsymbol{ \rho }^{\rm T} \cdot (\boldsymbol{ s }_1 - \boldsymbol{ s }_0)\hspace{0.05cm},\hspace{0.2cm} | ||
| + | \boldsymbol{ \rho } = (\rho_1 , \hspace{0.1cm}\rho_2 )\hspace{0.05cm}.$$ | ||
| + | |||
| + | Zusätzlich sind in der Grafik zwei Empfangswerte | ||
| + | :$$\boldsymbol{ A }= \sqrt {E} \cdot (1.5, \hspace{0.1cm}2)\hspace{0.05cm}, \hspace{0.2cm} \boldsymbol{ B }= \sqrt {E} \cdot (3, \hspace{0.1cm}3.5) $$ | ||
| + | |||
| + | eingezeichnet. Es ist zu überprüfen, ob diese bei den entsprechenden Randbedingungen den Regionen $I_0$ (und damit der Nachricht $m_0$) oder $I_1$ (Nachricht $m_1$) zugeordnet werden sollten. | ||
| + | |||
| + | ''Hinweise:'' | ||
| + | * Die Aufgabe bezieht sich auf das Kapitel [[Digitalsignal%C3%BCbertragung/Approximation_der_Fehlerwahrscheinlichkeit| Approximation der Fehlerwahrscheinlichkeit]] dieses Buches. Für numerische Berechnungen kann zur Vereinfachung die Energie $E = 1$ gesetzt werden. | ||
Revision as of 20:10, 6 November 2017
Wie betrachten ein binäres Nachrichtensystem ($M = 2$), das durch die gezeichnete 2D–Signalraumkonstellation ($N = 2$) festliegt. Für die beiden möglichen Sendevektoren, die mit den Nachrichten $m_0$ und $m_1$ direkt gekoppelt sind, gilt:
- $$\boldsymbol{ s }_0 \hspace{-0.1cm} \ =\ \hspace{-0.1cm} \sqrt {E} \cdot (1,\hspace{0.1cm} 5) \hspace{0.2cm} \Longleftrightarrow \hspace{0.2cm} m_0 \hspace{0.05cm},$$
- $$ \boldsymbol{ s }_1 \hspace{-0.1cm} \ =\ \hspace{-0.1cm} \sqrt {E} \cdot (4, \hspace{0.1cm}1) \hspace{0.2cm} \Longleftrightarrow \hspace{0.2cm} m_1 \hspace{0.05cm}.$$
Gesucht ist jeweils die optimale Entscheidungsgrenze zwischen den Regionen $I_0 ⇔ m_0$ und $I_1 ⇔ m_1$, wobei von folgenden Voraussetzungen ausgegangen wird:
- Für die Teilaufgaben (1) bis (3) gilt
- $${\rm Pr}(m_0 ) = {\rm Pr}(m_1 ) = 0.5 \hspace{0.05cm}. $$
- Für die Teilaufgaben (4) und (5) soll dagegen gelten:
- $${\rm Pr}(m_0 ) = 0.817 \hspace{0.05cm},\hspace{0.2cm} {\rm Pr}(m_1 ) = 0.183\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_0)}{{\rm Pr}( m_1)} = 1.5 \hspace{0.05cm}.$$
Bei AWGN–Rauschen mit der Varianz $\sigma_n^2$ ist die Entscheidungsgrenze die Lösung der folgenden vektoriellen Gleichung hinsichtlich des Vektors ($\rho_1, \rho_2$):
- $$|| \boldsymbol{ s }_1||^2 - || \boldsymbol{ s }_0||^2 + 2 \cdot \sigma_n^2 \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_0)}{{\rm Pr}( m_1)} = 2 \cdot \boldsymbol{ \rho }^{\rm T} \cdot (\boldsymbol{ s }_1 - \boldsymbol{ s }_0)\hspace{0.05cm},\hspace{0.2cm} \boldsymbol{ \rho } = (\rho_1 , \hspace{0.1cm}\rho_2 )\hspace{0.05cm}.$$
Zusätzlich sind in der Grafik zwei Empfangswerte
- $$\boldsymbol{ A }= \sqrt {E} \cdot (1.5, \hspace{0.1cm}2)\hspace{0.05cm}, \hspace{0.2cm} \boldsymbol{ B }= \sqrt {E} \cdot (3, \hspace{0.1cm}3.5) $$
eingezeichnet. Es ist zu überprüfen, ob diese bei den entsprechenden Randbedingungen den Regionen $I_0$ (und damit der Nachricht $m_0$) oder $I_1$ (Nachricht $m_1$) zugeordnet werden sollten.
Hinweise:
- Die Aufgabe bezieht sich auf das Kapitel Approximation der Fehlerwahrscheinlichkeit dieses Buches. Für numerische Berechnungen kann zur Vereinfachung die Energie $E = 1$ gesetzt werden.
Fragebogen
Musterlösung