Difference between revisions of "Aufgaben:Exercise 1.5: Cosine-Square Spectrum"
From LNTwww
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Digitalsignalübertragung/Eigenschaften von Nyquistsystemen }} [[File:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple…“) |
|||
| Line 4: | Line 4: | ||
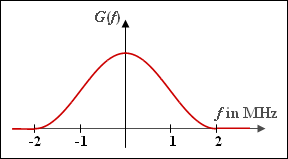
| − | [[File:|right|]] | + | [[File:P_ID1282__Dig_A_1_5.png|right|frame|Cosinus-Quadrat-Nyquistspektrum]] |
| + | Betrachtet wird das Spektrum $G(f)$ mit cos$^{2}$–förmigem Verlauf entsprechend der Skizze. Dieses erfüllt das erste Nyquistkriterium: | ||
| + | :$$\sum_{k = -\infty}^{+\infty} G(f - | ||
| + | \frac{k}{T} ) = {\rm const.}$$ | ||
| + | Dementsprechend hat der zugehörige Impuls $g(t)$ Nulldurchgänge bei Vielfachen von $T$, wobei $T$ noch zu bestimmen ist. Durch Fourierrücktransformation von $G(f)$ erhält man die Gleichung für den Zeitverlauf: | ||
| + | :$$g( t )= g_0 \cdot \frac{\cos(\pi \cdot t/T)}{1 - (2 \cdot | ||
| + | t/T)^2}\cdot {\rm si}(\pi \cdot {t}/{T})\hspace{0.05cm}.$$ | ||
| + | In den Fragen zu dieser Aufgabe werden auf folgende Eigenschaften Bezug genommen: | ||
| + | *Die hier betrachtete Spektralfunktion $G(f)$ ist ein Sonderfall des Cosinus–Rolloff–Spektrums, das punktsymmetrisch um die Nyquistfrequenz $f_{\rm Nyq}$ ist. | ||
| + | *Das Cosinus–Rolloff–Spektrum ist durch die Eckfrequenzen $f_{1}$ und $f_{2}$ vollständig gekennzeichnet. Für $| f | < f_{1}$ ist $G(f) = g_{0} \cdot T = const.$, während das Spektrum für $| f | > f_{2}$ keine Anteile besitzt. | ||
| + | *Der Zusammenhang zwischen der Nyquistfrequenz und den Eckfrequenzen lautet: | ||
| + | :$$f_{\rm Nyq}= \frac{f_1 +f_2 } | ||
| + | {2 }\hspace{0.05cm}.$$ | ||
| + | *Die Flankensteilheit wird durch den so genannten Rolloff–Faktor charakterisiert: | ||
| + | :$$r = \frac{f_2 -f_1 } | ||
| + | {f_2 +f_1 }\hspace{0.2cm}(0 \le r \le 1) \hspace{0.05cm}.$$ | ||
| + | ''Hinweis:'' | ||
| + | |||
| + | Diese Aufgabe bezieht sich auf die theoretischen Grundlagen von [[Digitalsignalübertragung/Eigenschaften_von_Nyquistsystemen|Eigenschaften von Nyquistsystemen]]. | ||
===Fragebogen=== | ===Fragebogen=== | ||
Revision as of 12:48, 5 November 2017
Betrachtet wird das Spektrum $G(f)$ mit cos$^{2}$–förmigem Verlauf entsprechend der Skizze. Dieses erfüllt das erste Nyquistkriterium:
- $$\sum_{k = -\infty}^{+\infty} G(f - \frac{k}{T} ) = {\rm const.}$$
Dementsprechend hat der zugehörige Impuls $g(t)$ Nulldurchgänge bei Vielfachen von $T$, wobei $T$ noch zu bestimmen ist. Durch Fourierrücktransformation von $G(f)$ erhält man die Gleichung für den Zeitverlauf:
- $$g( t )= g_0 \cdot \frac{\cos(\pi \cdot t/T)}{1 - (2 \cdot t/T)^2}\cdot {\rm si}(\pi \cdot {t}/{T})\hspace{0.05cm}.$$
In den Fragen zu dieser Aufgabe werden auf folgende Eigenschaften Bezug genommen:
- Die hier betrachtete Spektralfunktion $G(f)$ ist ein Sonderfall des Cosinus–Rolloff–Spektrums, das punktsymmetrisch um die Nyquistfrequenz $f_{\rm Nyq}$ ist.
- Das Cosinus–Rolloff–Spektrum ist durch die Eckfrequenzen $f_{1}$ und $f_{2}$ vollständig gekennzeichnet. Für $| f | < f_{1}$ ist $G(f) = g_{0} \cdot T = const.$, während das Spektrum für $| f | > f_{2}$ keine Anteile besitzt.
- Der Zusammenhang zwischen der Nyquistfrequenz und den Eckfrequenzen lautet:
- $$f_{\rm Nyq}= \frac{f_1 +f_2 } {2 }\hspace{0.05cm}.$$
- Die Flankensteilheit wird durch den so genannten Rolloff–Faktor charakterisiert:
- $$r = \frac{f_2 -f_1 } {f_2 +f_1 }\hspace{0.2cm}(0 \le r \le 1) \hspace{0.05cm}.$$
Hinweis:
Diese Aufgabe bezieht sich auf die theoretischen Grundlagen von Eigenschaften von Nyquistsystemen.
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)
(6)