Difference between revisions of "Aufgaben:Exercise 3.3: Noise at Channel Equalization"
| Line 66: | Line 66: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)'''& | + | '''(1)''' Aus $10 \cdot {\rm lg} \rho_U = 14.8 {\rm dB}$ folgt $\rho_U = 10^{\rm 1.48} ≈ 30.2$ und weiter mit der angegebenen Gleichung: |
| − | + | :$$\sqrt{\rho_{\rm U}} = \frac{\ddot{o}(T_{\rm D})/2}{ \sigma_d}\hspace{0.3cm}\Rightarrow | |
| − | + | \hspace{0.3cm} \sigma_d = \frac{0.478 \cdot s_0/2}{ \sqrt{30.2}} | |
| − | + | \hspace{0.15cm}\underline { \approx 0.044 \cdot s_0 }\hspace{0.05cm}.$$ | |
| − | |||
| − | |||
| + | |||
| + | '''(2)''' Bei gleicher Fehlerwahrscheinlichkeit $\rho_U$ (und damit gleichem $\rho_U$) muss $\sigma_d$ genau den gleichen Wert besitzen wie unter Teilaufgabe a) berechnet, da auch die Augenöffnung gleich bleibt ⇒ $\sigma_d/s_0 \underline{= 0.044}.$ | ||
| + | |||
| + | |||
| + | '''(3)''' Entsprechend dem Angabenblatt gilt: | ||
| + | :$$\alpha^2 = \frac{N_0 \cdot f_{\rm G}}{\sqrt{2} \cdot \sigma_d^2} | ||
| + | = \frac{10^{-9} \cdot s_0^2 \cdot T \cdot f_{\rm G}}{\sqrt{2} | ||
| + | \cdot \sigma_d^2} = 10^{-9} \cdot \frac{ f_{\rm G} \cdot | ||
| + | T}{\sqrt{2} \cdot (\sigma_d/s_0)^2}$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} \alpha^2 = 10^{-9} \cdot \frac{ | ||
| + | 0.35}{\sqrt{2} \cdot 0.044^2} \approx 1.28 \cdot 10^{-7} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | In ${\rm dB}$ ausgedrückt erhält man somit | ||
| + | :$$20 \cdot {\rm lg}\hspace{0.1cm}\alpha = 10 \cdot {\rm lg}\hspace{0.1cm}\alpha^2 = | ||
| + | -70\,{\rm dB}\hspace{0.1cm}+\hspace{0.1cm}10 \cdot {\rm lg}\hspace{0.1cm}1.28\hspace{0.15cm}\underline { = | ||
| + | -68.9\,{\rm dB}} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(4)''' Beim System B ist wegen $H_E(f = 0) = 1$ der normierte Wert gleich $1$, das heißt, es ist $\Phi_{\rm dN}(f = 0) = N_0/2$. Dagegen ist bei System A dieser Wert aufgrund der Komponenten der frequenzunabhängigen Kabeldämpfung $\alpha$ um $1/\alpha^2$ größer: | ||
| + | :$${\rm System}\hspace{0.15cm}{\rm A:}\hspace{0.1cm}\frac{{\it \Phi}_{d{\rm N}}(f = 0)}{N_0/2} = \frac{1}{\alpha^2} \hspace{0.15cm}\underline {\approx 7.8 \cdot 10^{6}} \hspace{0.05cm}, $$ | ||
| + | :$${\rm System}\hspace{0.15cm}{\rm B:}\hspace{0.1cm}\frac{{\it \Phi}_{d{\rm N}}(f = 0)}{N_0/2} &\hspace{-0.15cm}\underline {= 1 }\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(5)''' $\Phi_{\rm dN}(f)$ ist maximal, wenn der Exponent | ||
| + | :$$18.4 \cdot \sqrt{2 f T} - 2\pi \cdot \frac{(f \cdot T)^2}{0.49}$$ | ||
| + | |||
| + | den maximalen Wert besitzt. Mit $x = f \cdot T$ gilt somit für die Optimierungsfunktion: | ||
| + | :$$y(x) = 26.022 \cdot \sqrt{x} - 12.823 \cdot x^2 \approx 26 \cdot | ||
| + | \sqrt{x} - 13 \cdot x^2$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} \frac{{\rm d}y}{{\rm d}x} = \frac{26} | ||
| + | {2\cdot \sqrt{x}} - 13 \cdot 2 \cdot x = 0$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} \frac{1} { \sqrt{x}} = 2 \cdot x | ||
| + | \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\frac{1} { x} = 4 \cdot | ||
| + | x^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} x^3 = 0.25 | ||
| + | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} x \hspace{0.15cm}\underline {\approx 0.63} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | Damit ergibt sich $f_{\rm max} \cdot T$ näherungsweise zu $0.63$. | ||
| + | |||
| + | |||
| + | '''(6)''' Mit $x_{\rm max} = 0.63$ erhält man den Funktionswert | ||
| + | :$$y(x_{\rm max}) \approx 26 \cdot \sqrt{0.63} - 13 \cdot 0.63^2 | ||
| + | \hspace{0.15cm}\underline {\approx 15.477}.$$ | ||
| + | |||
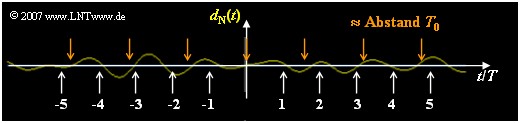
| + | Daraus folgt, dass die Rauschleistungsdichte bei der (normierten) Frequenz $f \cdot T \approx 0.63$ um den Faktor $e^{\rm 15.5} \underline{\approx 5.4 \cdot 10^6}$ größer ist als bei der Frequenz $f = 0$. Im Rauschanteil $d_N(t)$ überwiegen somit periodische Anteile mit der Periodendauer $T_0 \approx 1.6 \cdot T$. Die folgende Grafik zeigt eine Simulation und bestätigt dieses Ergebnis. | ||
| + | [[File:P_ID1408__Dig_A_3_3f.png]] | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 11:24, 24 October 2017
Wir betrachten zwei unterschiedliche Systemvarianten, die beide NRZ–Rechteck–Sendeimpulse benutzen und durch AWGN–Rauschen beeinträchtigt werden. In beiden Fällen wird zur Rauschleistungsbegrenzung ein Gaußtiefpass
- $$H_{\rm G}(f) = {\rm exp}(- \pi \cdot \frac{f^2}{(2f_{\rm G})^2})$$
mit der normierten Grenzfrequenz $f_G \cdot T = 0.35$ verwendet, so dass beide Systeme mit $\ddot{o}(T_D = 0) = 0.478 \cdot s_0$ auch die gleiche Augenöffnung aufweisen. Die pro Bit aufgewendete Sendeenergie $E_B = s_0^2 \cdot T$ ist um den Faktor $10^9$ größer als die Rauschleistungsdichte $N_0$ ⇒ $10\cdot {\rm lg} \, E_B/N_0 = 90 \, {\rm dB}$. Die beiden Systeme unterscheiden sich wie folgt.
- Der Kanalfrequenzgang von System A ist frequenzunabhängig: $H_K(f) = \alpha$. Für das Empfangsfilter ist demnach $H_E(f) = H_G(f)/\alpha$ anzusetzen, so dass für die Detektionsrauschleistung gilt:
- $$\sigma_d^2 = {N_0}/{2} \cdot \int_{-\infty}^{+\infty} |H_{\rm E}(f)|^2 \,{\rm d} f = \frac{N_0 \cdot f_{\rm G}}{\sqrt{2} \cdot \alpha^2} \hspace{0.05cm}.$$
- Dagegen ist für System B ein Koaxialkabel mit der charakteristischen Dämpfung (bei der halben Bitrate) $a_* = 80 \, {\rm dB}$ (bzw. $9.2 \, {\rm Np}$) vorausgesetzt, so dass für den Betragsfrequenzgang gilt:
- $$|H_{\rm K}(f)| = {\rm exp}(- 9.2 \hspace{0.05cm} \cdot \hspace{0.05cm}\sqrt{2 f T})\hspace{0.05cm}.$$
- Somit lautet die Gleichung für die Rauschleistungsdichte vor dem Entscheider (mit $f_G \cdot T = 0.35$):
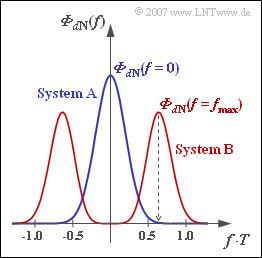
- $${\it \Phi}_{d{\rm N}}(f) = {N_0}/{2} \cdot \frac{|H_{\rm G }(f)|^2}{|H_{\rm K}(f)|^2} = {N_0}/{2} \cdot {\rm exp}\left [18.4 \cdot \sqrt{2 f T} - 2\pi \cdot \frac{(f \cdot T)^2}{(2 \cdot 0.35)^2} \right ] \hspace{0.05cm}.$$
Dieser Funktionsverlauf ist in obiger Grafik rot dargestellt. Die Rauchleistungsdichte für das System A ist blau gezeichnet.
Für das System B wurde messtechnisch die ungünstigste Fehlerwahrscheinlichkeit
- $$p_{\rm U} = {\rm Q} \left( \sqrt{\rho_{\rm U}} \right) \hspace{0.2cm}{\rm mit} \hspace{0.2cm} \rho_{\rm U} = \frac{[\ddot{o}(T_{\rm D})/2]^2}{ \sigma_d^2}$$
bestimmt. Die Messung ergab $p_U = 4 \cdot 10^{\rm -8}$, was dem Störabstand $10 \cdot {\rm lg} \, \rho_U = 14.8 \, {\rm dB}$ entspricht.
Hinweis: Die Aufgabe bezieht sich auf das Kapitel 3.3.
Fragebogen
Musterlösung
- $$\sqrt{\rho_{\rm U}} = \frac{\ddot{o}(T_{\rm D})/2}{ \sigma_d}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \sigma_d = \frac{0.478 \cdot s_0/2}{ \sqrt{30.2}} \hspace{0.15cm}\underline { \approx 0.044 \cdot s_0 }\hspace{0.05cm}.$$
(2) Bei gleicher Fehlerwahrscheinlichkeit $\rho_U$ (und damit gleichem $\rho_U$) muss $\sigma_d$ genau den gleichen Wert besitzen wie unter Teilaufgabe a) berechnet, da auch die Augenöffnung gleich bleibt ⇒ $\sigma_d/s_0 \underline{= 0.044}.$
(3) Entsprechend dem Angabenblatt gilt:
- $$\alpha^2 = \frac{N_0 \cdot f_{\rm G}}{\sqrt{2} \cdot \sigma_d^2} = \frac{10^{-9} \cdot s_0^2 \cdot T \cdot f_{\rm G}}{\sqrt{2} \cdot \sigma_d^2} = 10^{-9} \cdot \frac{ f_{\rm G} \cdot T}{\sqrt{2} \cdot (\sigma_d/s_0)^2}$$
- $$\Rightarrow \hspace{0.3cm} \alpha^2 = 10^{-9} \cdot \frac{ 0.35}{\sqrt{2} \cdot 0.044^2} \approx 1.28 \cdot 10^{-7} \hspace{0.05cm}.$$
In ${\rm dB}$ ausgedrückt erhält man somit
- $$20 \cdot {\rm lg}\hspace{0.1cm}\alpha = 10 \cdot {\rm lg}\hspace{0.1cm}\alpha^2 = -70\,{\rm dB}\hspace{0.1cm}+\hspace{0.1cm}10 \cdot {\rm lg}\hspace{0.1cm}1.28\hspace{0.15cm}\underline { = -68.9\,{\rm dB}} \hspace{0.05cm}.$$
(4) Beim System B ist wegen $H_E(f = 0) = 1$ der normierte Wert gleich $1$, das heißt, es ist $\Phi_{\rm dN}(f = 0) = N_0/2$. Dagegen ist bei System A dieser Wert aufgrund der Komponenten der frequenzunabhängigen Kabeldämpfung $\alpha$ um $1/\alpha^2$ größer:
- $${\rm System}\hspace{0.15cm}{\rm A:}\hspace{0.1cm}\frac{{\it \Phi}_{d{\rm N}}(f = 0)}{N_0/2} = \frac{1}{\alpha^2} \hspace{0.15cm}\underline {\approx 7.8 \cdot 10^{6}} \hspace{0.05cm}, $$
- $${\rm System}\hspace{0.15cm}{\rm B:}\hspace{0.1cm}\frac{{\it \Phi}_{d{\rm N}}(f = 0)}{N_0/2} &\hspace{-0.15cm}\underline {= 1 }\hspace{0.05cm}.$$
(5) $\Phi_{\rm dN}(f)$ ist maximal, wenn der Exponent
- $$18.4 \cdot \sqrt{2 f T} - 2\pi \cdot \frac{(f \cdot T)^2}{0.49}$$
den maximalen Wert besitzt. Mit $x = f \cdot T$ gilt somit für die Optimierungsfunktion:
- $$y(x) = 26.022 \cdot \sqrt{x} - 12.823 \cdot x^2 \approx 26 \cdot \sqrt{x} - 13 \cdot x^2$$
- $$\Rightarrow \hspace{0.3cm} \frac{{\rm d}y}{{\rm d}x} = \frac{26} {2\cdot \sqrt{x}} - 13 \cdot 2 \cdot x = 0$$
- $$\Rightarrow \hspace{0.3cm} \frac{1} { \sqrt{x}} = 2 \cdot x \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\frac{1} { x} = 4 \cdot x^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} x^3 = 0.25 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} x \hspace{0.15cm}\underline {\approx 0.63} \hspace{0.05cm}.$$
Damit ergibt sich $f_{\rm max} \cdot T$ näherungsweise zu $0.63$.
(6) Mit $x_{\rm max} = 0.63$ erhält man den Funktionswert
- $$y(x_{\rm max}) \approx 26 \cdot \sqrt{0.63} - 13 \cdot 0.63^2 \hspace{0.15cm}\underline {\approx 15.477}.$$
Daraus folgt, dass die Rauschleistungsdichte bei der (normierten) Frequenz $f \cdot T \approx 0.63$ um den Faktor $e^{\rm 15.5} \underline{\approx 5.4 \cdot 10^6}$ größer ist als bei der Frequenz $f = 0$. Im Rauschanteil $d_N(t)$ überwiegen somit periodische Anteile mit der Periodendauer $T_0 \approx 1.6 \cdot T$. Die folgende Grafik zeigt eine Simulation und bestätigt dieses Ergebnis.