Difference between revisions of "Aufgaben:Exercise 3.11: Viterbi Receiver and Trellis Diagram"
| Line 3: | Line 3: | ||
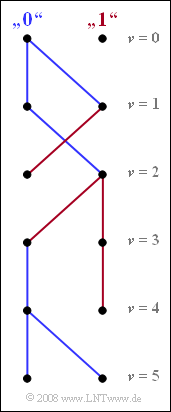
[[File:P_ID1475__Dig_A_3_11.png|right|frame|Trellisdiagramm für einen Vorläufer]] | [[File:P_ID1475__Dig_A_3_11.png|right|frame|Trellisdiagramm für einen Vorläufer]] | ||
| − | Der | + | Der Viterbi–Empfänger erlaubt eine aufwandsgünstige Realisierung der Maximum–Likelihood–Entscheidungsregel. Er beinhaltet die im Folgenden aufgeführten Systemkomponenten: |
| − | * ein an den Sendegrundimpuls angepasse Matched–Filter mit | + | * ein an den Sendegrundimpuls angepasse Matched–Filter mit Frequenzgang $H_{\rm MF}(f)$ und Ausgangssignal $m(t)$, |
* einen Abtaster im Abstand der Symboldauer (Bitdauer) $T$, der das zeitkontinuierliche Signal $m(t)$ in die zeitdiskrete Folge $〈m_{\rm \nu}〉$ wandelt, | * einen Abtaster im Abstand der Symboldauer (Bitdauer) $T$, der das zeitkontinuierliche Signal $m(t)$ in die zeitdiskrete Folge $〈m_{\rm \nu}〉$ wandelt, | ||
| − | * ein Dekorrelationsfilter mit | + | * ein Dekorrelationsfilter mit Frequenzgang $H_{\rm DF}(f)$ zur Entfernung statistischer Bindungen zwischen den Störanteilen der Folge $〈d_{\rm \nu}〉$, |
| − | * den Viterbi–Entscheider, der mit einem trellisbasierten Algorithmus die Sinkensymbolfolge $〈 | + | * den Viterbi–Entscheider, der mit einem trellisbasierten Algorithmus die Sinkensymbolfolge $〈v_{\rm \nu}〉$ gewinnt. |
| − | Die Grafik zeigt das vereinfachte Trellisdiagramm der beiden Zustände „$0$” und „$1$” für die Zeitpunkte $\nu ≤ 5$. Dieses Diagramm erhält man als Ergebnis der Auswertung der beiden minimalen Gesamtfehlergrößen ${\it \Gamma}_{\rm \nu}(0)$ und ${\it \Gamma}_{\rm \nu}(1)$ entsprechend der [ | + | Die Grafik zeigt das vereinfachte Trellisdiagramm der beiden Zustände „$0$” und „$1$” für die Zeitpunkte $\nu ≤ 5$. Dieses Diagramm erhält man als Ergebnis der Auswertung der beiden minimalen Gesamtfehlergrößen ${\it \Gamma}_{\rm \nu}(0)$ und ${\it \Gamma}_{\rm \nu}(1)$ entsprechend der [[Aufgaben:3.11Z_Maximum-Likelihood-Fehlergrößen| Aufgabe 3.11Z]]. |
| − | |||
| − | |||
| − | |||
| − | ''Hinweise:'' | + | |
| − | * Die Aufgabe gehört zum | + | ''Hinweise:'' |
| − | * Alle Größen sind hier normiert zu verstehen. | + | *Die Aufgabe gehört zum Kapitel [[Digitalsignal%C3%BCbertragung/Viterbi%E2%80%93Empf%C3%A4nger|Viterbi–Empfänger]]. |
| − | * Die hier angesprochene Thematik wird auch im | + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. |
| + | * Alle Größen sind hier normiert zu verstehen. Gehen Sie izudem von unipolaren und gleichwahrscheinlichen Amplitudenkoeffizienten aus: ${\rm Pr} (a_\nu = 0) = {\rm Pr} (a_\nu = 1)= 0.5.$ | ||
| + | * Die hier angesprochene Thematik wird auch im Interaktionsmodul [[Eigenschaften des Viterbi–Empfängers]] behandelt. | ||
Revision as of 13:42, 3 November 2017
Der Viterbi–Empfänger erlaubt eine aufwandsgünstige Realisierung der Maximum–Likelihood–Entscheidungsregel. Er beinhaltet die im Folgenden aufgeführten Systemkomponenten:
- ein an den Sendegrundimpuls angepasse Matched–Filter mit Frequenzgang $H_{\rm MF}(f)$ und Ausgangssignal $m(t)$,
- einen Abtaster im Abstand der Symboldauer (Bitdauer) $T$, der das zeitkontinuierliche Signal $m(t)$ in die zeitdiskrete Folge $〈m_{\rm \nu}〉$ wandelt,
- ein Dekorrelationsfilter mit Frequenzgang $H_{\rm DF}(f)$ zur Entfernung statistischer Bindungen zwischen den Störanteilen der Folge $〈d_{\rm \nu}〉$,
- den Viterbi–Entscheider, der mit einem trellisbasierten Algorithmus die Sinkensymbolfolge $〈v_{\rm \nu}〉$ gewinnt.
Die Grafik zeigt das vereinfachte Trellisdiagramm der beiden Zustände „$0$” und „$1$” für die Zeitpunkte $\nu ≤ 5$. Dieses Diagramm erhält man als Ergebnis der Auswertung der beiden minimalen Gesamtfehlergrößen ${\it \Gamma}_{\rm \nu}(0)$ und ${\it \Gamma}_{\rm \nu}(1)$ entsprechend der Aufgabe 3.11Z.
Hinweise:
- Die Aufgabe gehört zum Kapitel Viterbi–Empfänger.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Alle Größen sind hier normiert zu verstehen. Gehen Sie izudem von unipolaren und gleichwahrscheinlichen Amplitudenkoeffizienten aus: ${\rm Pr} (a_\nu = 0) = {\rm Pr} (a_\nu = 1)= 0.5.$
- Die hier angesprochene Thematik wird auch im Interaktionsmodul Eigenschaften des Viterbi–Empfängers behandelt.
Fragebogen
Musterlösung
(2) Die beiden bei $\underline {\nu = 1}$ ankommenden Pfeile sind jeweils blau gezeichnet und kennzeichnen das Symbol $a_1 = 0$. Somit ist bereits zu diesem Zeitpunkt das Ausgangssymbol $a_1$ festgelegt. Ebenso stehen die Symbole $a_3 = 1$ und $a_5 = 0$ bereits zu den Zeitpunkten $\underline {\nu = 3}$ bzw. $\underline {\nu = 5}$ fest.
Dagegen ist zum Zeitpunkt $\nu = 2$ eine Entscheidung bezüglich des Symbols $a_2$ nicht möglich. Unter der Hypothese, dass das nachfolgende Symbol $a_3 = 0$ sein wird, würde sich Symbol $a_2 = 1$ ergeben (bei „$0$” kommt ein roter Pfad an, also von „$1$” kommend). Dagegen führt die Hypothese $a_3 = 1$ zum Ergebnis $a_2 = 0$ (der bei „$1$” ankommende Pfad ist blau).
(3) Aus den durchgehenden Pfaden bei $\nu = 5$ ist ersichtlich:
- $$a_{1}\hspace{0.15cm}\underline {=0} \hspace{0.05cm},\hspace{0.2cm} a_{2}\hspace{0.15cm}\underline { =0} \hspace{0.05cm},\hspace{0.2cm}a_{3}\hspace{0.15cm}\underline {=1} \hspace{0.05cm},\hspace{0.2cm} a_{4}\hspace{0.15cm}\underline {=0} \hspace{0.05cm},\hspace{0.2cm} a_{5}\hspace{0.15cm}\underline {=0} \hspace{0.05cm}.$$
(4) Richtig ist nur die zweite Aussage: Da die Quellensymbole „$0$” und „$1$” als gleichwahrscheinlich vorausgesetzt wurden, ist der ML–Empfänger (Viterbi) identisch mit dem MAP–Empfänger.
Ein Schwellenwertentscheider – der zu jedem Takt eine symbolweise Entscheidung trifft – hat nur dann die gleiche Fehlerwahrscheinlichkeit wie der Viterbi–Empfänger, wenn es keine Impulsinterferenzen gibt. Dies ist hier offensichtlich nicht der Fall, sonst müsste zu jedem Zeitpunkt $\nu$ eine endgültige Entscheidung getroffen werden können.
Die erste Aussage trifft ebenfalls nicht zu. Das würde nämlich bedeuten, dass der Viterbi–Empfänger die Fehlerwahrscheinlichkeit $0$ haben kann. Dies ist aus der informationstheoretischen Gründen nicht möglich.